DS博客作业03--树
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业03--树 |
| 这个作业的目标 | 学习树结构设计及运算操作 |
| 姓名 | 邓宏 |
0.PTA得分截图

1.本周学习总结(5分)
学习总结,请结合树的图形展开分析。
1.1 二叉树结构
1.1.1 二叉树的2种存储结构
顺序存储
借用数组将二叉树中的数据元素存储起来。此方式只适用于完全二叉树,如果想存储普通二叉树,需要将普通二叉树转化为完全二叉树。
使用数组存储完全二叉树时,从数组的起始地址开始,按层次顺序从左往右依次存储完全二叉树中的结点。当提取时,根据完全二叉树的第 2 条性质,可以将二叉树进行还原。
数组中存储为:
根据完全二叉树的第 2 条性质就可以根据数组中的数据重新搭建二叉树的结构。
如果普通二叉树也采取顺序存储的方式,就需要将其转化成完全二叉树,然后再存储,例如:
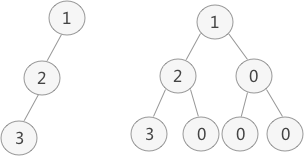
转化前 ~~~~~~~~~~~~转化后
链式存储
结点结构代码表示:
typedef struct BiTNode
{
TElemType data; //数据域
struct BiTNode *lchild, *rchild; //左右孩子指针
}BiTNode, *BiTree;
顺序存储时,相邻数据元素的存放地址也相邻(逻辑与物理统一);要求内存中可用存储单元的地址必须是连续的。
优点:存储密度大(=1),存储空间利用率高。
缺点:插入或删除元素时不方便。
链式存储时,相邻数据元素可随意存放,但所占存储空间分两部分,一部分存放结点值,另一部分存放表示结点间关系的指针
优点:插入或删除元素时很方便,使用灵活。
缺点:存储密度小(<1),存储空间利用率低。
1.1.2 二叉树的构造
最常用方法
void CreateBiTree(string str, BiTree& T, int index)
{
if (index > str.size()-1)
{
T = NULL;
return;
}
if (str[index] == '#')
{
T = NULL;
}
else
{
T = new BiTNode;
T->data = str[index];
CreateBiTree(str, T->lchild, 2 * index);
CreateBiTree(str, T->rchild, 2 * index + 1);
}
}
先序遍历建二叉树
BTree CreatTree(string str, int &i)
{
BTree bt;
if (i > len - 1) return NULL;
if (str[i] == '#') return NULL;
bt = new BTNode;
bt->data = str[i];
bt->lchild = CreatTree(str, ++i);
bt->rchild = CreatTree(str, ++i);
return bt;
}
已知二叉树先序遍历序列和中序遍历序列建二插树
node* BitryTree(char a[],char b[],int n){
node *T;
int i;
if(!n)
return NULL;即当先树遍历左子树为空时
else{
T = (node *)malloc(sizeof(struct node));
T->data = a[0];
for(i=0;i<n;i++)
{
if(a[0]==b[i])
break;
}
T->left = BitryTree(a+1,b,i);//先遍历左子树
T->right = BitryTree(a+1+i,b+i+1,n-i-1);
}
看法:
最常用第一种建树方法,但主要依具体情节选择合适方法
1.1.3 二叉树的遍历
总结二叉树的4种遍历方式,如何实现。
递归先序遍历二叉树
void PreOrderTraverse(BiTree & t)
{
if(t!=NULL)
{
cout<<t->data;
PreOrderTraverse(t->lchild);
PreOrderTraverse(t->rchild);
}
}
递归中序遍历二叉树
void InOrderTraverse(BiTree & t)
{
if(t!=NULL)
{
InOrderTraverse(t->lchild);
cout<<t->data;
InOrderTraverse(t->rchild);
}
}
递归后序遍历二叉树
void InOrderTraverse(BiTree & t)
{
if(t!=NULL)
{
InOrderTraverse(t->lchild);
InOrderTraverse(t->rchild);
cout<<t->data;
}
}
递归层次遍历二叉树
#include <queue>
void LevelOrder(BTNode* b)
{
BTNode* p;
SqQueue* qu;//定义唤醒队列指针
InitQueue(qu);//初始化队列
enQueue(qu, b);
while (!QueueEmply(qu))
{
deQueueEmpty(qu, p);
printf("%c", p->data);
if (p->lchild != NULL)
enQueue(qu, p->lchild);
if (p->rchild != NULL)
enQueue(qu, p->rchild);
}
DestroyQueue(qu);
}
1.1.4 线索二叉树
建立线索的规则:
(1)如果ptr->lchild为空,则存放指向中序遍历序列中该结点的前驱结点。这个结点称为ptr的中序前驱;
(2)如果ptr->rchild为空,则存放指向中序遍历序列中该结点的后继结点。这个结点称为ptr的中序后继;
声明:
typedef struct node
{
ElemType data;
int ltag, rtag; //增加的线索标记
struct node* lchild;
struct node* rchild;
}TBTNode; //线索二叉树中的节点类型
对二叉树p进行中序线索化
TBTNode* pre;//全局变量
void Thread(TBTNode*& p)
{
if (p != NULL)
{
Thread(p->lchild);//左子树线索化
if (p->lchild == NULL)//左孩子不存在,进行前驱结点线索化
{
p->lchild = pre;//建立当前结点的前驱结点线索
p->ltag = 1;
}
else//p结点的左子树已线索化
p->ltag = 0;
if (pre->rchild == NULL)//对pre的后继结点线索化
{
pre->rchild = p;//建立前驱结点的后继结点线索
pre->rtag = 1;
}
else
p->rtag = 0;
pre = p;
Thread(p->rchild);//右子树线索化
}
}
TBTNode* CreateThread(TBTNode* b)//中序线索化二叉树
{
TBTNode* root;
root = (TBTNode*)malloc(sizeof(TBTNode));//创建头结点
root->ltag = 0; root->rtag = 1;
root->rchild = b;
if (b == NULL)//空二叉树
root->lchild = root;
else
{
root->lchild = b;
pre = root;//pre是结点p的前驱结点,供加线索用
Thread(b);//中序遍历线索化二叉树
pre->rchild = root;//最后处理,加入指向头结点的线索
pre->rtag = 1;
root->rchild = pre;//头结点右线索化
}
return root;
}
1.1.5 二叉树的应用--表达式树
建
void InitExpTree(BTree& T, string str)//建表达式树
{
stack<BTree> s;//存放数字
stack<char> op;//存放运算符
op.push('#');
int i = 0;
while (str[i])//树结点赋值
{
if (!In(str[i]))//数字
{
T = new BiTNode;
T->data = str[i++];
T->lchild = T->rchild = NULL;
s.push(T);
}
else
{
switch (Precede(op.top(), str[i]))
{
case'<':
op.push(str[i]);
i++; break;
case'=':
op.pop();
i++; break;
case'>':
T = new BiTNode;
T->data = op.top();
T->rchild = s.top();
s.pop();
T->lchild = s.top();
s.pop();
s.push(T);
op.pop();
break;
}
}
}
while (op.pop() != '#')
{
T = new BiTNode;
T->data = op.top();
op.pop();
T->rchild = s.top();
s.pop();
T->lchild = s.top();
s.pop();s.push(T);
}
}
计算表达式树
double EvaluateExTree(BTree T)
{
double a, b;
if (T)
{
if (!T->lchild && !T->rchild)
return T->data - '0';
a = EvaluateExTree(T->lchild);
b = EvaluateExTree(T->rchild);
switch (T->data)
{
case'+': return a + b; break;
case'-': return a - b; break;
case'*': return a * b; break;
case'/':
if (b == 0)
{
cout << "divide 0 erroe!" << endl;
exit(0);
}
return a / b; break;
}
}
}
1.2 多叉树结构
1.2.1 多叉树结构
主要介绍孩子兄弟链结构
孩子兄弟表示法就是既表示出每个结点的第一个孩子结点,也表示出每个结点的下一个兄弟结点。孩子兄弟表示法需要为每个结点设计三个域:一个数据元素域、一个指向该结点的第一个孩子结点的指针域、一个指向该结点的下一个兄弟结点的指针域。
声明:
typedef struct TNode
{
ElemType data;//结点的值
struct TNode* hp;//指向兄弟结点
struct TNode* vp;//指向孩子结点
}TSBNode;//孩子兄弟链存储结构中的结点类型
1.2.2 多叉树遍历
void preorder(TR* T)
{
if (T)
{
cout << T->data << " ";
preorder(T->fir);
preorder(T->sib);
}
}
1.3 哈夫曼树
1.3.1 哈夫曼树定义
什么是哈夫曼树?,哈夫曼树解决什么问题?
哈夫曼树也叫最优二叉树哈夫曼树。给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
用途:
判别树:用于描述分类过程的二叉树。
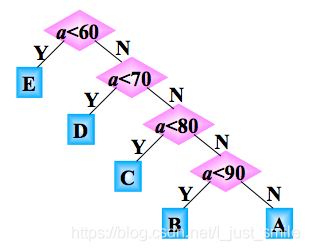
如果每次输入量都很大,那么应该考虑程序运行的时间。
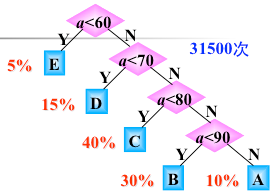
1.3.2 哈夫曼树的结构体
教材是顺序存储结构,也可以自己搜索资料研究哈夫曼的链式结构设计方式。
声明:
typedef struct
{
char data;//结点值
double weight;//权重
int parent;//双亲结点
int lchild, rchild;//左右孩子结点
}HTNode;
1.3.2 哈夫曼树构建及哈夫曼编码
void CreateHT(HTNode ht[], int n)
{
int i, k, lnode, rnode;
double min1, min2;
for (i = 1;i < 2 * n - 1;i++)//所有结点的相关域置初值-1
ht[i].parent = ht[i].lchild = ht[i].rchild = -1;
for (i = n;i <= 2 * n - 2;i++)//构造哈夫曼树的n-个分支结点
{
min1 = min2 = 32767;//lnode和rnode为最小权重的两个结点位置
lnode = rnode = -1;
for(k=0;k<=i-1;k++)//再ht[0...i-1]中找权值最小的两个结点
if (ht[k].parent==-1)//只在尚未构造二叉树的结点中查找
{
if (ht[k].weight < min1)
{
min2 = min1; rnode = lnode;
min1 = ht[k].weight;
lnode = k;
}
else if (ht[k].weight < min2)
{
min2 = ht[k].weight;
rnode = k;
}
}
ht[i].weight = ht[lnode].weight + ht[rnode].weight;
ht[i].lchild = lnode;
ht[i].rchild = rnode;//ht[i]作为双亲结点
ht[lnode].parent = i;
ht[rnode].parent = i;
}
}
void CreateHCode(HTNode ht[], HCode hcd[], int n)
{
int i, j, k;
HCode hc;
for (i = 0;i < n;i++)
{
hc.start = n;
k = i;
j = ht[i].parent;
while (j != -1)//循环至根结点
{
if (ht[j].lchild == k)
hc.cd[hc.start--] == '1';//当前结点时的双亲结点的左孩子
else
hc.cd[hc.start--] == '0';//当前结点时的双亲结点的右孩子
k = j; j = ht[j].parent;
}
hc.start++;//start指向哈夫曼编码最开始字符
hcd[i] = hc;
}
}
1.4 并查集
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中,其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。
优势:
并查集是若干个不相交集合,能够实现较快的合并和判断元素所在集合的操作,应用很多,如其求无向图的连通分量个数、最小公共祖先、带限制的作业排序,还有最完美的应用:实现Kruskar算法求最小生成树。
结构体
typedef struct
{
int data;//结点对应人的编号
int rank;//结点对应秩
int parent;//结点对应双亲下标
}UFSTree;//并查集树的结点类型
void MakeSet(UFSTree t[], int n)//初始化并查集树
{
int i;
for (i = 0;i < n;i++)
{
t[i].data = i;//数据为该人的编号
t[i].rank = 0;//秩初始化为0
t[i].parent = i;//双亲初始化为自己
}
}
查找
int FindSet(UFSTree t[], int x)//在并查集中查找集合编号
{
if (x != t[x].parent)//双亲不是自己
return (FindSet(t, t[x].parent));//递归在双亲中找x
else
return x;//双亲是自己,返回x
}
合并:
void UnionSet(UFSTree t[], int x, int y)//两个元素各自所属的集合的合并
{//将x和y所在的子树合并
x = FindSet(t, x);
y = FindSet(t, y);//查找x和y所在的分离集合树的编号
if (t[x].rank > t[y].rank)//y结点的秩小于x结点的秩
t[y].parent = x;//将y连接到x结点上,x作为y的双亲结点
else
{
t[x].parent = y;//将x连接到y结点上,y作为x的双亲结点
if (t[x].parent == t[y].parent)//x和y的秩相同
t[y].rank++;//y的秩加一
}
}
1.5.谈谈你对树的认识及学习体会。
树结构还是很有意思的,因为以前总是要写很多代码,现在到了树的结构,大多数都是直接用递归,代码量少(个别题目除外)。其实最主要的就是二叉树,不管是树还是森林,都可以转换成二叉树,在这个基础上进行操作,其中印象最深的的就是目录树了,虽然说操作起来有点麻烦,但是看到最终的结果还是十分有成就感的。但是结合之前知识点的题目又有点力不足的感觉,例如表达式树,究其原因应该是没有复习的锅了。树在生活中还是很多的,不仅仅是方便查找和存储数据,同时其中的哈夫曼树又可以用于数据的加密,涉及到一点密码学的内容,真的是很有意思了。
2.PTA实验作业(4分)
2.1 二叉树
2.1.1 解题思路及伪代码
运用递归先序创造树结构,将#作为递归出口,然后层次遍历输出
2.1.2 总结解题所用的知识点
1.递归先序创造树结构
2.层次遍历
2.2 目录树
2.2.1 解题思路及伪代码
主要思路:
1.定义结构体node,包含1)名字name(2)指向下级目录指针ctl(3)指向下级文件指针file(4)指向同级目录或文件指针next(取决于它本身是目录还是文件)。
定义一个全局的指针ptr,指向上一个处理完毕的结点,比如一开始在输入“a\b\c”的中,ptr一开始指向root,从root开始处理a,处理完后ptr指向a,然后从ptr(即a)开始处理b,处理完后ptr指向b,再从ptr(即b)开始处理c。
2.处理一行数据时,字符串后带\的为目录,否则为文件。
3.假设插入一个目录类型结点s,从某一结点(设为x)开始,如果x的目录为空,直接插入;如果不为空,从x的指向的目录a开始,s与a比较,如果小于(按字典序排在前面),则在x和a之间插入s即可,否则,s继续跟a的next结点b比较,如果s小于b了,则在a与b之间插入s,以此类推……如果到链表遍历完毕都没有找到比s大的结点,说明s最大,需要放在最后,在遍历结束后直接让链表最后一个结点指向s即可。在s插入完毕后,ptr指向s,表明下一个结点的处理是从ptr结点开始的,如本段开头s的插入是从x结点开始的。
如果s跟x的目录重名了,则不需要插入s,直接令ptr指向x即可,然后开始下一个结点的处理(那就是从x,即ptr开始处理了)。
4.假设插入一个文件类型结点s,方法与上述插入目录结点时类似,只是插入文件结点时,是小于(即按字典序规则排在前面),等于(即重名)的时候插入,因为当
文件重名时,不能说只有一个文件,有n个文件重名那就是有n个文件,所以s仍然需要插入,这里跟目录的插入不同,重名的目录即使有多个也是只看成一个的,所以不需要重复插入了。
5.还要注意,在a和c之间插入b时,需要分情况处理,如果a与b同级,是a的next指向b;如果a比高一级,则a的ctl或者file指针指向b。
2.2.2 总结解题所用的知识点
1.孩子兄弟链
2.后序遍历目录树,对每个结点的子目录和子文件进行排序
3.先序遍历进行输出。
3.阅读代码(0--1分)
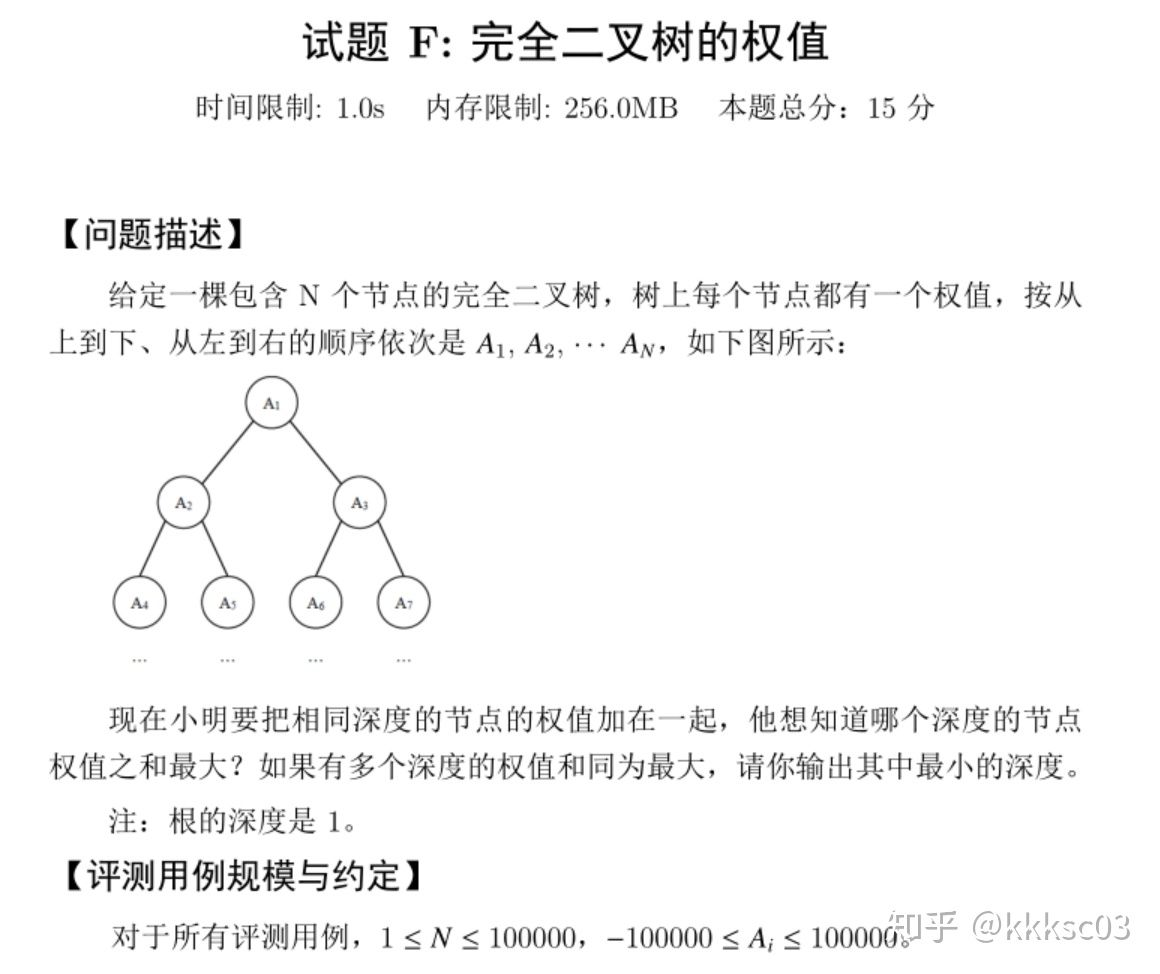
代码:
#include <iostream>
#include <cstdio>
using namespace std;
int main() {
long long n, maxnum = -3500000000ll, maxlayer, cnt = 0, flag = 0;
cin >> n;
for(int layer = 0; ; layer++) { // 枚举每一层,习惯上从 0 开始
long long sum = 0, a;
//cout << "<<" << (1 << layer) << endl;
for(int i = 0; i < (1 << layer); i++) { // 每一层的结点个数
cin >> a;
sum += a;
if(++cnt >= n) {
flag = 1;
break;
}
}
//cout << sum << endl;
if(sum > maxnum)
maxnum = sum, maxlayer = layer + 1;
if(flag) break;
}
cout << maxlayer;
return 0;
}
思路:
存储一个完全二叉树,可以使用一维数组存下所有结点。从上到下,从左到右,编号依次增加。可以发现,第一层有 1 个结点,第二层有 2 个,第三层有 4 个,第四层有 8 个……第 i 层有 [公式] 个结点。还可以发现,结点编号为 i 的话,它的左右子节点的编号分别是 2×i 和 2×i+1,不过这个和本题无关。
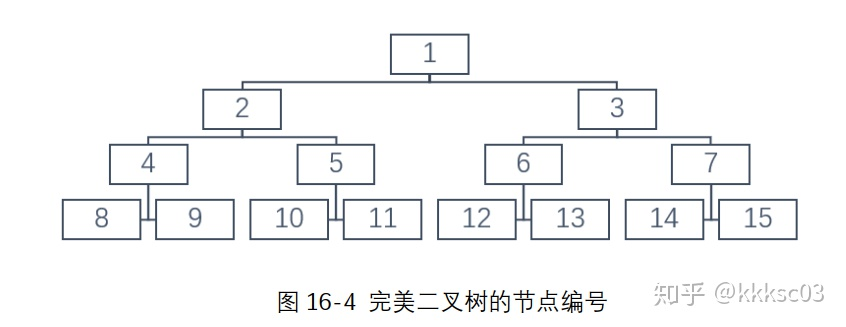
由于我们知道每一层的节点个数,可以直接输入数据后按层统计,甚至都可以不用数组把这些数字存下来。只要记录好读入的数字个数,在合适的时间退出循环就行。注意 << 符号是左移,1<<layer 的意思就是 [公式] 。如果读到的数字到了 n,那么就可以跳出循环,使用变量 flag 进行标记和判断。
本题有两个需要注意的地方
1.数据可能有小于 0 的,导致每层总和可能小于 0。
2.最多的一层可能有 100000-2^16 大约是 35000 个结点,所以要用 long long 防止总合爆 int。


