AtCoder Regular Contest 071 D - 井井井 / ###

 题目：http://arc071.contest.atcoder.jp/tasks/arc071_b

 

题意：

　　　　有一个二维的平面，给你xn根竖线和ym根横线，问这些线围成的长方形（正方形）的面积和（要求mod）。

　　　　例子：

　　　　　　3 3
　　　　　　1 3 4
　　　　　　1 3 6

　　　　

　　　　构成了9个长方体。

　　　　

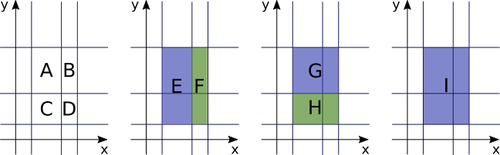
　　　　可以算出ans = 60；

 

题解：

　　　　　　　　很容易就可以想到暴击枚举 i,j,k,l，对应的每个值然后求面积。

　　　　　

 

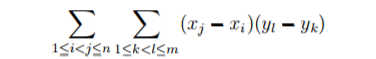
　　　　　　　　但是毫无疑问n4是会TLE的。

　　　　　　　　同样的答案等价于

　　　　

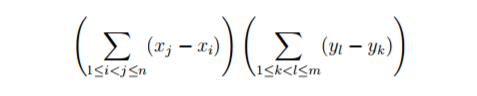
　　　　　　　　但是很不好意思，这样还是会TLE。

　　　　　　　　所以我们就可以把它化简为

　　　　　　　　

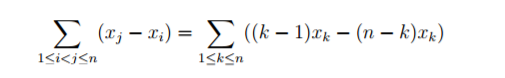
　　　　　　　————————————证明————————————

　　　　　　　　展开 ∑(xj-xi)为

　　　　　　　　(x2-x1)+(x3-x1)+····+(xn-x1)

　　　　　　　　(x3-x2)+(x4-x2)+···+（xn-x1）

　　　　　　　　···

　　　　　　　　不难发现当为第k个x的时候，在它前面有(k-1)个x要选择它，所以是 +（k-1）*xk 。而在k的后面有（n-k）个x。xk 要选它们，所以是 -（n-k）*xk 。

　　　　　　　　就可以化简成∑((k-1)xk-(n-k)xk)。把复杂度从n2降到n。

　　　　　　　　同理y也是这样。

　　　　　　　　总的复杂度为O(n+m)。

　　　　　　　——————————————————————————

 

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 #include <cstdlib>
 5 #include <string>
 6 #include <vector>
 7 #include <map>
 8 #include <set>
 9 #include <queue>
10 #include <sstream>
11 #include <algorithm>
12 using namespace std;
13 #define pb push_back
14 #define mp make_pair
15 #define ms(a, b)  memset((a), (b), sizeof(a))
16 //#define LOCAL
17 typedef long long LL;
18 const int inf = 0x3f3f3f3f;
19 const int maxn = 100000+10;
20 const int mod = 1e9+7;
21 LL x[maxn];
22 LL y[maxn];
23 int main()
24 {
25     #ifdef LOCAL
26         freopen("input.txt" , "r", stdin);
27     #endif // LOCAL
28     int n, m;
29     scanf("%d%d", &n, &m);
30     for(int i=1;i<=n;i++)   scanf("%lld", &x[i]);
31     for(int i=1;i<=m;i++)   scanf("%lld", &y[i]);
32     LL ans =0;
33     LL sumx = 0, sumy=0;
34     for(int i=1;i<=n;i++)
35         sumx =(sumx+ ( (i-1)*x[i] - (n-i)*x[i] )%mod)%mod;
36     for(int i=1;i<=m;i++)
37         sumy =(sumy+ ( (i-1)*y[i] - (m-i)*y[i] )%mod)%mod;
38 //    printf("%lld %lld\n", sumx, sumy);
39     printf("%lld\n", (sumx * sumy) %mod);
40     return 0;
41 }
View Code

 

posted @ 2017-04-10 23:51  Dh_q  阅读(181)  评论(0)  编辑  收藏  举报