Machine-Learning–Based Column Selection for Column Generation

论文阅读笔记，个人理解，如有错误请指正，感激不尽！仅是对文章进行梳理，细节请阅读参考文献。该文分类到Machine learning alongside optimization algorithms。

01 Column Generation

列生成 (Column Generation) 算法在组合优化领域有着非常广泛的应用，是一种求解大规模问题 (large-scale optimization problems) 的有效算法。在列生成算法中，将大规模线性规划问题分解为主问题 (Master Problem, MP) 和定价子问题 (Pricing Problem, PP)。算法首先将一个MP给restricted到只带少量的columns，得到RMP。求解RMP，得到dual solution，并将其传递给PP，随后求解PP得到相应的column将其加到RMP中。RMP和PP不断迭代求解直到再也找不到检验数为负的column，那么得到的RMP的最优解也是MP的最优解。如下图所示：

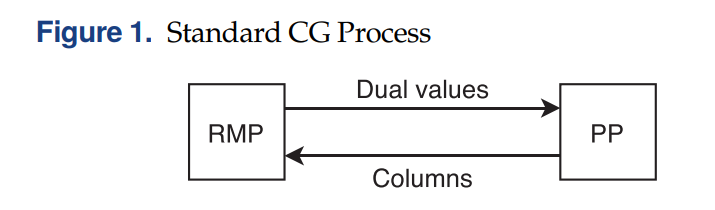
关于列生成的具体原理，之前已经写过很多详细的文章了。还不熟悉的小伙伴可以看看以下：

02 Column Selection

在列生成迭代的过程中，有很多技巧可以用来加快算法收敛的速度。其中一个就是在每次迭代的时候，加入多条检验数为负的column，这样可以减少迭代的次数，从而加快算法整体的运行时间。特别是求解一次子问题得到多条column和得到一条column相差的时间不大的情况下（例如，最短路中的labeling算法）。

而每次迭代中选择哪些column加入？是一个值得研究的地方。因为加入的columns不同，最终收敛的速度也大不一样。一方面，我们希望加入column以后，目标函数能尽可能降低（最小化问题）；另一方面，我们希望加入的column数目越少越好，太多的列会导致RMP求解难度上升。因此，在每次的迭代中，我们构建一个模型，用来选择一些比较promising的column加入到RMP中：

• Let \(\ell\) be the CG iteration number
• \(\Omega_{\ell}\) the set of columns present in the RMP at the start of iteration \(\ell\)
• \(\mathcal{G}_{\ell}\) the generated columns at this iteration
• For each column \(p \in \mathcal{G}_{\ell}\), we define a decision variable \(y_p\) that takes value one if column \(p\) is selected and zero otherwise

为了最小化所选择的column，每选择一条column的时候，都会发生一个足够小的惩罚\(\epsilon\)。最终，构建column selection的模型 (MILP) 如下：

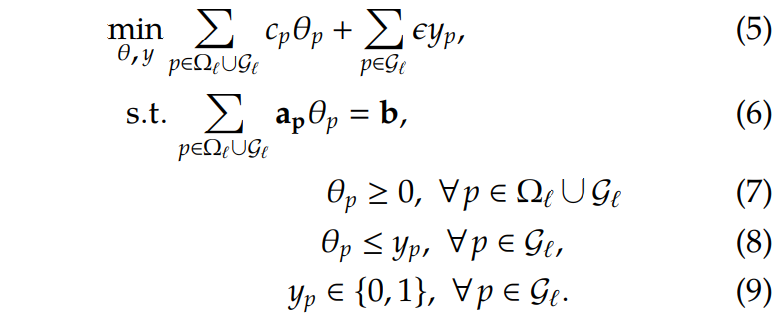
大家发现没有，如果没有\(y_p\)和约束(8)和(9)，那么上面这个模型就直接变成了下一次迭代的RMP了。

假设\(\epsilon\)足够小，这些约束目的是使得被选中添加到RMP中的column数量最小化，也就是这些\(y_p=1\)的columns。那么在迭代\(\ell\)中要添加到RMP的的column为：

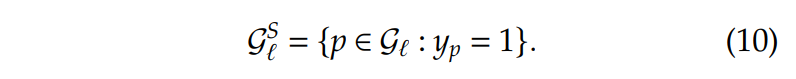
总体的流程如下图所示：

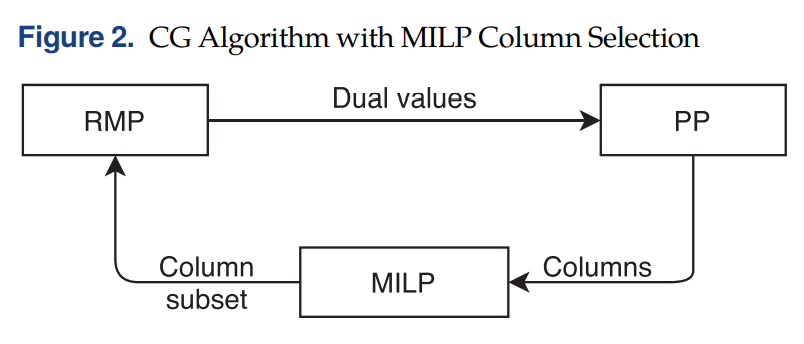
03 Graph Neural Networks

在每次迭代中，通过求解MILP，可以知道加入哪些column有助于算法速度的提高，但是求解MILP也需要一定的时间，最终不一定能达到加速的目的。因此通过机器学习的方法，学习一个MILP的模型，每次给出选中的column，将是一种比较可行的方法。

在此之前，先介绍一下Graph Neural Networks。图神经网络（GNNs）是通过图节点之间的信息传递来获取图的依赖性的连接模型。与标准神经网络不同，图神经网络可以以任意深度表示来自其邻域的信息。

给定一个网络\(G=(V,E)\)，其中\(V\)是顶点集而\(E\)是边集。每一个节点\(v \in V\)有着特征向量\(x_v\)。目的是迭代地aggregate（聚合）相邻节点的信息以更新节点的状态，令：

• \(h^{(k)}_v\) be the representation vector of node \(v \in V\)（注意和\(x_v\)区分开）at iteration \(k=0,1,...,K\)
• Let \(\mathcal{N}(v)\) be the set of neighbor (adjacent) nodes of \(v \in V\)

如下图所示，节点\(v_1\)从相邻节点\(v_2,v_3,v_4\) aggregate信息来更新自己：

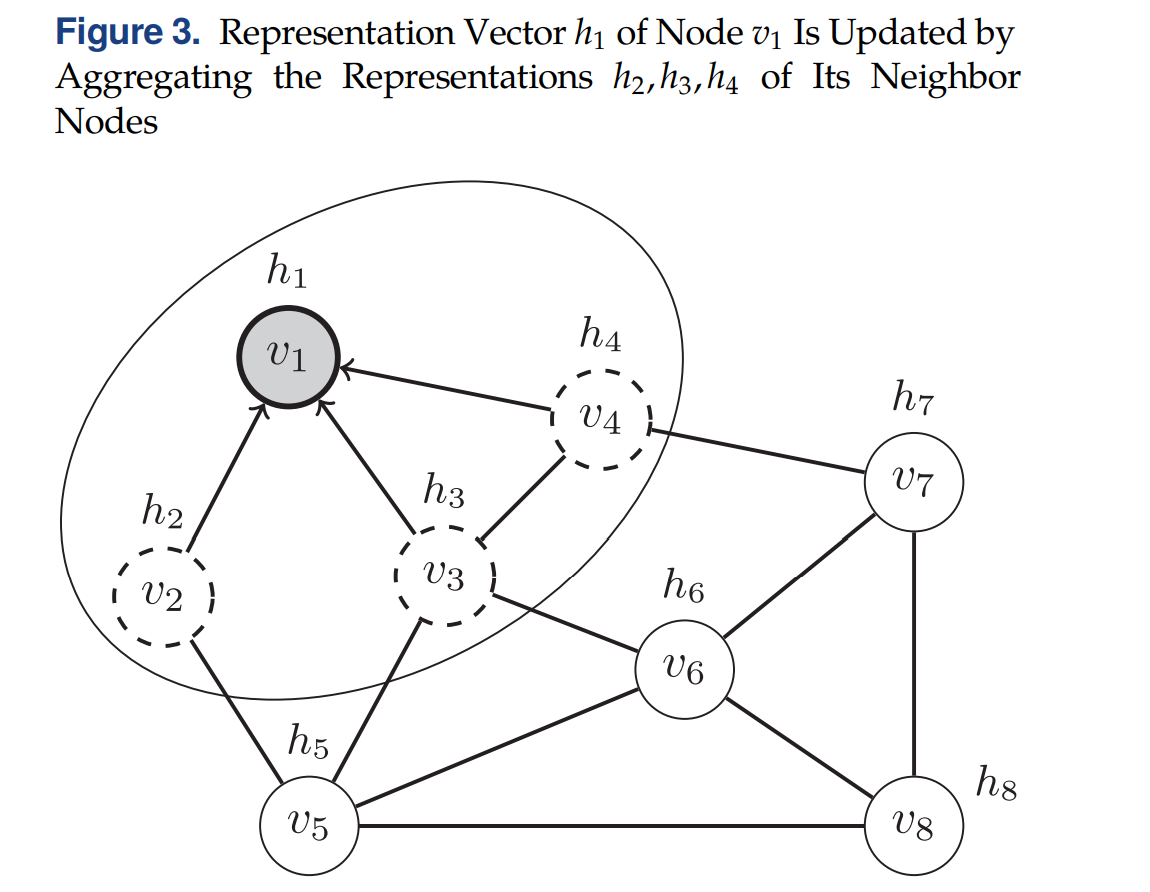
在迭代\(k > 0\)中，一个aggregated function，记为\(aggr\)，在每个节点\(v \in V\)上首先用于计算一个aggregated information vector \(a^{(k)}_v\):

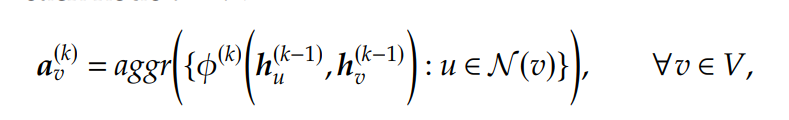
其中在初始时有\(h^{0}_v=x_v\)，\(\phi^{(k)}\)是一个学习函数。\(aggr\)应该和节点顺序无关，例如sum, mean, and min/max functions。

接着，使用另一个函数，记为\(comb\)，将aggregated information与节点当前的状态进行结合，更新后的节点representation vectors:

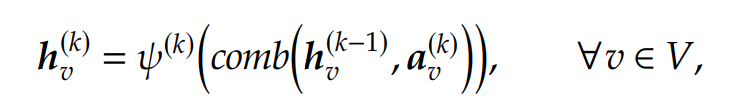
其中\(\psi^{(k)}\)是另一个学习函数。在不断的迭代中，每一个节点都收集来自更远邻居节点的信息，在最后的迭代\(K\)中，节点\(v \in V\)的 representation \(h^{(K)}_v\) 就可以用来预测其标签值\(l_v\)了，使用最后的转换函数（记为\(out\)），最终：

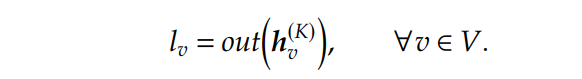
04 A Bipartite Graph for Column Selection

利用上面的GNN来做Column Selection，比较明显的做法是一个节点表示一个column，然后将两个column通过一条边连接如果他们都与某个约束相关联的话。但是这样会导致大量的边，并且对偶值的信息也很难在模型中进行表示。

因此作者使用了bipartite graph with two node types：column nodes \(V\) and constraint
nodes \(C\). An edge \((v, c)\) exists between a node \(v \in V\) and a node \(c \in C\) if column \(v\) contributes to constraint \(c\). 这样做的好处是可以在节点\(c\)上附加特征向量，例如对偶解的信息，如下图(a)所示：

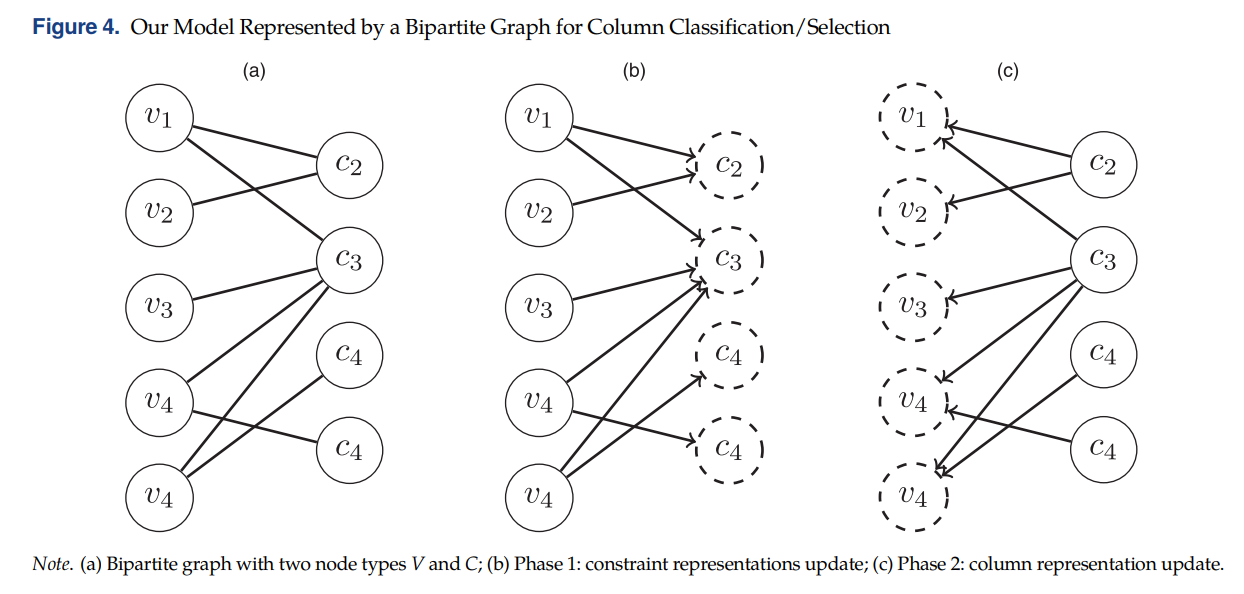
因为有两种类型的节点，每一次迭代时均有两阶段：阶段1更新Constraint节点\(c \in C\)(上图(b))，阶段2更新Column节点\(v \in V\)(上图(c))。最终，column节点的 representations \(h^{(K)}_v, v \in V\)被用来预测节点的labels \(y_v \in \{0, 1\}\)。算法的流程如下：

As described in the previous section, we start by initializing the representation vectors of both the column and constraint nodes by the feature vectors \(x_v\) and \(x_c\), respectively (steps 1 and 2). For each iteration \(k\), we perform the two phases: updating the constraint representations (steps 4 and 5), then the column ones (steps 6 and 7). The sum function is used for the aggr function and the vector concatenation for the comb function.

The functions \(\phi^{(k)}_C, \psi^{(k)}_C, \phi^{(k)}_V\), and \(\psi^{(k)}_V\) are two-layer feed forward neural networks with rectified linear unit (ReLU) activation functions and out is a three-layer feed forward neural network with a sigmoid function for producing the final probabilities (step 9).

A weighted binary cross entropy loss is used to evaluate the performance of the model, where the weights are used to deal with the imbalance between the two classes. Indeed, about 90% of the columns belong to the unselected class, that is, their label \(y_v = 0\).

05 数据采集

数据通过使用前面提到的MILP求解多个算例来采集column的labels。每次的列生成迭代都将构建一个Bipartite Graph并且存储以下的信息：

• The sets of column and constraint nodes;
• A sparse matrix \(E \in \mathbb{R}^{n\times m}\) storing the edges;
• A column feature matrix \(X^V \in \mathbb{R}^{n\times d}\), where \(n\) is the number of columns and d the number of column features;
• A constraint feature matrix \(X^C \in \mathbb{R}^{n\times p}\), where \(m\) is the number of constraints and \(p\) the number of constraint features;
• The label vector y of the newly generated
  columns in \(\mathcal{G}‘\).

06 Case Study I: Vehicle and Crew Scheduling Problem

关于这个问题的定义就不写了，大家可以自行去了解一下。

6.1 MILP Performance

通过刻画在列生成中使用MILP和不使用MILP(所有生成的检验数为负的column都丢进下一次的RMP里)的收敛图如下：

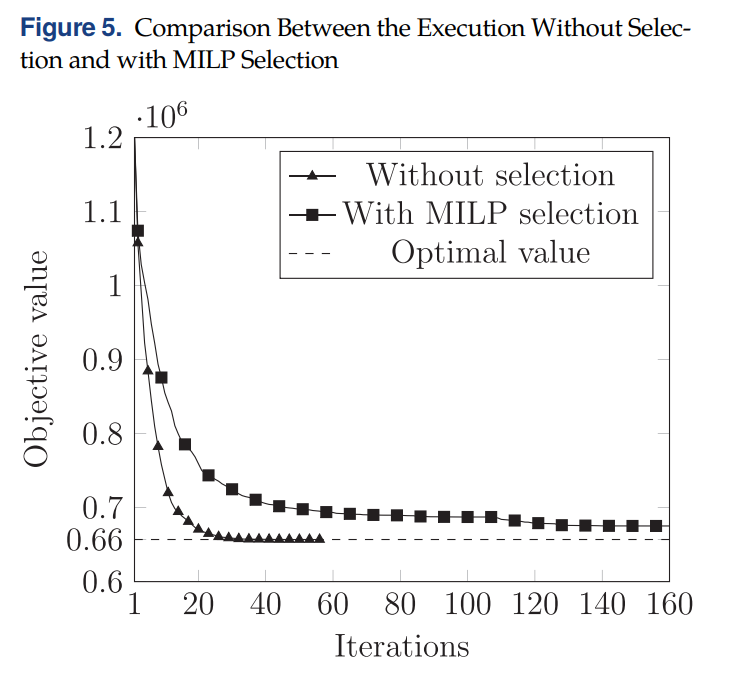
使用了MILP收敛速度反而有所下降，This is mainly due to the rejected columns that remain with a negative reduced cost after the RMP reoptimization and keep on being generated in subsequent iterations, even though they do not improve the objective value (degeneracy).

为了解决这个问题，一个可行的方法是运行MILP以后，额外再添加一些column。不过是先将MILP选出来的column加进RMP，进行求解，得到duals以后，再去未被选中的column中判断，哪些column在新的duals下检验数依然为负，然后进行添加。当然，未选中的column过多的话，不一定把所有的都加进去，按照检验数排序，加一部分就好（该文是50%）。如下图所示：

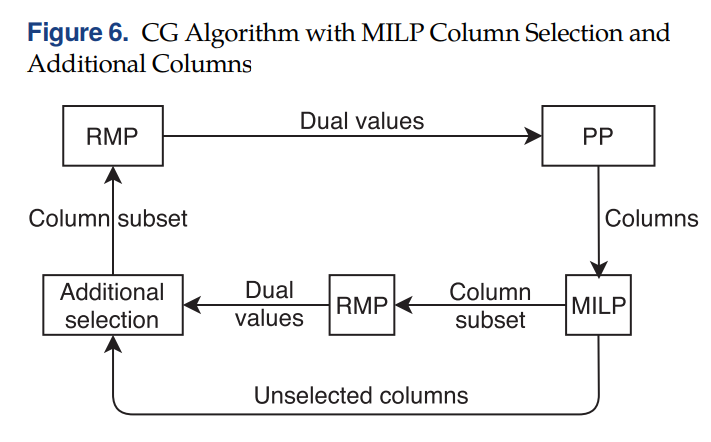
加入了额外的column以后，在进行preliminary的测试，结果如下(the computational time of the algorithm with column selection does not include the time spent solving the MILP at every iteration，因为作者只想了解selection对column generation的影响，反正MILP最后要被更快的GNN模型替代的。)：

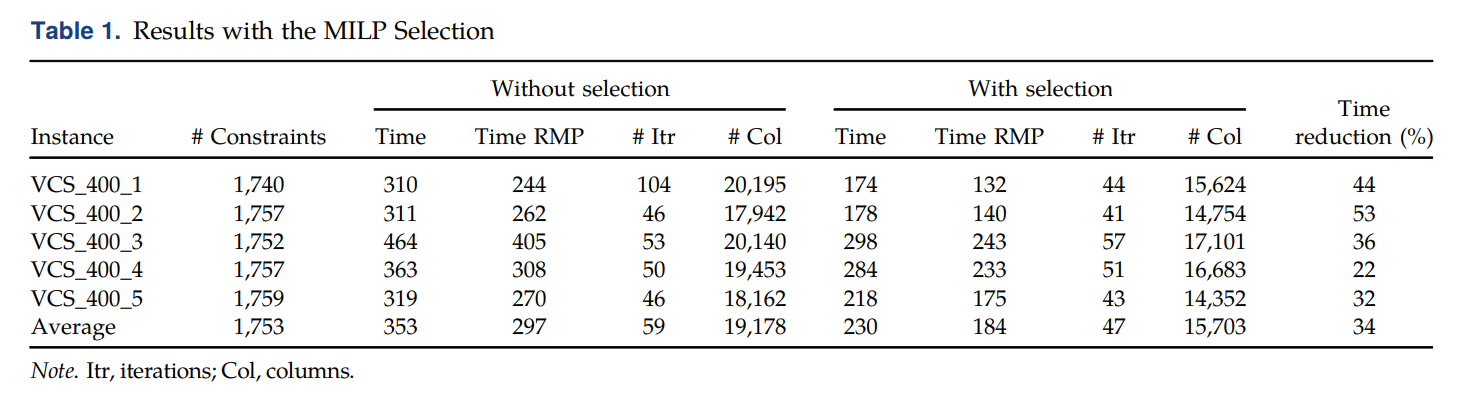
可以看到，MILP能节省更多的计算时间，减少约34%的总体时间。

6.2 Comparison

随后，对以下的策略进行对比：

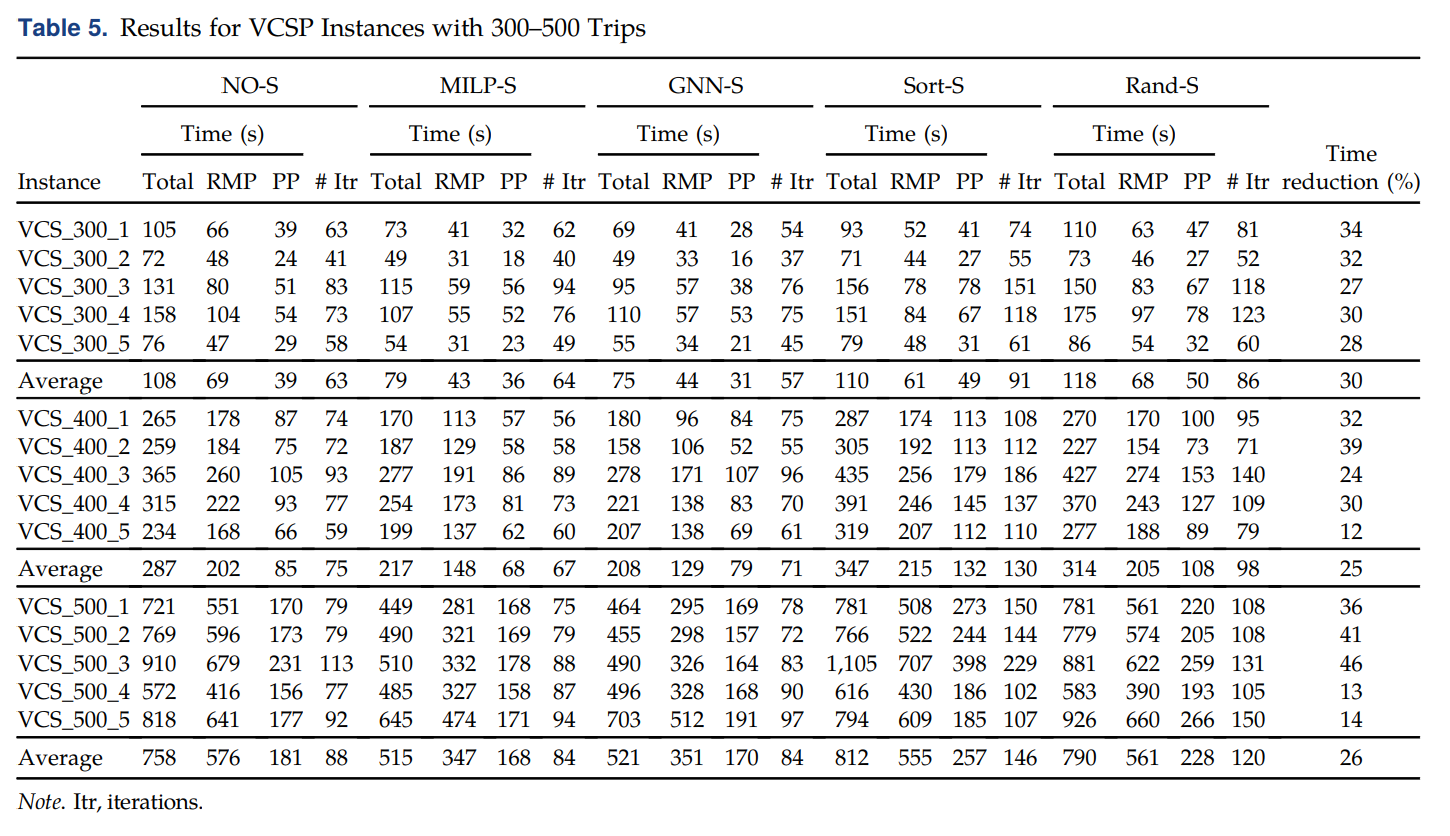
• No selection (NO-S): This is the standard CG algorithm with no selection involved, with the use of the acceleration strategies described in Section 2.
• MILP selection (MILP-S): The MILP is used to select the columns at each iteration, with 50% additional columns to avoid convergence issues. Because the MILP is considered to be the expert we want to learn from and we are looking to replace it with a fast approximation, the total computational time does not include the time spent solving the MILP.
• GNN selection (GNN-S): The learned model is used to select the columns. At every CG iteration, the column features are extracted, the predictions are obtained, and the selected columns are added to the RMP.
• Sorting selection (Sort-S): The generated columns are sorted by reduced cost in ascending order, and a subset of the columns with the lowest reduced cost are selected. The number of columns selected is on average the same as with the GNN selection.
• Random selection (Rand-S): A subset of the columns is selected randomly. The number of columns selected is on average the same as with the GNN selection

对比的结果如下，其中The time reduction column compares the GNN-S to the NO-S algorithm.相比平均减少26%的时间。

07 Case Study II: Vehicle Routing Problem with Time Windows

这是大家的老熟客了，就不过多介绍了。直接看对比的结果：

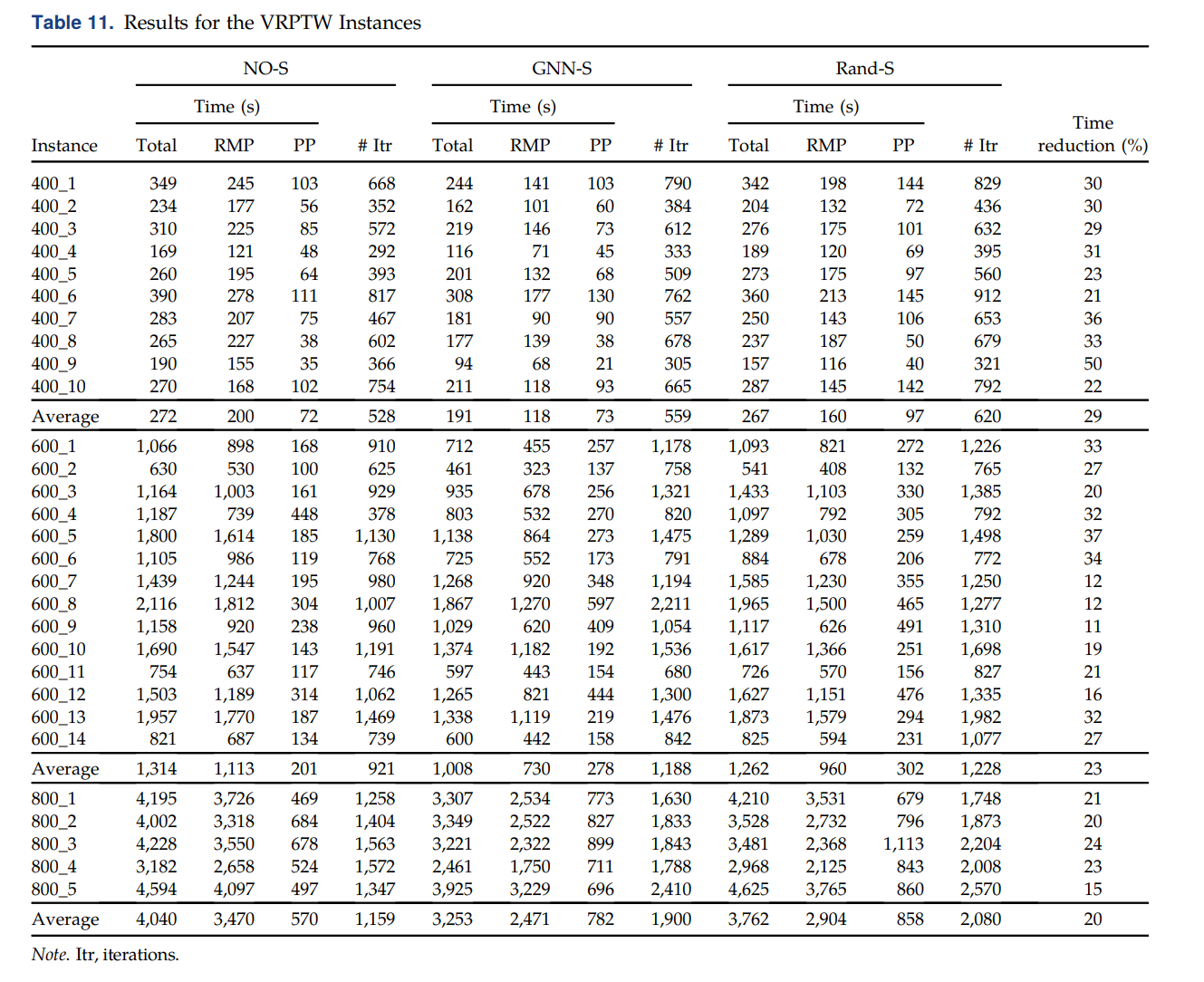
The last column corresponds to the time reduction when comparing GNN-S with NO-S. One can see that the column selection with the GNN model gives positive results, yielding average reductions ranging from 20%–29%. These reductions could have been larger if the number of CG iterations performed had not increased.

参考文献

• [1] Mouad Morabit, Guy Desaulniers, Andrea Lodi (2021) Machine-Learning–Based Column Selection for Column Generation. Transportation Science