帝国竞争算法(imperialist competitive algorithm, ICA )详解+Java代码实现
前言
这段时间用过这个算法做过相关的工作,今天就介绍一下吧。虽然感觉效果嘛,勉勉强强啦。不过每种算法肯定有其适用的地方,用到了就Mark一下方便后人吧~
介绍
帝国竞争算法(imperialist competitive algorithm,ICA)是Atashpaz-Gargari和Lucas于2007年提出的一种基于帝国主义殖民竞争机制的进化算法,属于社会启发的随机优化搜索方法。目前,ICA已被成功应用于多种优化问题中,如调度问题、分类问题和机械设计问题等。[2]
帝国主义竞争算法,借鉴了人类历史上政治社会殖民阶段帝国主义国家之间的竞争、占领、吞并殖民殖民地国家从而成为帝国国家的演化,是一种全局性的优化算法。该算法把所有初始化的个体都称作国家,按照国家势力分成帝国主义国家及殖民地两种,前者优势大于后者。[1]
其实,从另一个角度来看,ICA可以被认为是遗传算法(GA)的社会对应物。ICA是基于人类社会进化的过程,而GA是基于物种的生物进化过程。二者其实有异曲同工之妙。
不过话说回来,大多数群体仿生类算法都有异曲同工之妙~
流程图
学习算法框架,当然先搞懂流程图啦。算法的流程图我就不重新画了,找了一篇文献上的直接挪过来:[1]
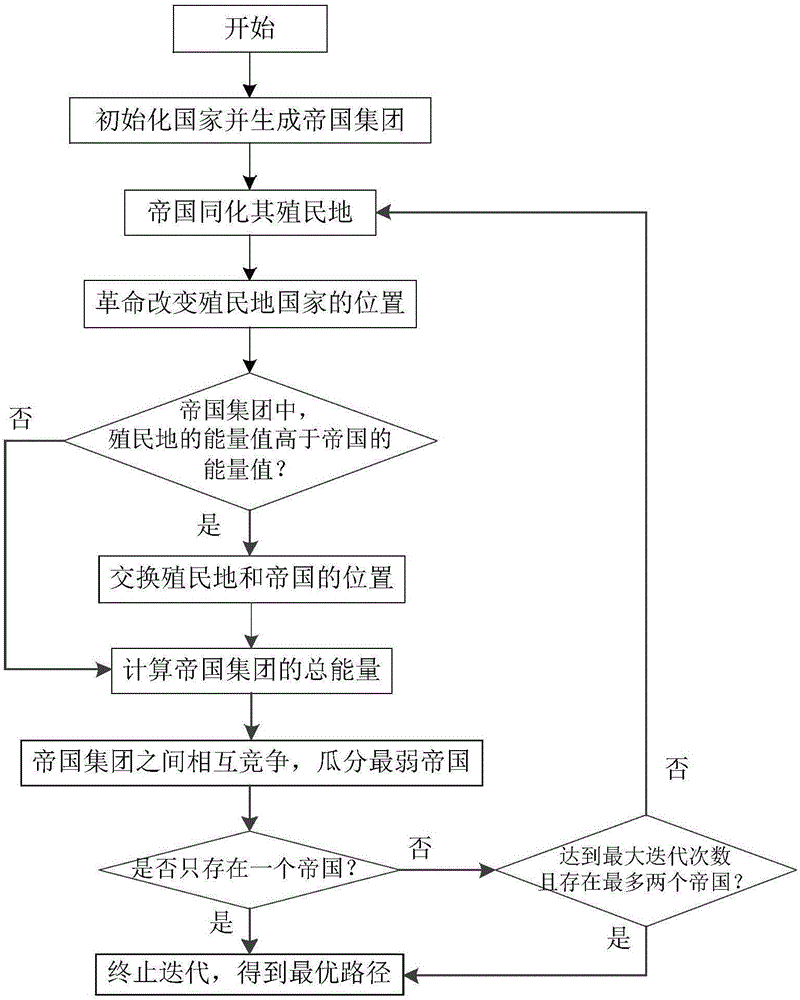
整个流程大体如上,可能大家在其他地方看到的有些专有名词可能对不上,但描述的都是一个东西,本质是一样的。我们下面来一步步分析这个过程吧。
算法解析
其实和群体进化类算法还是非常像的,只不过把个体的概念换成了国家而已。我们一步步来看。
1. 初始化
ICA的个体是国家,相当于遗传算法中的染色体,对于一个N维的优化问题,国家可以表示成如下形式:
国家的势力大小通过代价函数来衡量:
国家的势力和代价函数值成反比,即代价函数值越小,国家势力越大。初始帝国的产生分为以下几个步骤:
STEP 1:首先,随机产生$ N_{pop} \(个国家,从中选出势力较大的前\) N_{imp} \(个国家作为帝国主义国家,剩下的\) N_{col} $个国家作为殖民地。
STEP 2:其次,根据帝国主义国家的势力大小划分殖民地。每个帝国的殖民地个数按照式(1)~(3)计算:
其中,\(c_n\)是第$ n \(个帝国主义国家的代价函数值;\)C_n \(是它的标准化代价;\)p_n \(是它的标准化势力大小;\){ N.C. }{n}\(是第\) n \(个帝国的初始殖民地个数。最后,对于每个帝国主义国家,从\) N \(个殖民地中随机选择相应的个数分配给它,最终形成初始的\)N_{imp} $个帝国。[2]
不过这里解释一下,一个国家其实可以看成一个解的表示,与遗传中染色体类似。国家的势力通常由该国家所表示的解的好坏决定的。一般可以采用随机或者贪心的方式生成初始国家,然后计算目标函数,计算势力,再划分帝国主义国家和殖民地国即可。

2. 殖民地同化
帝国主义国家为了更好地控制其殖民地国家,将自己的思想模式及文化风俗推广到殖民地国家的过程,称为同化。ICA中通过所有殖民地向其所属帝国主义国家移动来模拟同化过程。[2] 当然这个移动可以看出解在解空间上的移动,与邻域搜索那个移动也有点类似,本质还是解的变换。
一个同化的例子如下,其实跟GA中的交叉很相似:
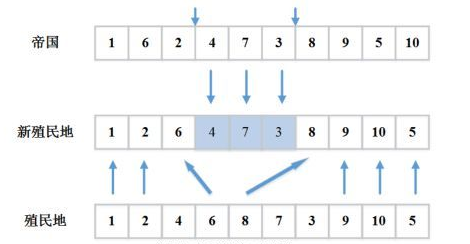
3. 殖民地革命
殖民地革命是对殖民地进行一定的移动,希望其能更靠近最优解的位置。但通常而言,对于一个社会来讲,不是说有的革命都是成功的有益的。革命也可能导致资源内耗,无法进行有效的社会变革从而降低殖民地的力量(参照苏联)。一个殖民地革命的例子如下(和GA中的变异很像对不对):
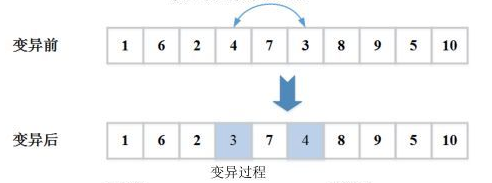
当一个殖民地国家通过同化和革命移动到一个新的位置后,殖民地的代价函数值可能比帝国主义国家小,也就是说殖民地的势力更大。此时,交换殖民地和帝国主义国家的位置,即殖民地成为该帝国的帝国主义国家,而原来的帝国主义国家则沦为殖民地。[2]
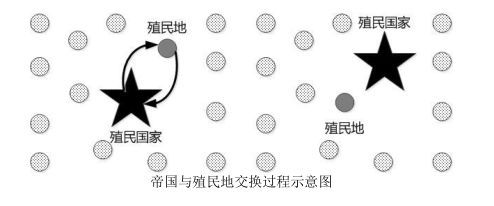
完成上述步骤后,需要对帝国的权力进行重新计算。常见的计算方式是对帝国的权力和该帝国下的所有殖民地国家的权力进行加权。当然你直接加总也应该是可以的,具体还是取决于算法如何进行设计。
4. 帝国竞争
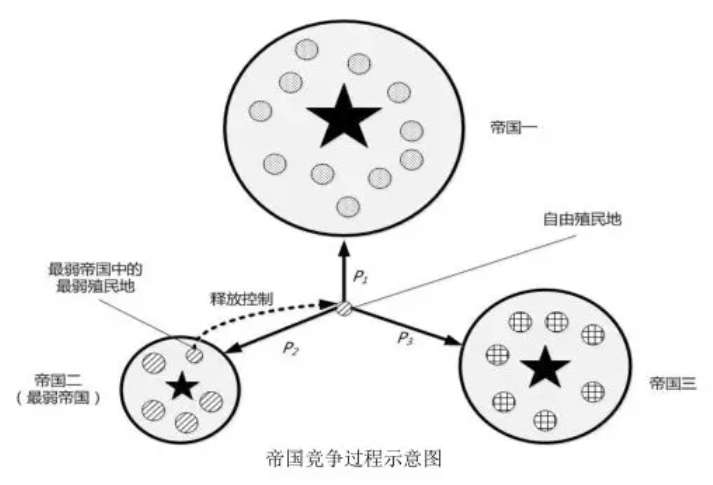
帝国竞争机制模拟的是现实社会中势力较强的帝国占有并控制势力较弱帝国的殖民地的过程。首先,需要计算帝国的总代价函数值,即势力大小。帝国主义国家对整个帝国的势力影响较大,而殖民地国家的影响非常小,因此ICA采用如下公式计算一个帝国的总代价:
其中,\(imp_n\) 是第$ n \(个帝国的帝国主义国家;\)T . C_{\cdot n}\(是第\) n $个帝国的总代价;\(0 < \xi < 1\),\(\xi\)的大小决定了殖民地国家对整个帝国势力的影响程度。选择最弱的帝国中最弱的殖民地作为帝国竞争的对象,势力越大的帝国越有可能占有该殖民地。[2]
一般的做法是将势力最弱的那个帝国中最弱的殖民地重新分配给势力最强的帝国。
5. 帝国消亡
帝国之间的竞争,使势力大的帝国通过占有其他帝国的殖民地变得越来越强大,而势力弱的帝国殖民地个数不断减少,当一个帝国丢失所有的殖民地时,帝国覆灭。随着帝国的灭亡,最终剩下一个帝国,此时算法终止。[2]
动态演示
最后可以给大家看看该算法的一个动态演示过程:

大家也可以用电脑打开
https://tomsiemek.github.io/imperialistic-competitive-algorithm-visualisation/
进行访问,可以看到该算法的详细演示过程。可以看到,随着迭代的进行,大国不断吞并效果,最终剩下的帝国数量越来越少。正所谓分久必合嘛。最终剩下的几个帝国就代表着算法搜索到的比较优秀的解了。
代码
代码从GitHub上找的,自己修改了一些地方确保能够运行,原地址:
https://github.com/robinroche/jica
欲下载本文相关的完整代码及算例,请关注公众号【程序猿声】,后台回复【ICAJAVA】不包括【】即可

main函数写在了TestICA.java里面。其中代码是求解数学优化问题的,其适应度函数计算可以找到FitnessFunction.java中的getFitnessValue进行修改,比如Sphere function、Rastrigin function和Ackley function等。其他的大家就自己慢慢研究啦。
/**
* Returns the fitness of one country
* @param individual the solution to evaluate
* @return the fitness
*/
public double getFitnessValue(double[] individual)
{
double fitness = 0;
// Sphere function
for(int i=0; i<individual.length; i++)
{
fitness = fitness + Math.pow(individual[i],2);
}
// // Rastrigin function
// for(int i=0; i<individual.length; i++)
// {
// fitness = fitness + (Math.pow(individual[i],2)-10*Math.cos(2*Math.PI*individual[i]));
// }
// fitness = 10*dimension + fitness;
// // Rosenbrock function
// for(int i=0; i<individual.length-1; i++)
// {
// fitness = fitness + 100*Math.pow((Math.pow(individual[i],2)-individual[i+1]),2) + Math.pow((individual[i]-1),2);
// }
// // Ackley function
// double a = 20;
// double b = 0.2;
// double c = 2*Math.PI;
// double s1 = 0;
// double s2 = 0;
// for(int i=0; i<individual.length; i++)
// {
// s1 = s1 + Math.pow(individual[i],2);
// s2 = s2 + Math.cos(c*individual[i]);
// }
// fitness = -a * Math.exp( -b * Math.sqrt(1/individual.length*s1)) - Math.exp(1/individual.length*s2) + a + Math.exp(1);
nbEvals++;
return fitness;
}
参考资料
[1] 基于改进帝国主义竞争算法的城市轨道交通乘客路径选择方法技术
[2] 郭婉青,叶东毅.帝国竞争算法的进化优化[J].计算机科学与探索,2014,8(4):473-482

