POJ1038 Bugs Integrated, Inc.

题目来源：http://poj.org/problem?id=1038

题目大意：

　　有一家芯片公司要在一块N*M的板子上嵌入芯片，其中1<=N<=150, 1<=M<=10,但是板子上有一些格子是坏的，不能放置芯片。芯片的面积是2*3，可以横着放也可以竖着放，但不能有重叠。如下图所示：

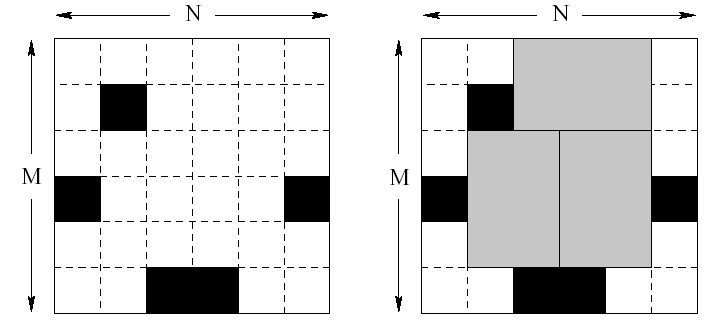
现给出N M和坏点的坐标，求最多能在板子上嵌入多少芯片。

输入：第一行测试用例数，每例第一行三个整数N、M和K，K为坏点数。接下来K行，每行一个坏点坐标（n,m），1<=n<=N,1<=m<M,0<=K<=N*M.

输出：每组输入对应一行，输出能嵌入的最大芯片数目。

---

Sample Input

2
6 6 5
1 4
4 6
2 2
3 6
6 4
6 5 4
3 3
6 1
6 2
6 4

Sample Output

3
4

---

对于没有过竞赛经验的算法弱菜来说，这题是目前为止耗费掉了最多脑细胞的题，看了题解的”状态压缩DP“，小菜表示闻所未闻，实在太高级了，汗颜。结合网上看的解题报告和”黑书“里面的各种晦涩讲解，把自己理解的一种解题思路(更准确的说是解题方法吧，因为这思路我现在看来也是神一般的)写在下面吧：

黑书上说：观察后发现，N和M的范围相去甚远，同时总数据规模较大。这就给与提示：此题很可能是需要信息加密的动态规划，即把一行看成一个整体。

[画外音：第一，对于我这种弱菜来说，显然没有感受到这种”很可能“；第二，该书整文中对行列的描述与图片与题目图片里的行列方向是不一样的，但是题目里面给出的坐标的x和y的表示是x->N, 表行号，y->M,表列号，加上网上结题报告各种行列的错乱让小菜一开始晕头转向@_@...  所以，在本文中，为了尽量避免再出现这样的问题，辛苦读者在大脑中把上面的图逆时针旋转90°，约定M表示列数，N表示行数，方向（旋转后）约定为左->右，列号1->M，下->上，行号1->N.]

好了，回到重点。由于芯片的尺寸为2*3，所以我们能否在板子上放置一块芯片，使得该芯片的左上角所在格子的坐标为[x,y]，只与[x, y]所在行和与它相邻的下面两行的占用状态（包括是否为坏点和是否被芯片占用两种情况）有关。由此启发，为每个格子设计一个状态表示方法（共三种状态，如图所示），来表示对它上一行相邻的格子能够作为芯片左上角位置的影响。

设当前格为[x,y]，

0：表示[x,y]和[x,y-1]都为空闲

1：表示[x,y]空闲, [x,y-1]被占用（为坏点或者被其它芯片占用）

2：表示[x,y]被占用，此时无论[x,y-1]是否被占用，[x,y+1]处的格子都不可能成为某块芯片的左上角，所以不用管它的占用情况了

设计好了单个格子的状态表示之后，为了进行状态压缩，把一行中表示各个格子的状态值（第i列的格子状态值称p[i]）组成的序列(看成是一个三进制串p[1]p[2]...p[M])换算成一个10进制数state，用来表示这一行的状态。一行有M格，每格有3种可能的状态，那么一行总共有3^M种状态。M的最大值为10，所以，一行最多的状态数为3^10=59049。

设计好了行的状态表示，接下来需要设计dp的状态和状态转移方程(各种状态@_@).

二维dp表中dp[i][j]表示当第i行的状态为j时，前i行放置芯片的最大数量。0<=i<=N, 0<=j<=3^M. 这样，就可以用当前行的状态推出上一行的放置情况(因为行状态j已经包含了两行格子的状态信息，所以有dp[i]足以推出dp[i+1]的信息, 这是后面使用滚动数组的基础)。

初始时把dp表的所有元素初始化为-1，表示该状态不可达或尚未开始考虑。

由一行的各列格子状态推出上一行的该列格子状态的规律是：q[i] = (p[i] == 0 ? 0 : p[i]-1); （q表示相邻上一行的格子的状态，分别试试三种情况就知道了）此时，还没有考虑上一行是否遇到坏点，所以当上一行这一列遇到了坏点，则q[i]应该变为2.

接下来是状态转移方程，考虑格子[i, y]时，有三种情况：

1. [i,y]不放芯片，转到[i,y+1];

2. [i,y]放纵向芯片，需要纵向的6个空格，所以条件为p[y] == 0 && p[y+1] == 0 && q[y] == 0 && q[y+1] == 0，更新dp[i+1][j']，j'为放了该块芯片后的i+1行状态，转到[i,y+2];

3. [i,y]放横向芯片，需要横向的6个空格，所以条件为y+2 <= M && q[y] == 0 && q[y+1] == 0 && q[y+2] == 0，更新dp[i+1][j']，j'为放了该块芯片后的i+1行状态，转到[i,y+3];

至此，dp的过程已经介绍完了(不知道讲清楚了几成=_=b)，另外的一点优化就是上面提到的由于dp表一行一行更新时不需要前面更多行的信息，所以可以使用滚动数组来压缩存储，即循环利用数组的空间。

另一个优化在于：基于”加快经常性事件“的思想，本题里3进制和10进制的转换是频繁事件，选择高效的转换方法可以大大提高程序效率，由于位数确定且较少，可以预先计算好各位的权重。

//////////////////////////////////////////////////////////////////////////
//        POJ1038 Bugs Integrated, Inc.
//        Memory: 720K        Time: 969MS
//        Language: C++        Result: Accepted
//////////////////////////////////////////////////////////////////////////

#include <iostream>

using namespace std;

int N, M, k;
int d[2][59049];
int w[12] = {0, 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, 59049};
int p[11];
int q[11];
int badSquares[151][11];
int cnt;
int o;

inline int ternary2decimal(int a[]) {
    int sum = 0;
    for (int i = 1; i <= M; ++i) {
        sum += a[i] * w[i];
    }
    return sum;
}
inline void decimal2ternary(int code, int a[]) {
    for (int i = 1; i <=M; ++i) {        
        a[i] = code % 3;
        code /= 3;
    }
}

void dfs(int p[], int q[], int y, int cntNow) {
    int qState = ternary2decimal(q);
    if (cntNow > d[1 - o][qState]) {
        d[1 - o][qState] = cntNow;
    }
    if (cntNow > cnt) {
        cnt = cntNow;
    }
    for (int t = y; t < M; ++t) {
        if (q[t] == 0 && q[t + 1] == 0 && p[t] == 0 && p[t + 1] == 0) {
            q[t] = q[t + 1] = 2;    //放置一块纵向芯片
            dfs(p, q, t + 2, cntNow + 1);    //转至右边第二块
            q[t] = q[t + 1] = 0;
        } else if (t + 2 <= M && q[t] == 0 && q[t + 1] == 0 && q[t + 2] == 0) {
            q[t] = q[t + 1] = q[t + 2] = 2;    //放置一块横向芯片
            dfs(p, q, t + 3, cntNow + 1);    //转至右边第三块
            q[t] = q[t + 1] = q[t + 2] = 0;
        }
    }
}

int main(void) {
    int cases;
    cin >> cases;
    while(cases--) {
        cin >> N >> M >> k;
        memset(d, -1, sizeof(d));
        memset(badSquares, 0, sizeof(badSquares));
        for (int i = 0; i < k; ++i) {
            int x, y;
            cin >> x >> y;
            badSquares[x][y] = 1;
        }    
        for (int i = 1; i <= M; ++i) {
            p[i] = badSquares[1][i] + 1;
            //预先处理第一行的状态，坏点为2，
            //好点为1(可以看做人工加入了全部是坏点的第0行，
            //省去了下边界处理的问题)
        }
        d[0][ternary2decimal(p)] = 0;    //前0行可放芯片数0
        o = 0;
        cnt = 0;
        for (int i = 1; i < N; ++i) {
            memset(d[1 - o], -1, sizeof(d[1 - o]));
            for (int j = 0; j < w[M + 1]; ++j) {
                if (d[o][j] == -1) {
                    continue;
                }
                decimal2ternary(j, p);
                for (int k = 1; k <= M; ++k) {
                    q[k] = p[k] == 0 ? 0 : p[k] - 1;    //推上一行的每格状态
                    if (badSquares[i + 1][k] == 1) {
                        q[k] = 2;    //遇上坏点，状态为2
                    }
                }
                dfs(p, q, 1, d[o][j]);
            }
            o = 1 - o;
        }
        printf("%d\n", cnt);
    }
    system("pause");
    return 0;
}