POJ1003 Hangover

题目来源：http://poj.org/problem?id=1003

题目大意：

　　将一叠卡片堆放在桌边。如果有一张卡片，你可以最多让卡片的一半悬于桌边外。（假设卡片总是与桌边垂直的。）当有两张卡时，你可以让上面的一张卡片有一半悬于底下的卡片之外，下面的卡片则有1/3悬于桌外。故悬于桌外的卡片长度和为1/2 + 1/3 = 5/6.当有你张卡片时，总的悬于桌外的长度和最大为1/2 + 1/3 + 1/4 + ... + 1/(n - 1).其中，最顶端的卡片外悬1/2，第二张外悬1/3，第三张外悬1/4...最底部的一张外悬1/(n+1).如下图所示：

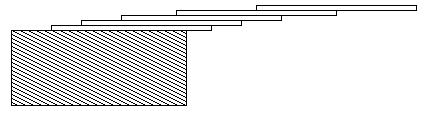
输入：有多组测试样例组成，每行包含一个正的浮点数c，最小为0.01，最大为5.20，每个c恰好为3位。以0.00作为结束标志。

输出：对于每一个测试样例，输出最少需要多少张卡片才能使总的外悬长度至少为c。使用Example Output中的格式输出。

---

 Sample Input

1.00
3.71
0.04
5.19
0.00

Sample Output

3 card(s)
61 card(s)
1 card(s)
273 card(s)

 

---

本题题干中已经把公式给出，因为数据规模小，只需从小到大逐个检验n是否可行即可。

//////////////////////////////////////////////////////////////////////////
//        POJ1003 Hangover
//        Memory: 252K        Time: 0MS
//        Language: C++        Result: Accepted
//////////////////////////////////////////////////////////////////////////

#include <iostream>

using namespace std;

int main(void) {
    while (true) {
        float length = 0.0;
        cin >> length;
        if (length == 0) {
            break;
        }
        float f = 0.5;
        int i = 1;
        while (true) {
            if (f >= length) {
                break;
            }
            else {
                i++;
                f += (1.0 / (i + 1));
            }
        }
        cout << i << " card(s)" << endl;
    }
    return 0;
}