1、什么是插入排序

它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

从第二个元素开始r[1]，那么将他左边的元素作为一个已经有序的序列，将r[1]按从小到大的顺序插入到

有序序列中的合适位置使之成为一个新的有序序列；接着将r[2]插入到左边的有序序列中，使之成为一个

新的有序序列，依次类推，直道将所有的元素都遍历完了之后，那么整个数组就是一个从小到大的有序数组了。

 

2、效果演示

        这是需要进行排序的序列

         对于第1个元素8来说，它本身就是有序的

         再来考虑第2个元素6，因为他比8小，交换一次位置

     

        再来考虑第3个元素2，因为他比8小，交换一次位置

        2又比左边的6小，交换一次位置

          再来考虑第4个元素，因为他比8小，交换一次位置

       3又比左边的6小，交换一次位置

       3比左边的2大，不需交换，前4个元素就已经排序完毕，后面的依次类推

 

2、时间复杂度

O(n^2)

 

3、算法实现(基于C++)

 1 /* 直接插入排序算法实现 */
 2 template<typename T>
 3 void insertSort(T a[], int count)
 4 {
 5     /* 找到a[i]这个元素的合适插入位置，因为第一个元素前面没有元素，无法进行比较，所以从第二个元素开始 */
 6     for (int i = 1; i < count; i++) {
 7         for (int j = i; j > 0 && a[j - 1] > a[j]; j--) {  
 8             std::swap(a[j-1], a[j]);
 9         }
10     }
11 }

 

4、直接插入算法的改进

从上面的算法实现上可知，我们的直接插入排序算法上需要进行大量的两个元素交换的动作（swap函数），而两个元素交换在实现上是需要进行3次的赋值操作，所以会给整个过程造成大量的时间浪费，所以我们将对上面在算法的实现上进行一个改进，通过改进之后可以大大的缩短直接插入排序算法的所需要的时间。

改进的思想: 其实就是通过直接的赋值操作代替大量的数组元素间的互换操作，具体的实现请看下面的演示

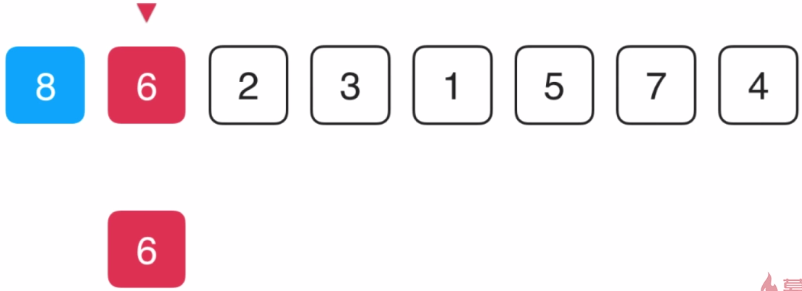 首先还是从第2个元素开始排序，这次我们先将6这个元素拷贝出来一份，然

                                      后再与左边的8进行比较，6副本比8小，将8往右移动，再将6副本指针往左移动

 

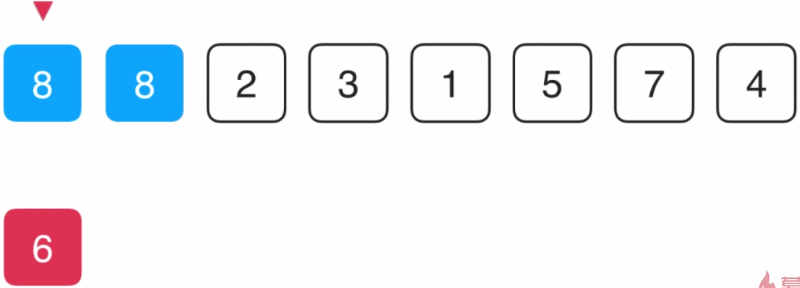  直接将6副本赋值给当前所指向的这个位置，此时前面2个元素排序完毕

 

       

 

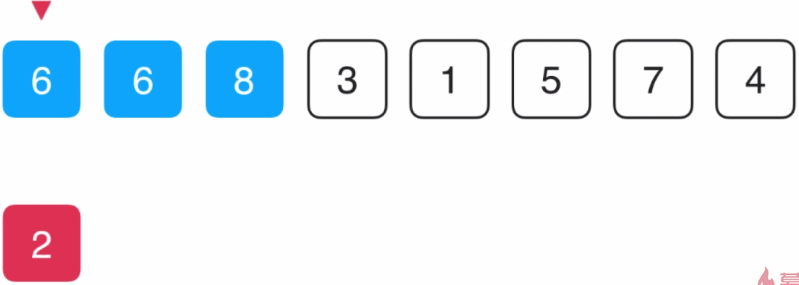
   考虑第3个元素，还是先将其复制一份，2副本比左边的8小，将8往右移动，

                                       将2副本指针往左移动

 

   2副本又比左边的6小，将6往右边移动一次，将2副本指针往左移动

 

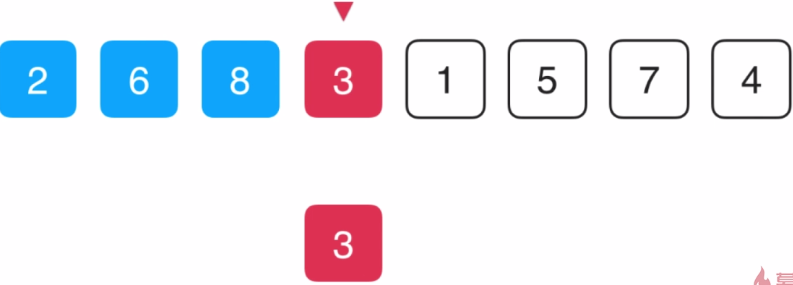
  直接将2副本赋值给当前所指向的这个位置

 

  前面3个元素排序完毕

 

  再来考虑第4个元素，首先还是先将其拷贝一份，3副本比左边的8小，直接

                                       将8往右移动，将3副本指针往左移动

 

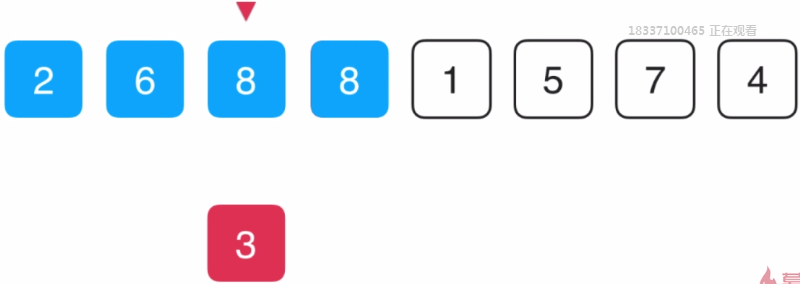  3副本又比左边的6小，将6往由移动，3副本指针往左移动

 

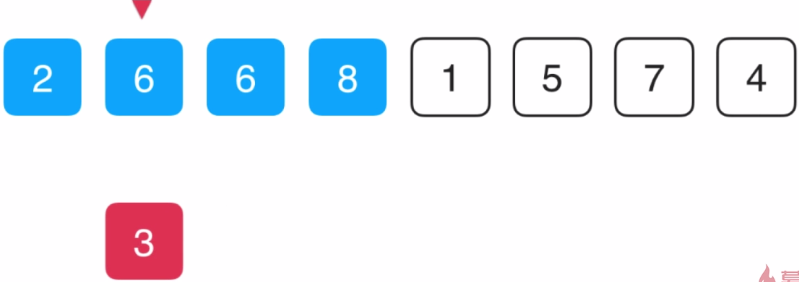  此时3副本比左边的2大，这个位置合适，将3副本赋值给当前所指向的这个位置

 

  至此前面的4个元素排序完毕，依次类推

 

由此可以知道经过上面的方法之后，减少了两个元素之间的交换操作，大大缩短了时间。

算法的实现如下:

 1 /*********************************** 直接插入排序算法实现 ********************************/
 2 template<typename T>
 3 void insertSort (T a[], int count)
 4 {
 5     /* 找到a[i]这个元素的合适插入位置，因为第一个元素前面没有元素，无法进行比较，所以从第二个元素开始 */
 6     for (int i = 1; i < count; i++) {
 7         int j;
 8         T copy = a[i];           // 将需要插入到左边有序序列的元素拷贝出来作为一个副本
 9         for (j = i; j > 0 && a[j - 1] > copy; j--) { 
10             a[j] = a[j - 1];     // 如果条件满足，直接前一个元素赋值给后面的元素
11         }
12         a[j] = copy;             //  找到该元素的合适位置之后直接赋值即可
13     }
14 }
15 /**********************************************************************************************/

我们将一系列的元素之间的交换变成了赋值操作，大大的缩短了排序所需要的时间，可以大大提高程序运行的效率。

 

5、总结

(1)插入排序的时间复杂度是O(n^2)级别

(2)插入排序的内层循环是可以提前终止的，因为只要找到了合适的位置，将元素插入到该位置后就可以终止本次循环了。

(3)如果需要进行排序的数组序列本来就是一个非常有序的状态，那么插入排序执行起来的效果将比选择排序快上很多，因为插入排序的内层循环将大大的减少时间，而选择排序内层循环每一次都会循环到底，所以在时间上将远远超过插入排序，所以当需要排序的数组序列本来就是一个非常有序的状态，那么内层的循环基本上不用做了，这样会大大提升效率。当需要进行排序的序列几乎接近于有序时，插入排序的时间复杂度将会变为n级别。