长短时记忆网络LSTM和条件随机场crf

LSTM 原理

CRF 原理

给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型。假设输出随机变量构成马尔科夫随机场(概率无向图模型)
在标注问题应用中，简化成线性链条件随机场，对数线性判别模型，学习方法通常是最大似然估计或正则化的最大似然估计。

概率无向图模型：

无向图表示的联合概率分布。

1. 定义：

成对马尔科夫性，局部马尔科夫性，全局马尔科夫性，

上述三个性质定义等价，主要阐述，三个集合，A, B, C，其中集合A和B表示在无向图G中被结点集合C分开的任意结点集合

给定随机变量组Yc的条件下，随机变量组Ya和Yb是条件独立的。

满足三条性质就是的联合概率分布P(Y)就是联合概率无向图模型，如何求这个联合概率的分布，写成若干子联合概率乘积的形式。还好概率无向图模型能因子分解

2. 因子分解

团：任意两个节点均有边连接的结点子集。

最大团：不能再加进任何一个新的结点使其成为更大的团。

因子分解：表示将概率无向图上的联合概率分布表示为其最大团上的随机变量的函数的乘积形式

P(Y)可以写成图中所有最大团C上的函数Ψc(Yc)的乘积形式，Z是规范化因子

 

 

 

 

 

势函数要求是严格正的，通常是指数函数

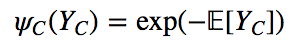
3. 条件随机场的定义：输入序列来预测输出序列的判别式模型

P(Y|X) X是需要标注的观测序列，Y是标记序列。利用训练集通过极大似然估计得到条件概率模型。在测试过程，对于给定的观测序列，模型需要求出条件概率最大的输出序列。

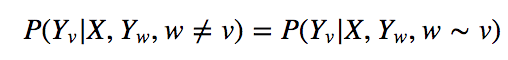
对任意结点v都成立，则P(Y|X)为条件随机场，就是做了一个假设简化了计算，只考虑相连，忽略外围其他边。

中 w≠v表示 w 是除 v 以外的所有节点，w∼v表示 w 是与 v 相连接的所有节点。

线性链条件随机场的定义：

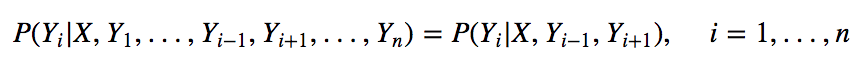
其中当 i 取 1 或 n 时只考虑单边。

4. 线性链条件随机场的数学表达式

线性链条件随机场的参数化形式：特征函数及例子

Z(x) 作为规范化因子，是对 y 的所有可能取值求和。

tk特征函数定义在边上，称为转移特征，依赖当前和前一位置，sl特征函数定义在结点上，称为状态特征，依赖当前位置。两者取值0或1，当特征条件满足为1，不满足为0，条件随机场完全有特征函数tk，sl和对应权重确定。

tk和sl相当于给定的特征模板，给定y可以计算出该标记序列的条件概率。

以序列标注为例：

 

序列标注 vs 分类

序列标注不是简单的分类，这两类问题存在非常大的区别

lstm处理特征fc到类别数后直接softmax效果没有crf好，因为为每一个待标注的位置都当作一个样本然后进行分类，这样单点的分类，将会有很大的信息损失，因为一个序列的不同位置之间存在联系，应该对这个相关性建模。

条件随机场的简化形式：

这种双重求和就表明了对于同一个特征(k)，在各个位置(i)上都有定义。将某一特征模板在所有位置上求和的做法相当于在将局部特征转化为全局特征函数，从而可以写成内积形式。

矩阵形式：

这种形式依托于线性链条件随机场对应的图模型仅在两个相邻节点之间存在边。在状态序列的两侧添加两个新的状态 y0=start 、yn+1=stop。

未完待续

 

 

线性链条件随机场的解码问题

解码问题即预测问题，给定条件随机场 P(Y|X) 和观测序列 x ，求最有可能的状态序列 y^* 。与 HMM 类似，使用维特比算法求解。

线性链条件随机场的学习问题

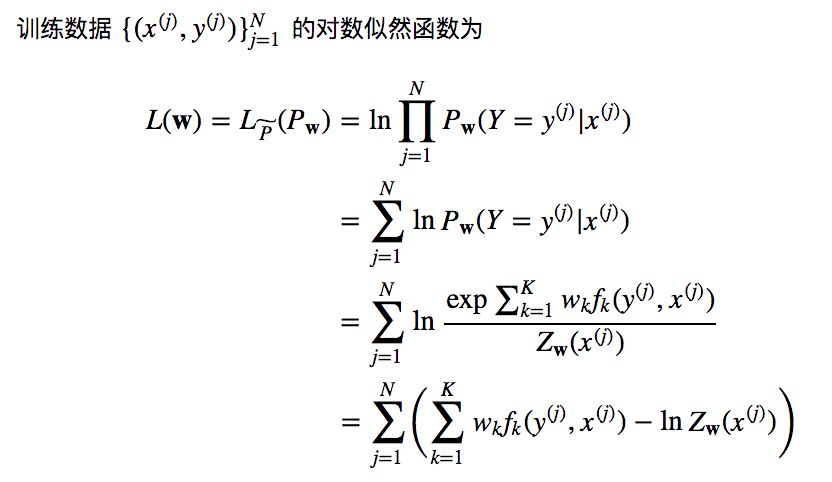
对权重w求导