POJ 1930 Dead Fraction (循环小数-GCD)
题意:给你一个循环小数,化成分数,要求分数的分母最小。
思路:暴力搜一遍循环节
把循环小数化分数步骤:
纯循环小数化分数
纯循环小数的小数部分可以化成分数,这个分数的分子是一个循环节表示的数,分母各位上的数都是9,9的个数与循环节的位数相同。能约分的要约分。
混循环小数化分数
这个分数的分子是第二个循环节以前的小数部分组成的数与小数部分中不循环部分组成的数的差。分母的头几位数是9,末几位是0。9的个数与循环节中的位数相同,0的个数与不循环部分的位数相同。
例:
回到问题
将题目小数部分提取出来,从后往前搜索,后面部分作为循环部分,前面部分作为不循环部分。按上述方法求出分子分母,记录最小分母即可。
#include <cstdio>
#include <iostream>
#include <string>
#include <cmath>
using namespace std;
typedef long long LL;
LL Gcd(LL a, LL b) {
LL t;
while (b) {
t = a % b;
a = b;
b = t;
}
return a;
}
LL _stoll(string s) { // c++11 std::stoll
LL v = 0;
for (int i = 0; i < s.length(); ++i) {
v = v * 10 + s[i] - '0';
}
return v;
}
int main() {
string s, sa, sb;
LL la, lb;
LL num, den, g;
LL ansd, ansn;
while (cin >> s && s.length() > 1) {
s = s.substr(2, s.length() - 5);
int n = s.length();
ansd = 0;
for (int i = 0; i < n; ++i) {
int j = n - i;
sa = s.substr(0, i);// 非循环部分
sb = s.substr(i); // 循环节部分
la = i ? _stoll(sa) : 0;
lb = _stoll(sb);
num = la * (LL)pow(10, j) + lb - la; //小数部分-非循环部分
den = ((LL)pow(10, j) - 1) * (LL)pow(10, i);//999000
g = Gcd(num, den);
num /= g;
den /= g;
if (!ansd || den < ansd) {
ansd = den;
ansn = num;
}
}
printf("%lld/%lld\n", ansn, ansd);
}
return 0;
}

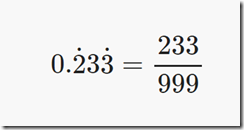


 浙公网安备 33010602011771号
浙公网安备 33010602011771号