从算法到算命—八大排序算法之快速排序篇

从算法到算命—八大排序算法之快速排序篇

核心思想

枢轴选定快排开，左右分割逐层排。

小者归左大归右，交换位置继续摆。

高低元素如相换，移动指针向枢轴。

高低指针如相遇，选中指针所落入

递归分治排子表，直至左右仅一头。

算法描述

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

• 从数列中挑出一个元素，称为 “基准”（pivot）或者叫 “枢轴” ；
• 重新排序数列，所有元素比枢轴值小的摆放在枢轴的左边，所有元素比枢轴值大的摆在枢轴的右边（相同的数可以到任一边）。在这个分区退出之后，该枢轴就处于数列的中间位置。这个称为分区（partition）操作；
• 递归地（recursive）把小于枢轴值元素的子数列和大于枢轴值元素的子数列排序。

动图演示

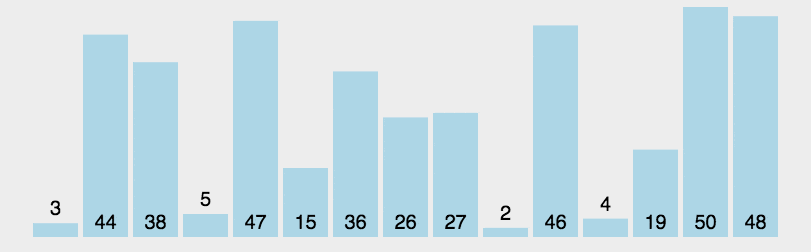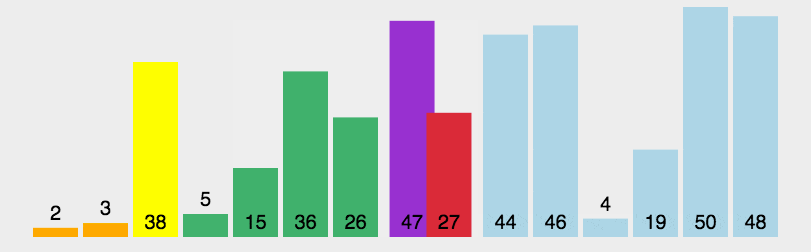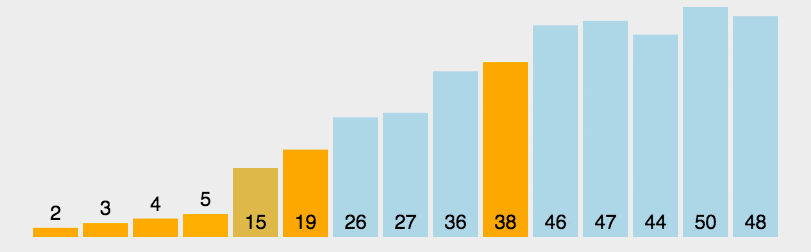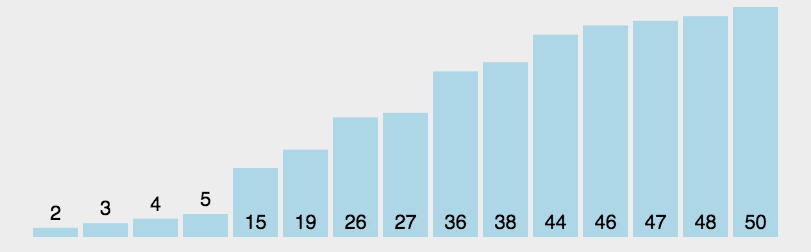
排序过程

看完以上的介绍，你是不是仍然不知道在说些什么？

没事，不要怕，咱们就是为了把它啃透才来的嘛，咱们先来看一看一开篇的打油诗。

这里面提到了一个概念叫枢轴，虽然在描述中已经介绍了枢轴的概念，但是比较抽象，不好理解，那么在这里我再对概念进行一个增强解释：

”轴“ 是干什么的呢，我们想一个概念叫做 “对称轴” ，它是不是将一个图形也好，数列也好，将其分为了两半。所以说轴嘛，就是用来区分的，把一个数列分为左边一堆，右边一堆。

那么我们的这个轴，小者归左大归右，说的就是轴的左边，放的都是比轴小的数，右边放的都是比轴大的数。

在快速排序中，我们规定，将数组的第一个元素选定为枢轴！

同样的，我们先给一个初始的数组：

在这个数组中，第一个 49 就是枢轴，以及第一个元素和最后一个元素分别为高低指针（low、high）

我们可以这样想，当枢轴确定以后，这个枢轴逻辑上就已经不在这个数列里面了，把它拿出去，那么这时候，该枢轴存放元素的位置就形成了一个空位，如果比较的元素比枢轴小，就放到这个位置上，然后移动的元素又产生了一个空位，就是这么一个反复的过程，直到最后高低指针指向同一个元素空位，那么就将枢轴元素放到这个位置上，然后继续递归。话不多说，让我们看看是怎样一个排序的过程：

首先把枢轴和高低指针标记出来，初始的数组就变成了下图所示：

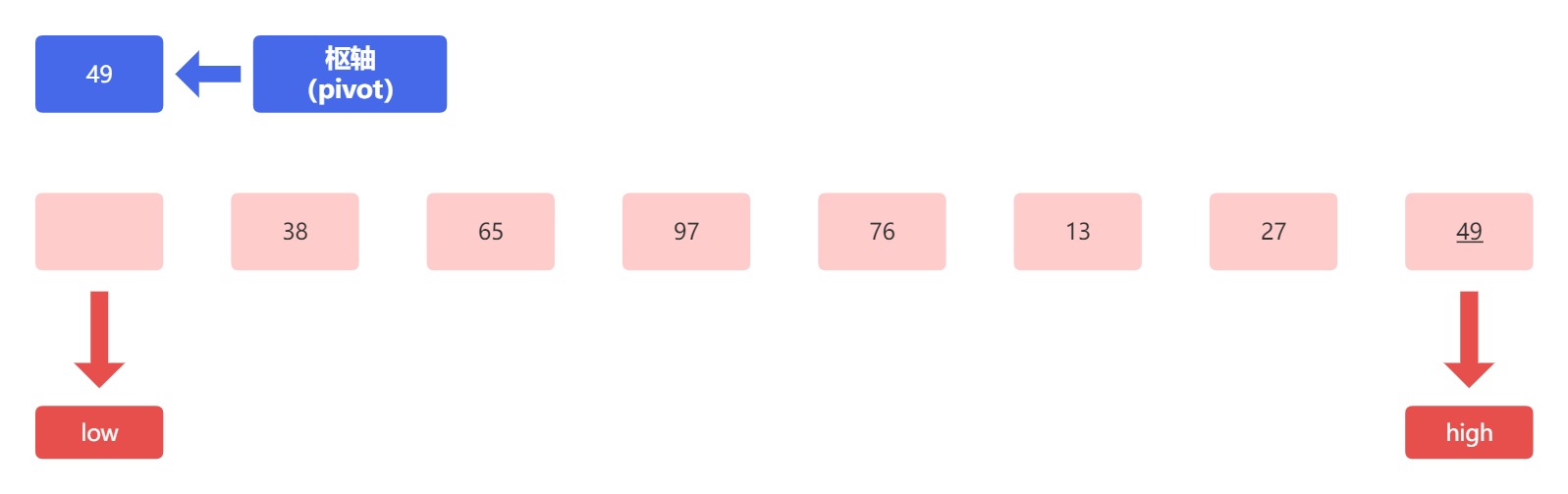
首先，枢轴元素 49 和高位指针（high）指向的元素 49 相比，这两个元素相等，所以我们不做交换，高位指针向枢轴方向移动，执行“--”操作，结果如下图：

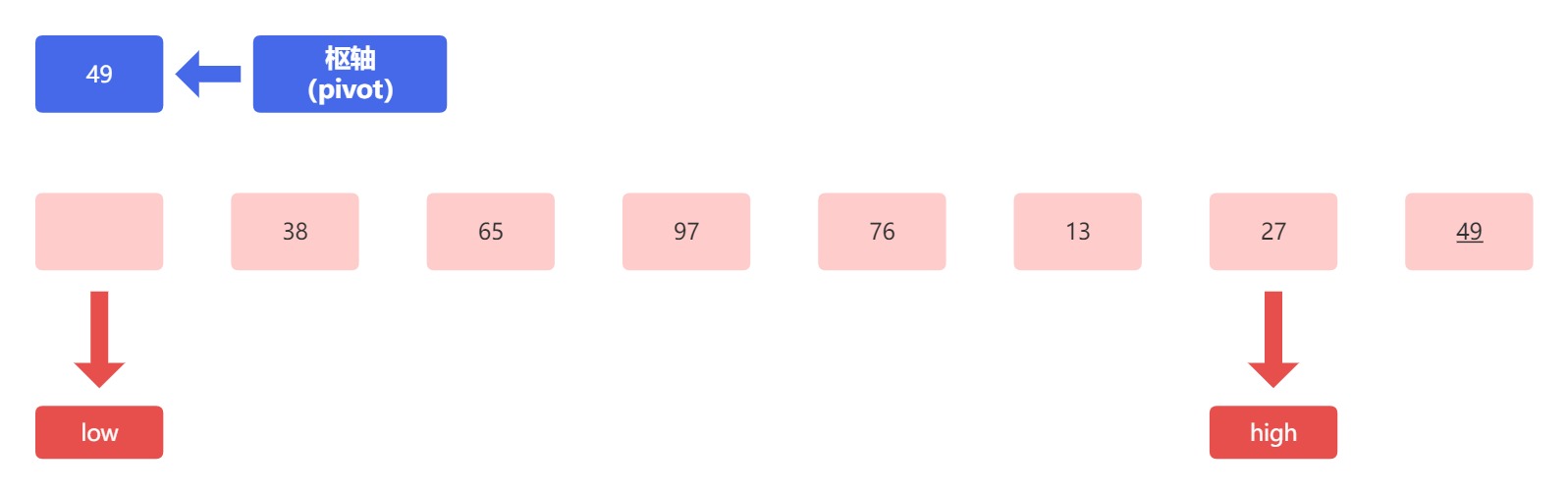
继续比较，枢轴元素 49 与高位指针指向的元素 27 进行比较，这时候 27 小于枢轴元素，小者归左大归右，比枢轴小的数往左放， 我们把 27 放到空位上，这时候，27 原本上的位置就变成了一个 ”空位“ 。

高低元素如相换，移动指针向枢轴，这句说的是，如果发生了元素交换位置，那么此时一定存在一个空位。而非空位上的指针要进行移动的操作。对于数组来说，枢轴就像一个中轴一样，小的放左边，大的放右边，移动指针向枢轴就是指针要向着枢轴的方向移动，即低位指针向右移动，高位指针向左移动。

因此，此次比较后，我们的数组应该是这样的：

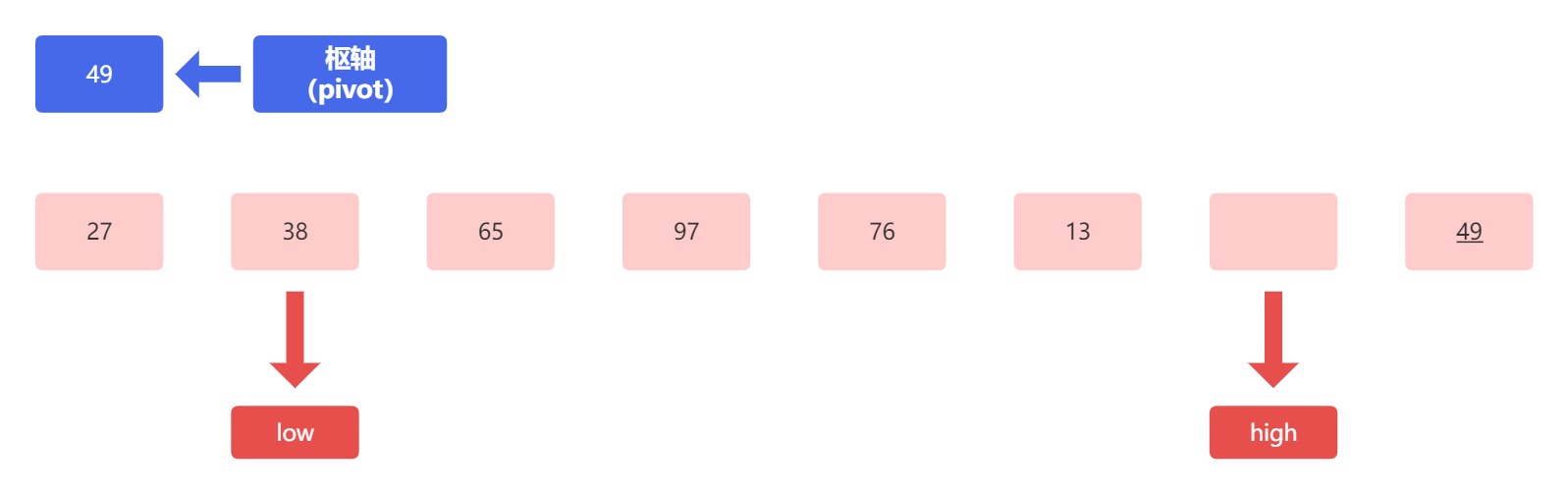
接下来，比较低位指针上的 38 和枢轴元素 49 进行比较，因为 38 小于 49 ，满足小者归左，所以不用移动，指针继续后移：

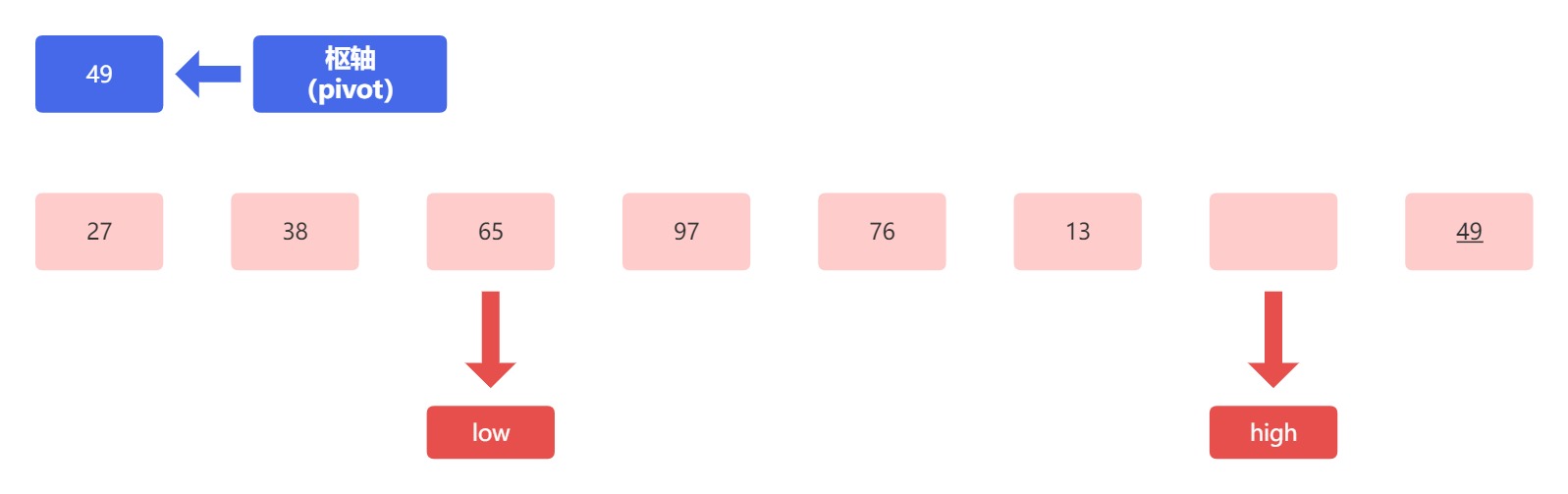
接下来对比低位指针上的 65 和枢轴元素 49 ，因为 65 大于 49 ，所以将 65 放到高位指针的空位上，此时低位指针指向的位置就形成了空位，高位指针前移：

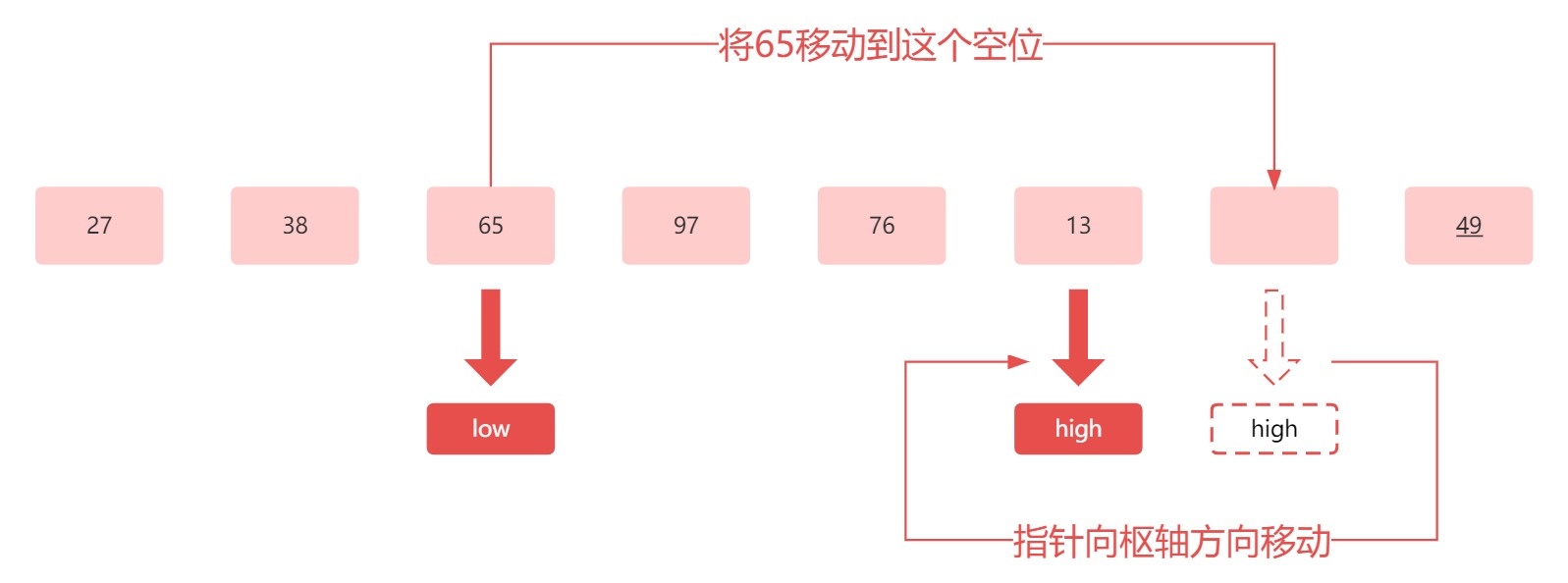
所以我们得到的结果应为：

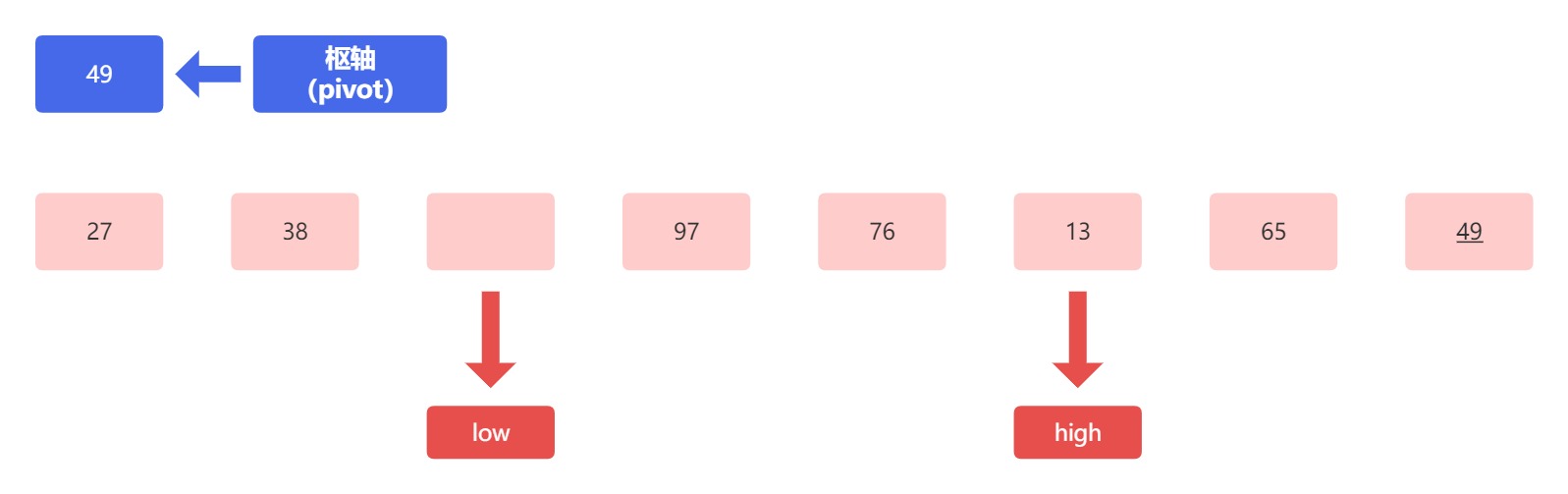
此时，因为低位指针指向的是一个空位，所以我们比较高位指针上的元素 13 和 枢轴元素 49 。此时我们发现 13 小于 49 ，所以我们要对其进行交换和移动指针的操作：

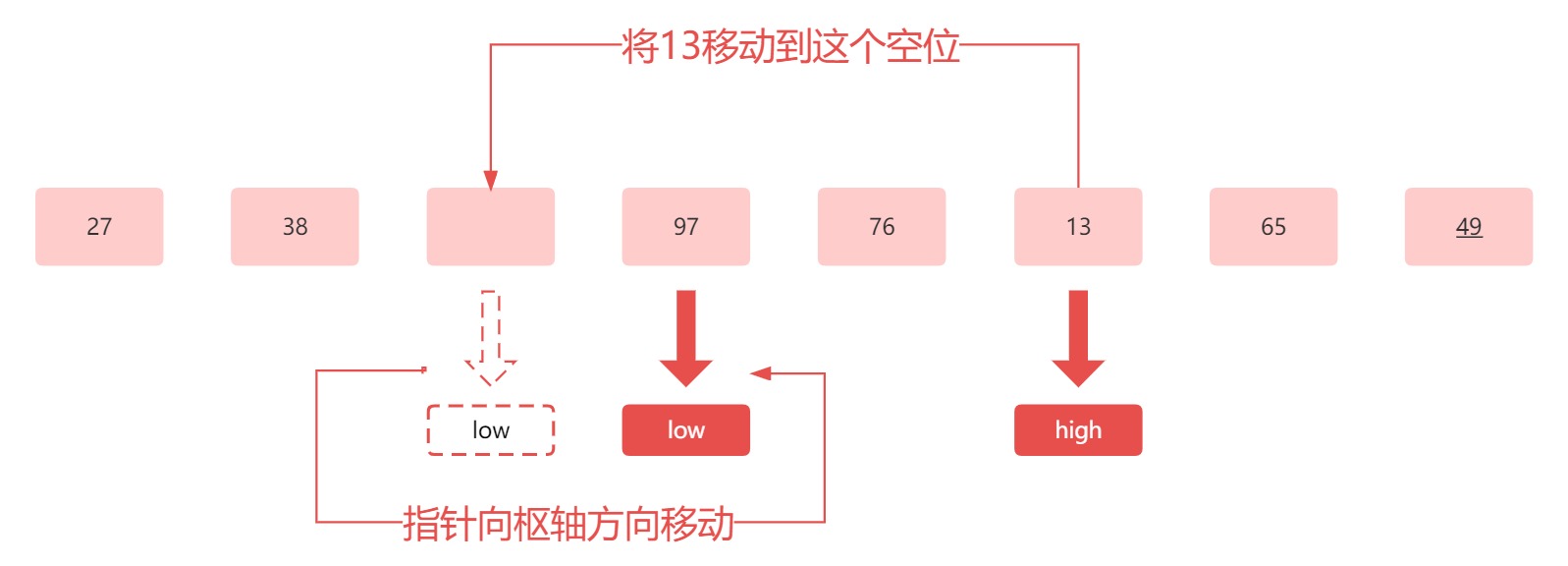
得到的结果应该为：

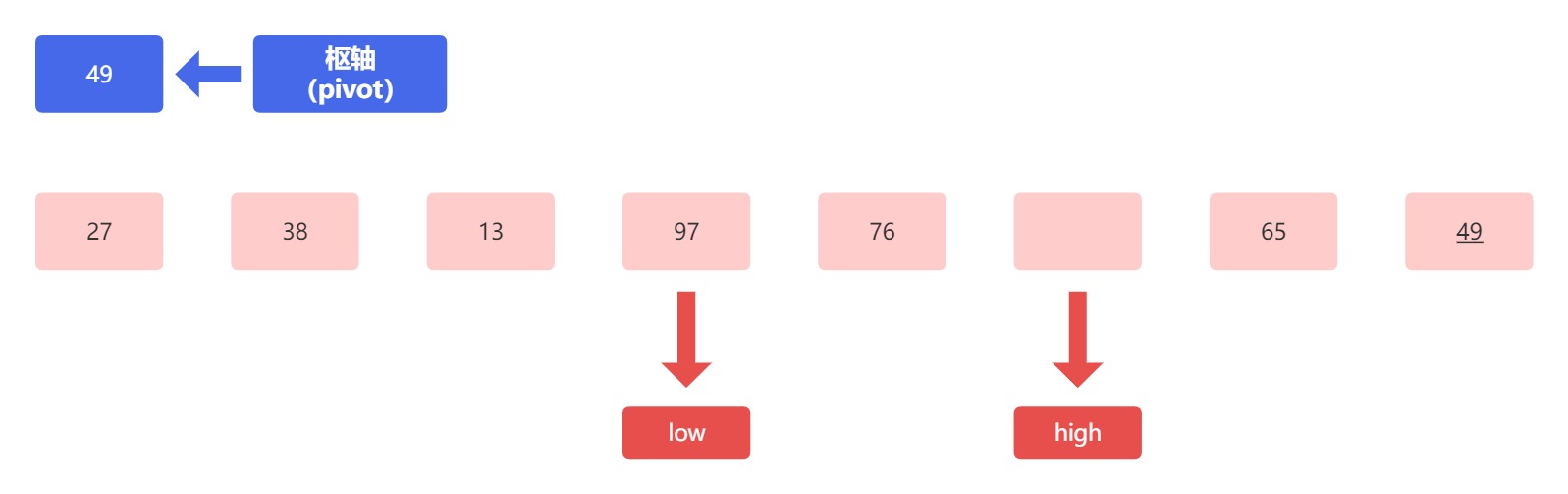
接下来对比低位指针所指向的元素 97 和枢轴元素 49 ,低位指针指向的元素大于枢轴元素，所以将 97 放到高位所指向的空位上：

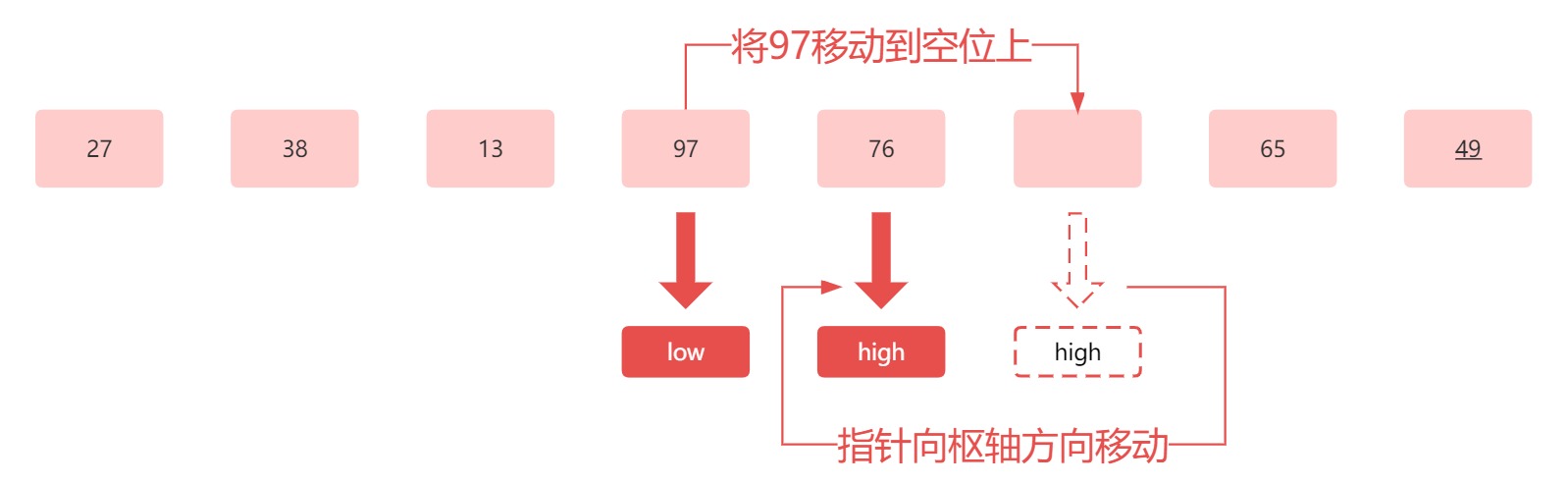
得到的结果应为：

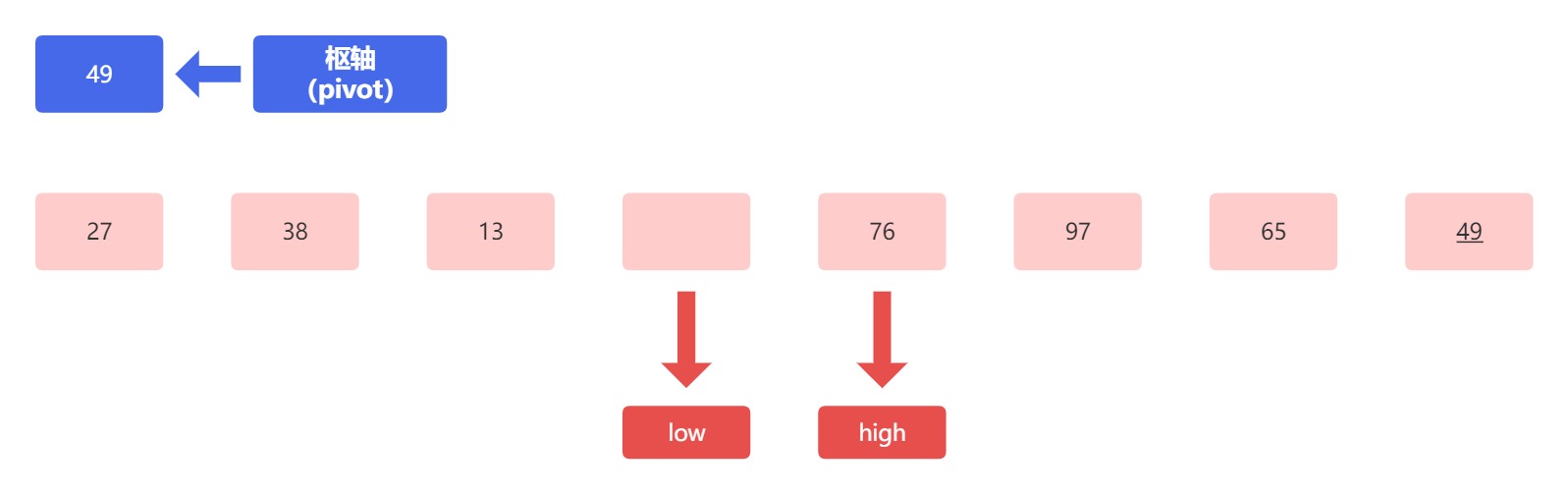
接下来比较高位指针指向的元素 76 和枢轴元素 49 因为 76 大于 49 ，所以不用进行交换，只需要移动高位指针位置即可，此时，高低位指针指向同一个位置，根据高低指针如相遇，选中指针所落入，将枢轴元素放到空位上，此时第一趟排序结束。

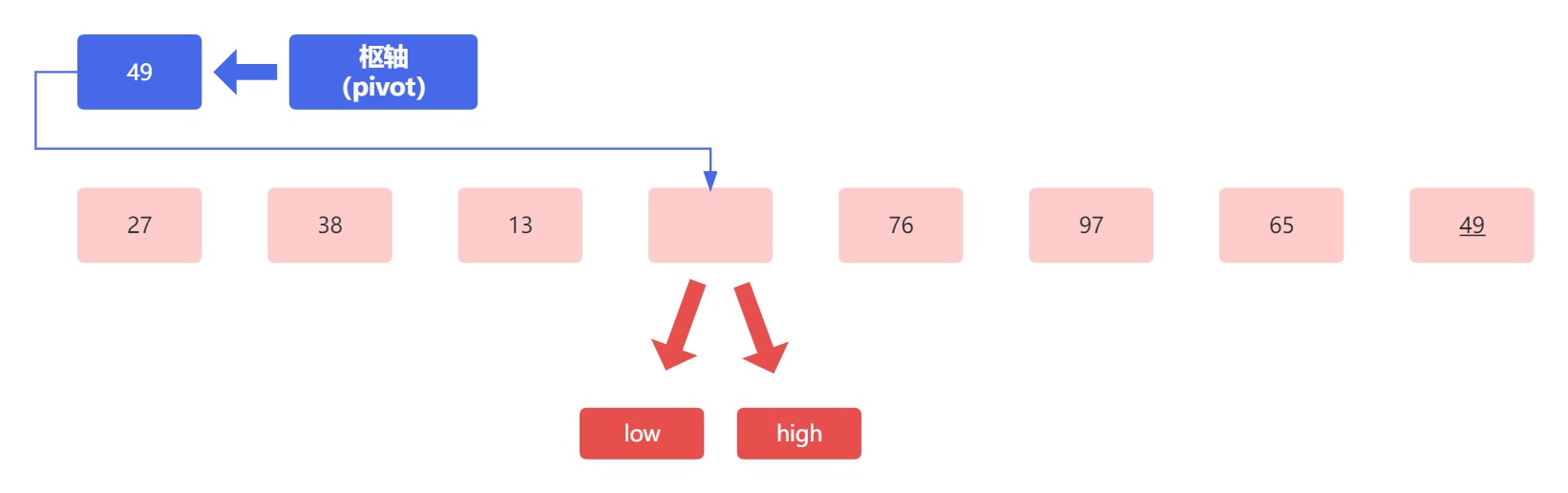
落入枢轴后的结果为：

此时我们可以看到，经过第一趟排序后，枢轴元素（蓝色方块内）左边元素的值都小于枢轴元素，而右边的元素的值都大于枢轴元素。然后就是打油诗中的最后一句递归分治排子表，直至左右仅一头。

此时你可能会有疑问了，哪里来的子表？左右仅一头又是什么意思？不要着急，我们继续来看。

我们之前说过，轴就是用来区分的，此时通过枢轴已经将数组分为了两个部分，然后将这两个部分作为两个子数组，我们先称为左侧子数组和右侧子数组。

左侧子数组 [27,38,13]

右侧子数组 [76,97,65,49]

得到了这两个子数组后，我们将递归地对左侧子数组和右侧子数组进行排序。

注意，快速排序体现的是分治的思想，所以左右子数组的排序是同时进行的，这样可以提高排序的效率。

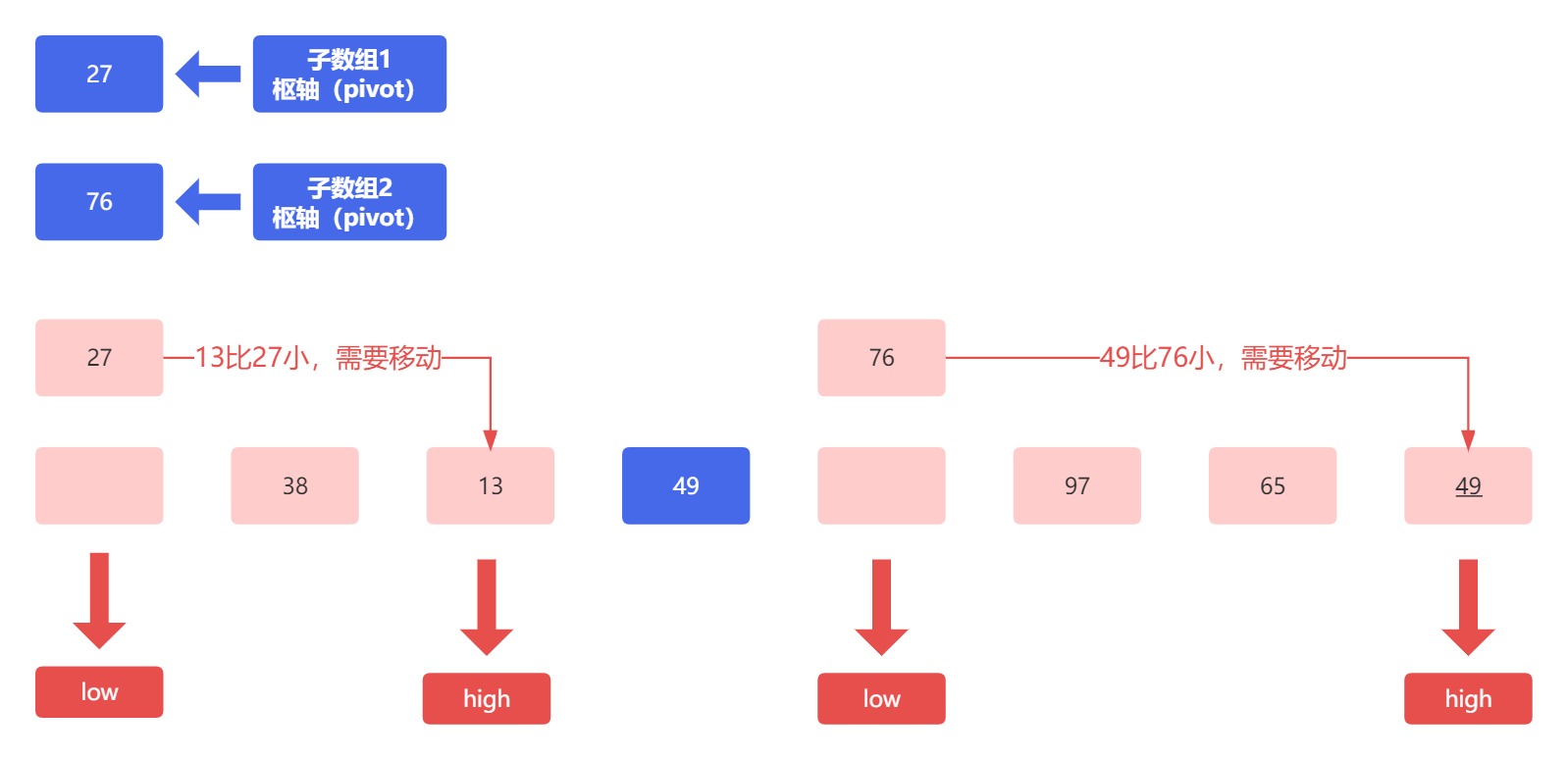
当元素位置发生变化时，我们还需要移动指针，得到的结果如下：

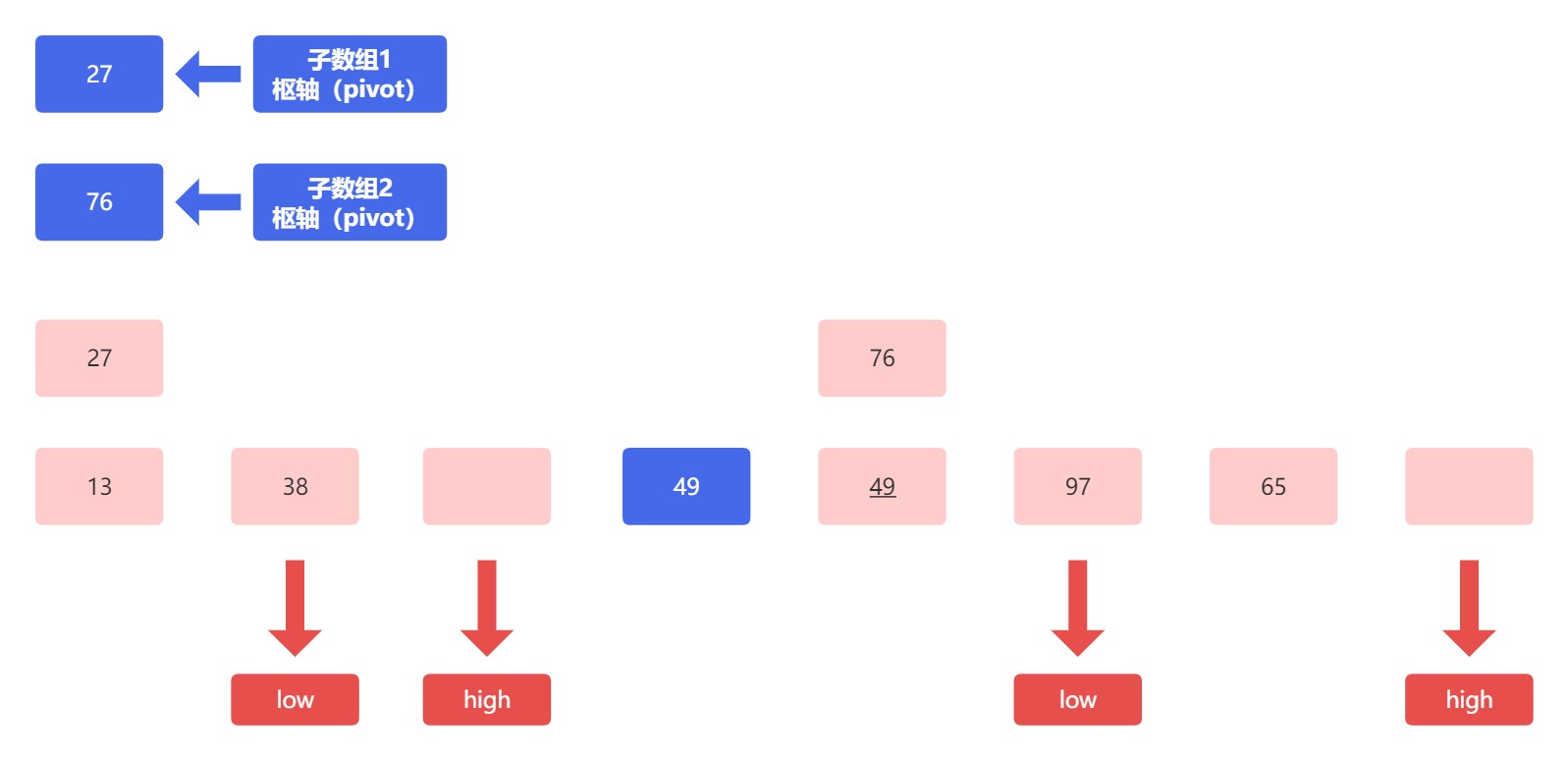
接下来，左侧子数组需要比较低位指针指向的元素 38 和枢轴 27 ;右侧子数组需要比较的是低位指针指向的元素 97 和 枢轴 76 :

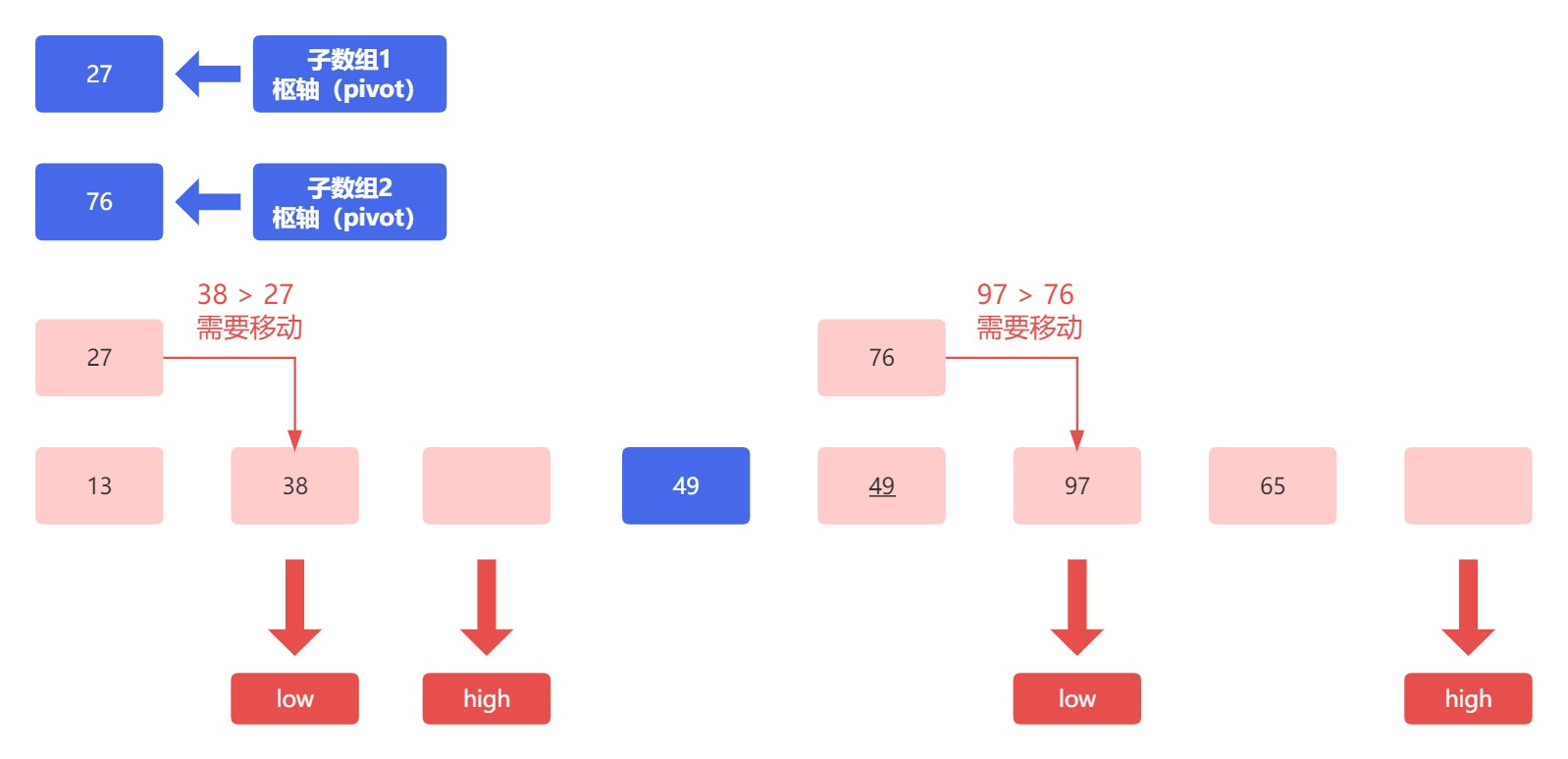
左侧子数组和右侧子数组中低位指针元素移动，产生空位，高位指针向前移动。此时左侧子数组高低位指针指向同一个空位，所以将枢轴元素放进来。此时我们发现，左侧子数组枢轴元素前面仅剩一个元素，满足直至左右仅一头中，左侧只剩一头，所以左侧子数组排序完毕，结果为：

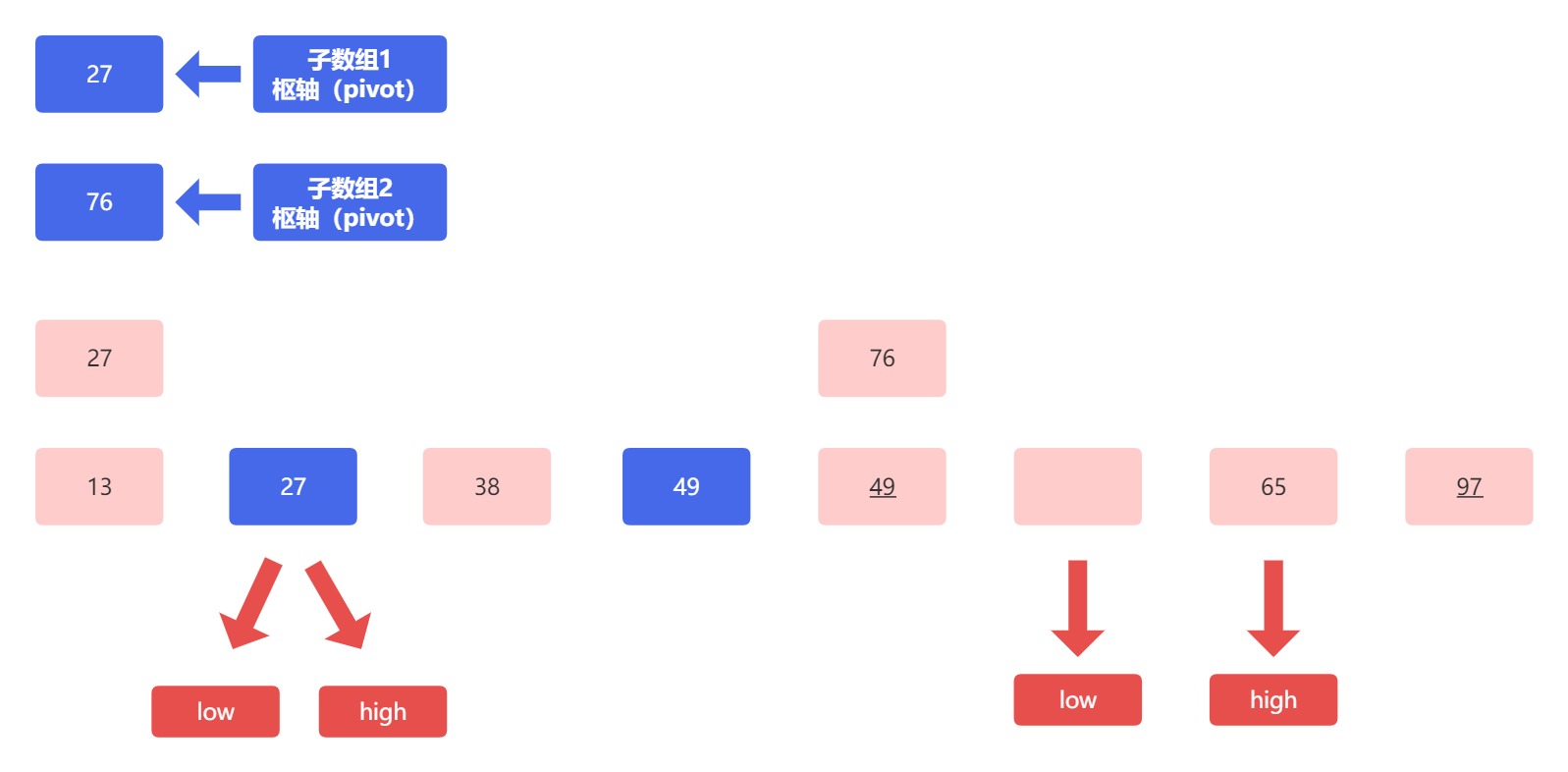
继续排序右侧子数组，需要比较的元素是高位指针指向的元素 65 以及枢轴元素 76 ,因为 65 小于 76 ，所以要进行交换：

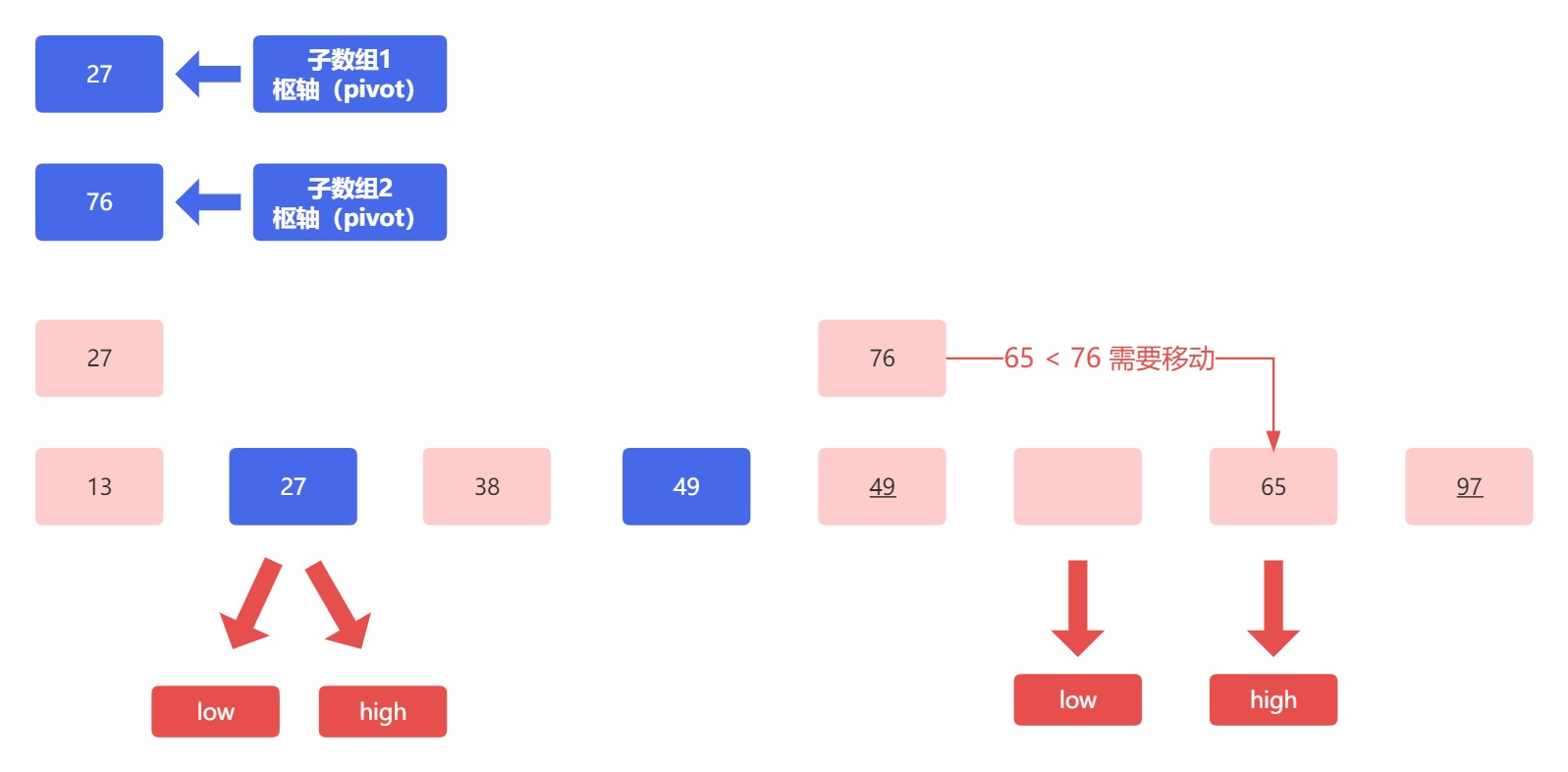
将元素移动后，需要进行指针移动的操作，此时我们发现，如果将低位指针向后移动一位之后，高低位指针将同时指向同一个空位，我们就可以把枢轴元素放进来了，此时也满足了枢轴右侧只有一个元素，符合直至左右仅一头，所以至此，右侧子数组也排序完毕，结果为：

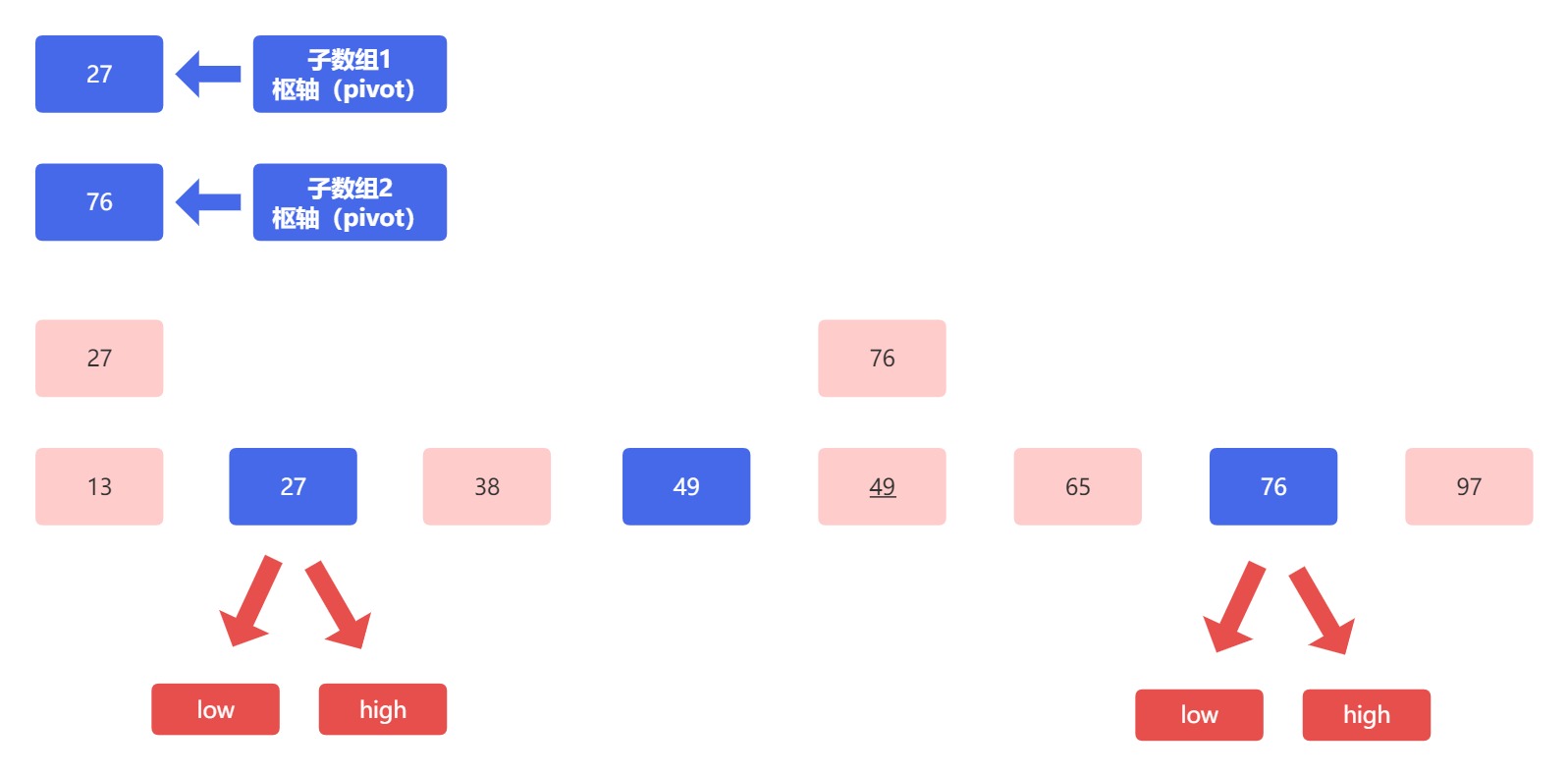
左右子数组都排序完毕，对其合并，得到了一个排序完成的数组，至此快速排序过程结束。

蓝色方块代表的是枢轴元素

代码示例（Java）

public class QuickSort {
    public static void main(String[] args) {
        int[] arr = {49,38,65,97,76,13,27,49};
        quickSort(arr, 0, arr.length - 1);

        System.out.println("排序结果：");
        for (int num : arr) {
            System.out.print(num + " ");
        }
    }

    // 快速排序算法入口
    public static void quickSort(int[] arr, int low, int high) {
        if (low < high) {
            // 对数组进行划分，并获取划分点的索引
            int pivotIndex = partition(arr, low, high);

            // 递归地对划分点左侧和右侧的子数组进行快速排序
            quickSort(arr, low, pivotIndex - 1);
            quickSort(arr, pivotIndex + 1, high);
        }
    }

    // 对数组进行划分操作
    public static int partition(int[] arr, int low, int high) {
        int pivot = arr[low]; // 选择第一个元素作为枢轴
        int left = low + 1; // 左指针从枢轴元素的下一个位置开始
        int right = high; // 右指针从数组末尾开始

        while (left <= right) {
            // 从左侧找到第一个大于枢轴的元素
            while (left <= right && arr[left] <= pivot) {
                left++;
            }

            // 从右侧找到第一个小于枢轴的元素
            while (left <= right && arr[right] > pivot) {
                right--;
            }

            if (left < right) {
                // 交换左右指针所指向的元素
                swap(arr, left, right);
            }
        }

        // 将枢轴元素放到正确的位置上
        swap(arr, low, right);

        // 返回划分点的索引
        return right;
    }

    // 交换数组中两个元素的方法
    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

这里不能使用异或（^）运算来实现交换元素的效果，因为可能出现交换的两个元素是同一个变量的情况，从而导致排序结果中会出现0的情况

快速排序特性总结

1. 分治策略：快速排序采用分治策略，将原始数组分割成较小的子数组，然后分别对子数组进行排序。通过递归地处理子问题，最终将整个数组排序。
2. 原地排序：快速排序是一种原地排序算法，不需要额外的辅助空间。在排序过程中，只需要在原始数组上进行元素交换和分区操作，不需要额外的数组来存储临时数据。
3. 不稳定性：快速排序是一种不稳定的排序算法。在分区操作中，相等元素的相对顺序可能会发生改变。如果需要保持相等元素的相对顺序，可以使用稳定的排序算法。
4. 平均时间复杂度：快速排序的平均时间复杂度为O(NlogN)，其中n是待排序数组的长度。这使得快速排序在大多数情况下具有较好的性能。
5. 最坏时间复杂度：在最坏情况下，快速排序的时间复杂度为O(n²)，即当数组已经有序或近乎有序时。为了避免最坏情况的发生，通常采用随机选择基准元素的方式。
6. 适用性：快速排序适用于各种类型的数组，包括整数、浮点数和字符串等。它具有广泛的应用，并且在实践中被广泛使用。
7. 高效性：由于快速排序采用了分治的思想，并且通过选择基准元素进行分区，使得每次递归调用可以大幅度缩小问题的规模。这使得快速排序具有较高的效率。
8. 需要额外空间：虽然快速排序是原地排序算法，但在递归调用过程中，栈空间会被使用来保存递归调用的上下文。对于大规模的数据集，可能需要较大的栈空间，因此需要考虑栈溢出的情况。