从算法到算命—八大排序算法之冒泡排序篇

从算法到算命—八大排序算法之冒泡排序篇

核心思想

两两交换，更大（小）的往后（前）放

算法描述

• 比较相邻的元素。如果第一个比第二个大（小），就交换它们两个；
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大（小）的数；
• 针对所有的元素重复以上的步骤，除了最后一个；
• 重复步骤1~3，直到排序完成。

动图演示

以升序为例：

排序过程

首先，我们先来构建一个初始无序的数组，数组内元素与之前的的一致。

那么，我们说冒泡排序是两个元素相互比较交换，我们要实现的是一个升序的排序过程，所以更大的元素应该往后放。我们来看看第一遍的过程：

首先 49 和 38 进行比较，因为49 大于 38 ，所以我们将两个元素交换位置，此时变成：

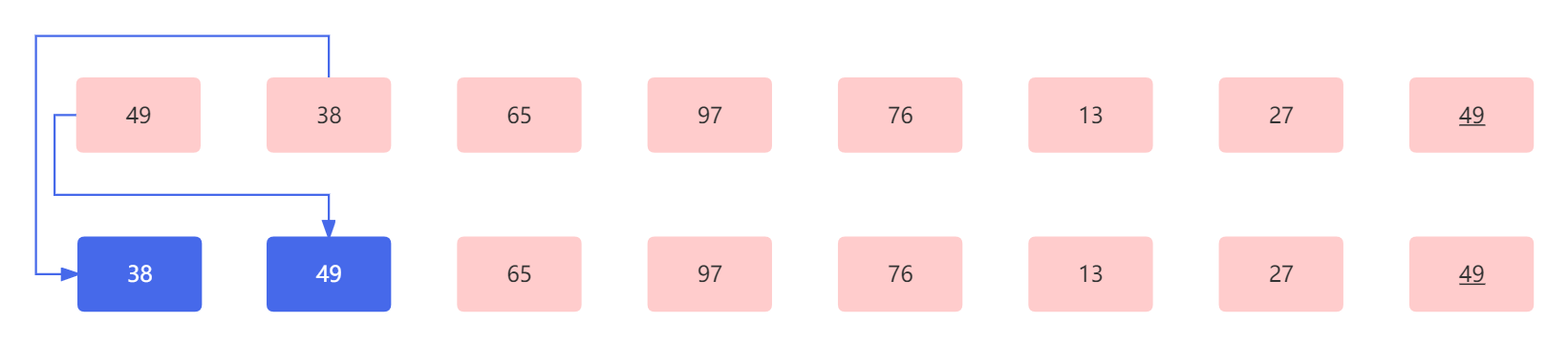
此时我们看下一对需要比较的元素，分别是 49 和 65 ，因为49 小于 65 ，所以这两个元素我们不需要交换彼此的位置，此时应为：

下一对元素 65 和 97 相比，因为65 小于 97 ，同理我们不需要交换彼此的位置，此时应为：

下一对元素 97 和 76 相比，因为 97 大于 76 ，所以两个元素需要交换彼此的位置，此时应为：

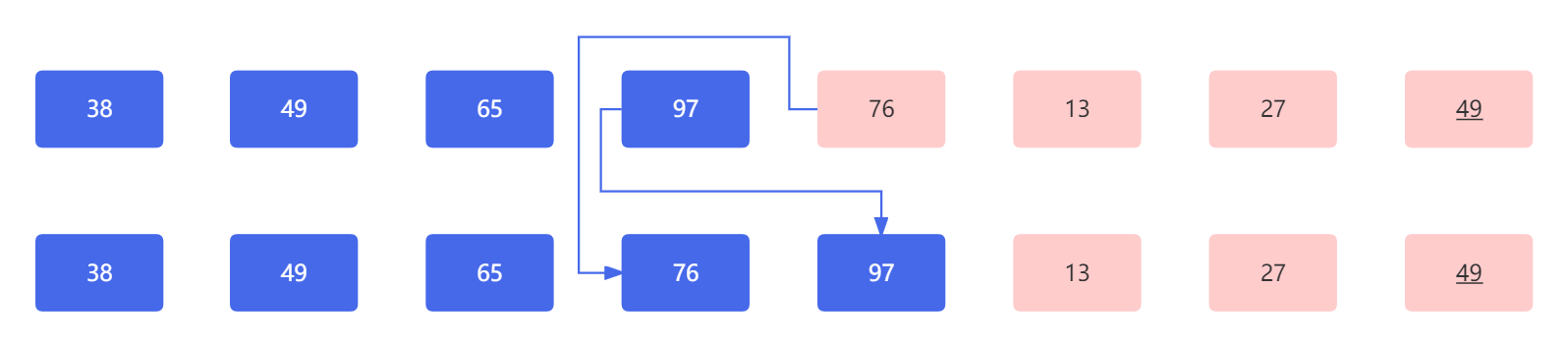
下一对元素 97 和 13 相比，因为 97 大于 13 ，所以两个元素需要交换彼此的位置，此时应为：

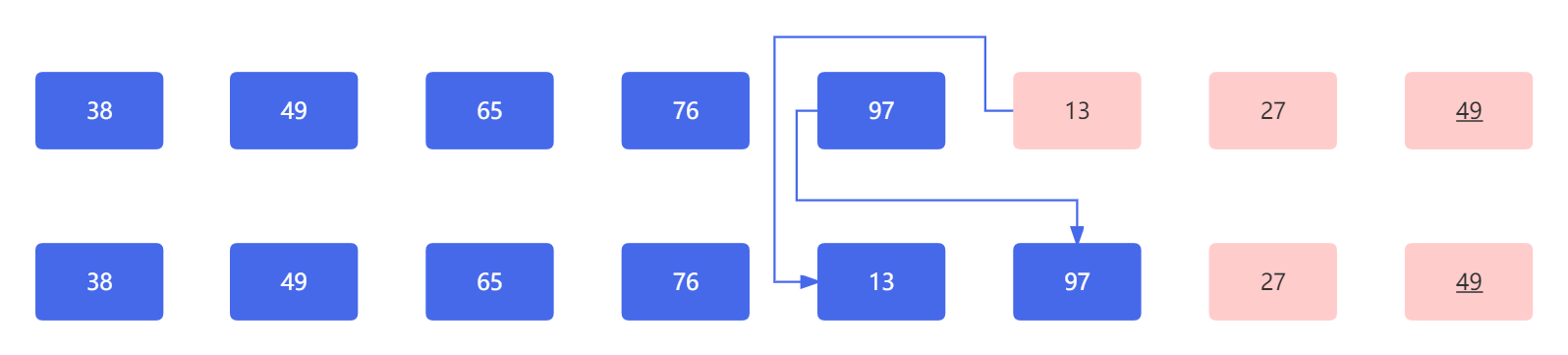
下一对元素 97 和 27 相比，因为 97 大于 27 ，所以两个元素需要交换彼此的位置，此时应为：

最后一对元素 97 和 49 相比，因为 97 大于 49 ，所以两个元素需要交换彼此的位置，此时应为：

那么至此，第一趟循环执行完毕了，我们可以看到，最大的元素 97 就像吐泡泡一样，一点一点冒到了最后一个位置。接下来，就是一个不断重复的过程：

在第二趟中，我们先看， 38 和 49 对比，顺序不用改变， 49 和 65 对比，顺序不用改变。

65 和 76 对比，顺序不用改变， 76 和 13 对比，顺序需要改变：

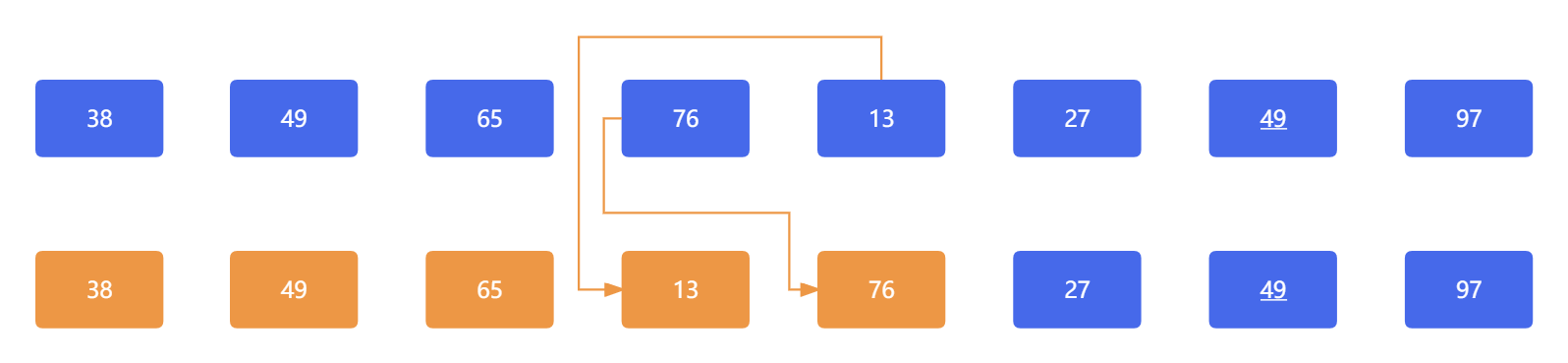
下一对元素 76 和 27 相比，因为 76 大于 27 ，所以两个元素需要交换彼此的位置，此时应为：

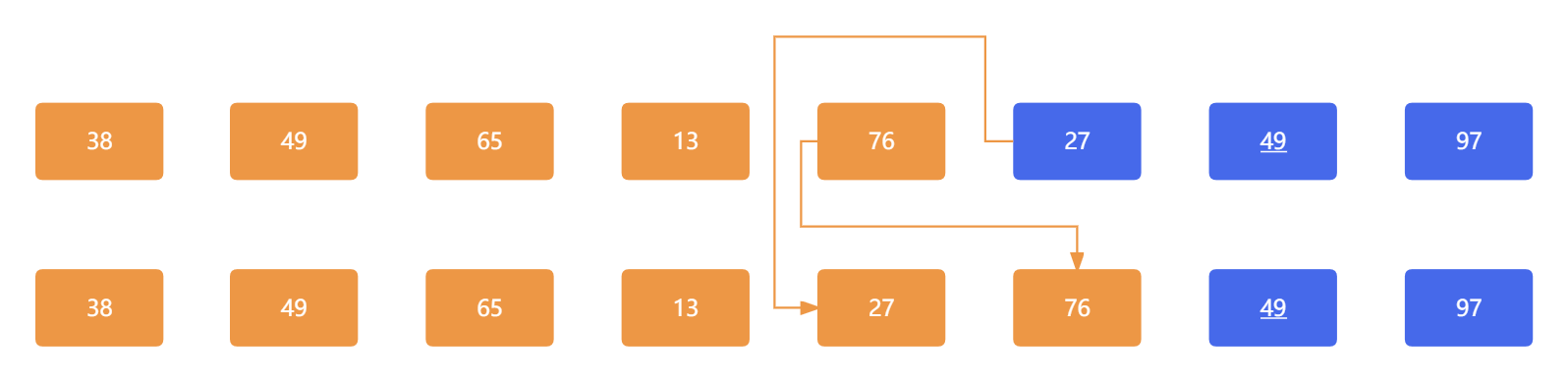
下一对元素 76 和 49 相比，因为 76 大于 49 ，所以两个元素需要交换彼此的位置，此时应为：

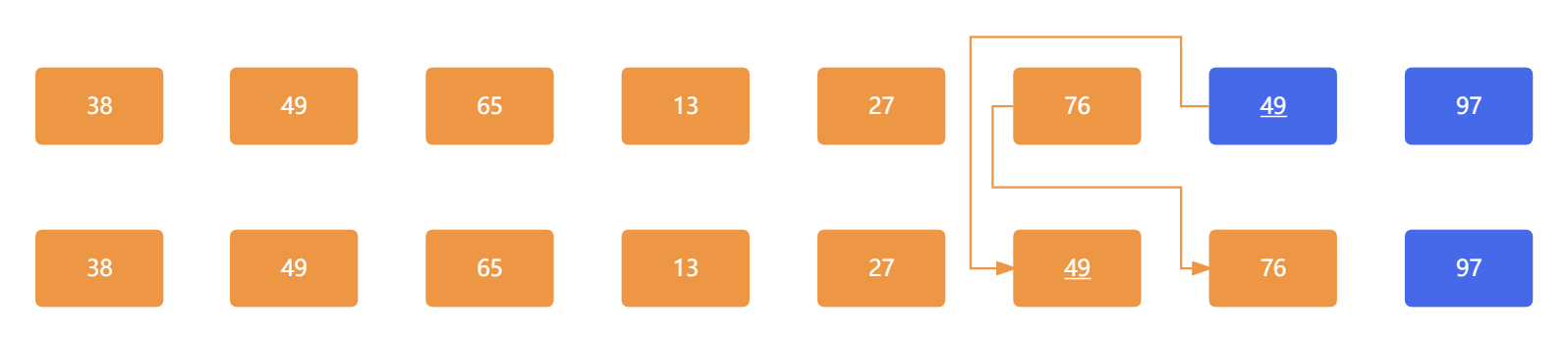
那么此时，我们第二趟也执行完毕，已将将 76 冒到了后面的位置，接下来继续执行下一次循环：

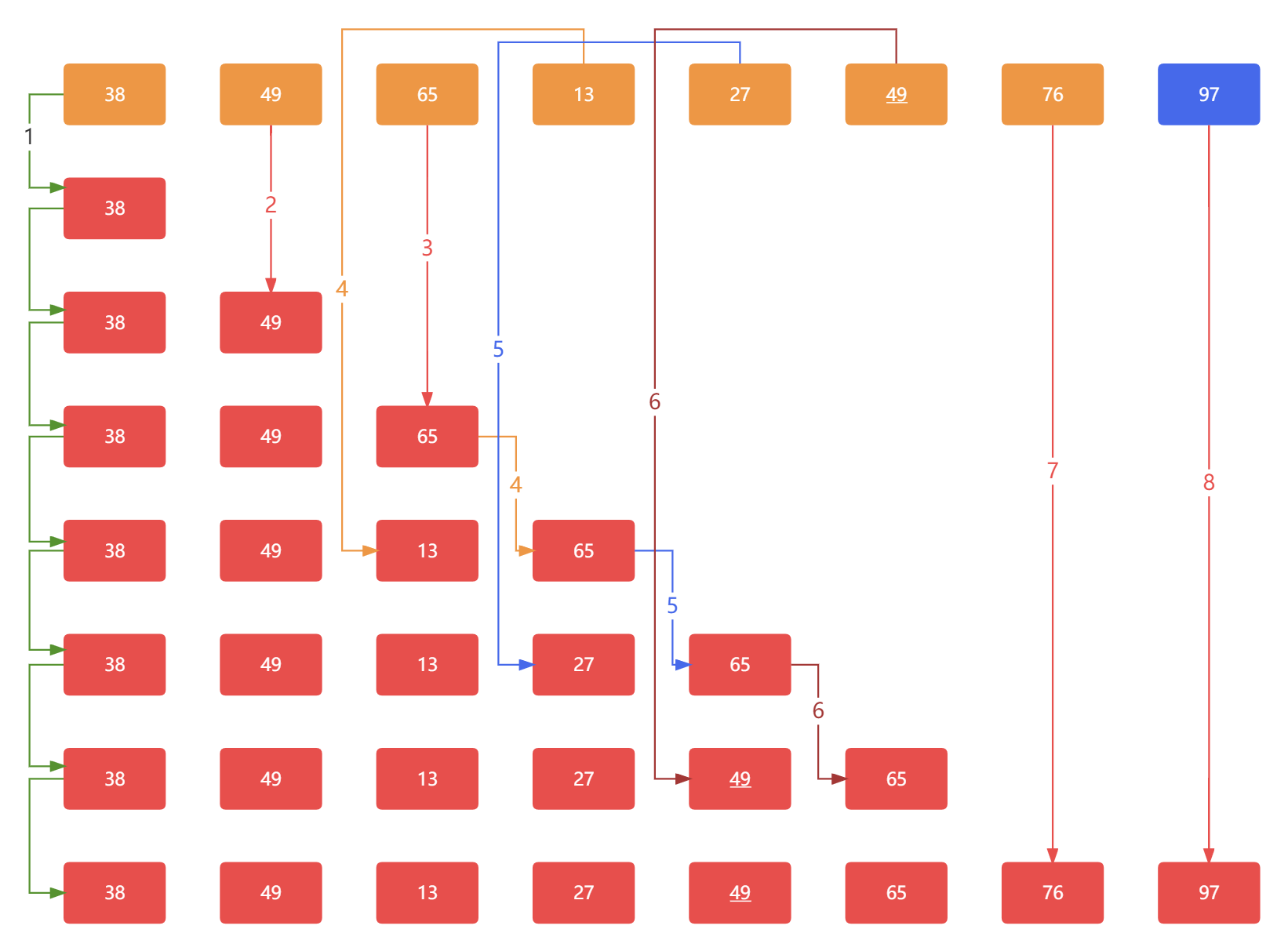
至此，第三趟循环已经完成，我们将 65 这个元素冒到了对应的位置，接下来继续重复之前的操作：

那么第四趟循环应该是将第一个出现的 49 向后进行位置交换，直到找到第二个 49 出现，停止循环，结果如下：

此时我们发现，其实下次循环过后，将 38 冒到 27 后面，就是一个有序的数组了，执行过程依旧如上，两两进行交换，那么第五趟循环的结果应为最终结果，数组元素排列次序如下：

至此，我们整个排序过程就结束了，可以看到， 49 和 49 排序前和排序后位置没有发生改变，所以我们说，冒泡排序也是一个稳定的排序，插帽龟嘛，都是稳定的。

代码示例（Java）

@Test
public void bubbleSort() {
    int[] arr = {49, 38, 65, 97, 76, 13, 27, 49};
    int n = arr.length - 1;
    for (int i=0; i<n; i++) {
        //如果左边大于右边则将他们调换位置
        for (int j = 0; j < n - i; j++) {
            if (arr[j] > arr[j + 1]) {
                arr[j] ^= arr[j + 1];
                arr[j + 1] ^= arr[j];
                arr[j] ^= arr[j + 1];
            }
        }
    }
}

冒泡排序特性总结

1. 冒泡排序是一种非常容易理解的排序

2. 时间复杂度：

   ​ 最坏情况 -> 数组逆序：O(N²) (双重循环，每轮排序要比较n次，并且重复n次)

   ​ 最好情况 -> 数组顺序：O(N)（最少得执行一次内层循环）

3. 空间复杂度：O(1)

4. 稳定性：稳定