从算法到算命—八大排序算法之希尔（shell）排序篇

从算法到算命—八大排序算法之希尔（shell）排序篇

核心思想

先将整个待排元素序列分割成若干个子表，对每一个子表进行直接插入排序

算法描述

希尔排序会先将整个待排序的记录序列分割成为若干子表分别进行直接插入排序，具体算法描述：

• 选择一个增量序列t₁，t₂，…，t_k，其中t_i > t_j，t_k=1；
• 按增量序列个数k，对序列进行k 趟排序；
• 每趟排序，根据对应的增量t_i，将待排序列分割成若干长度为m 的子表，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

动图演示

排序过程

是不是看完算法描述的你还是不太理解在说什么呢？毕竟解释的太官方，还是很难懂啦，接下来我会详细介绍排序过程，不过在此之前，我们需要先聊聊几个概念。

首先第一个是子表。我们还是先来构建一个数组，数据等同于之前的直接插入排序。

子表可以将其理解为将待排序的数据分成多个较小的部分。子表其实就是是原始数据序列的一部分，数组其中的元素被拆分后组成多个小数组。

第二个概念是步长（也成为增量），我们一般用字母d来表示，是指去欸的那个子表大小的规则或者序列。

以我们构建的数组为例，长度为8，我们取步长为4，就是将起始元素和起始元素上的指针向后移动四位所指向的元素放进同一个数组，然后将起始元素的指针后移，重复这个过程。

当d = 4时，我们得到如下子表：

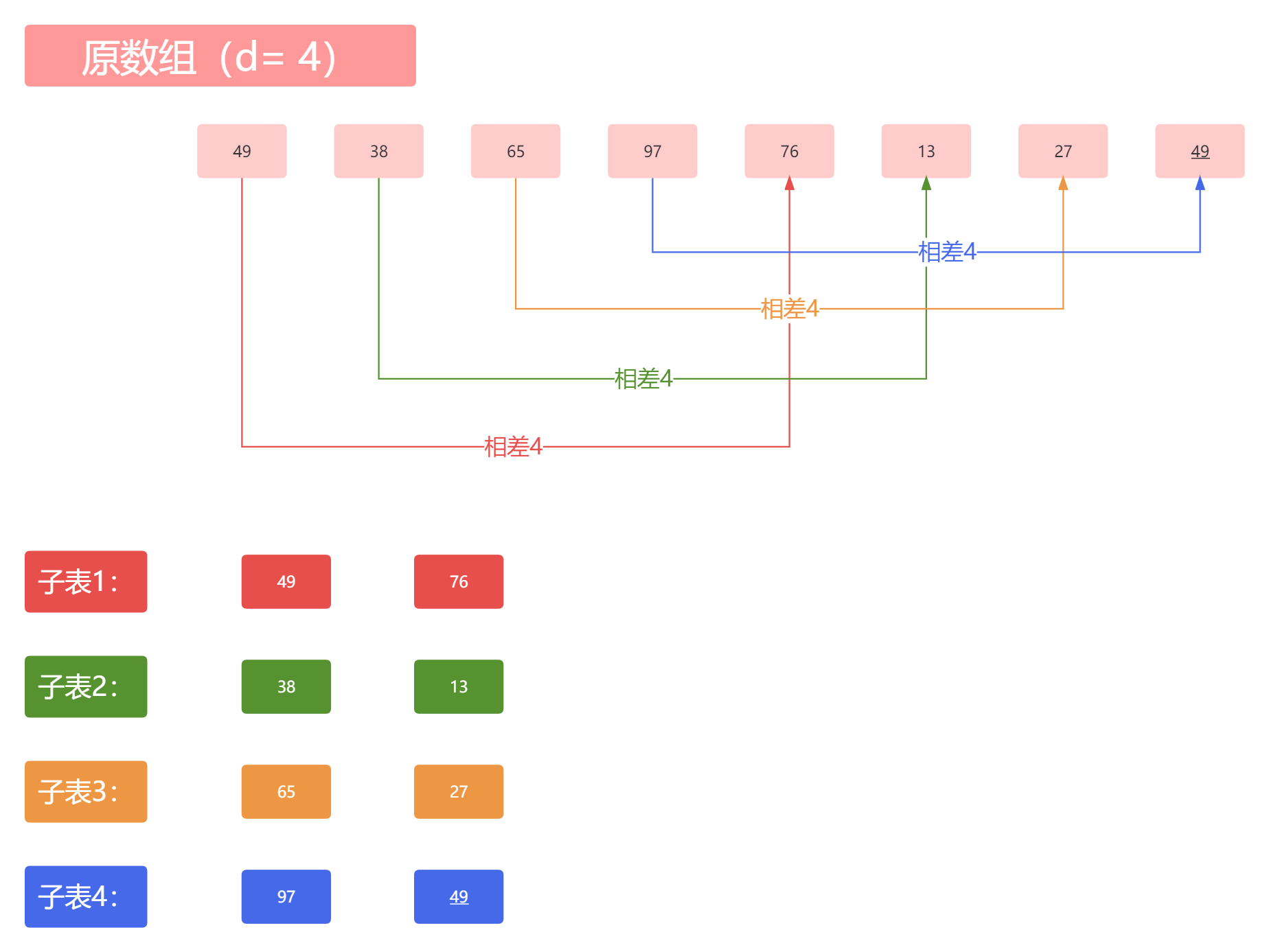
在我们得到子表后，对每一个子表进行直接插入排序，因为我们现在每个子表只有两个元素，所以相对排序并不是很复杂，只需要看条件是不是两两交换。为了方便查看，我将对应元素位置体现在下图中：

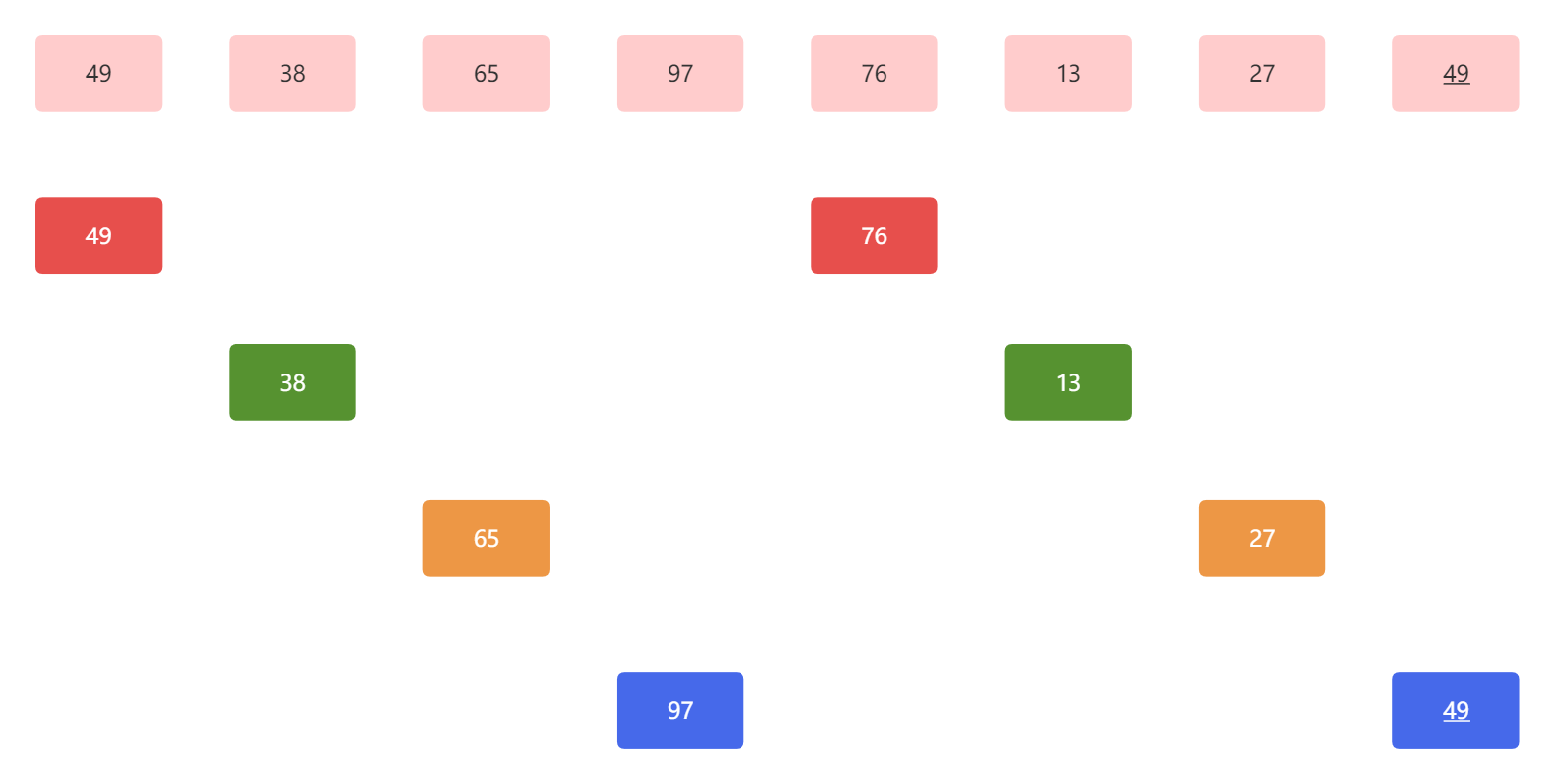
在这里，我们需要对子表进行插入排序，我们可以直接看出来。除了子表1中两个元素是有序的，其他子表都是无序的，也就是我们需要将子表2、3、4都进行排序。

那么在这里，有一个关键点，子表中直接插入排序，子表是连续存储的吗？当然是假的了，在这里，子表只是一个逻辑关系，也就是在逻辑上，每一个子表都是线性表，但是在物理上，它们该在哪个位置还在哪个位置。

那么第一趟我们得到的结果应该是这样的：

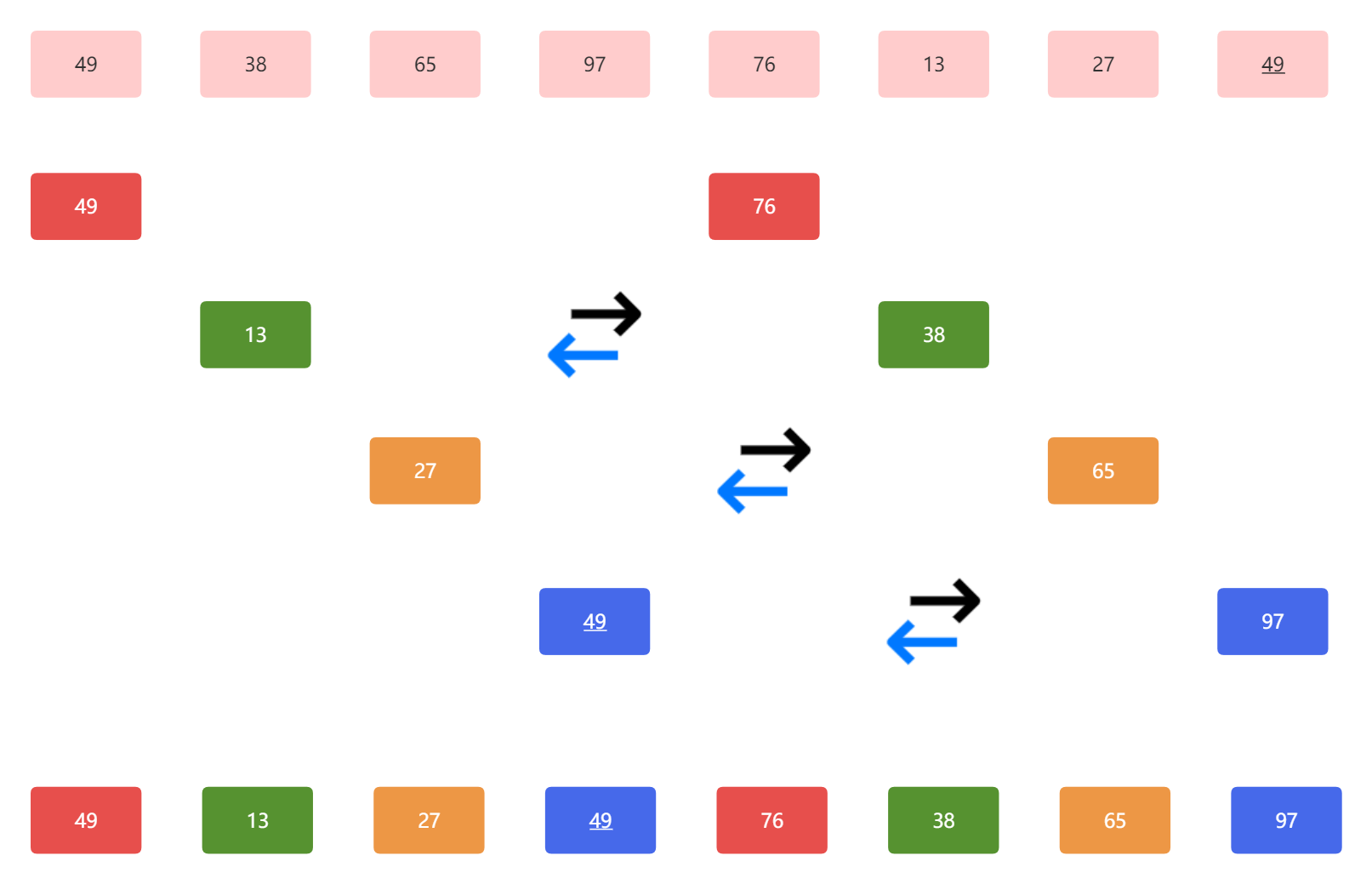
第二次我们再取步长的时候，一般取上一次步长的一半，也就是2。那么，我们拆分的子表应该是这样的：

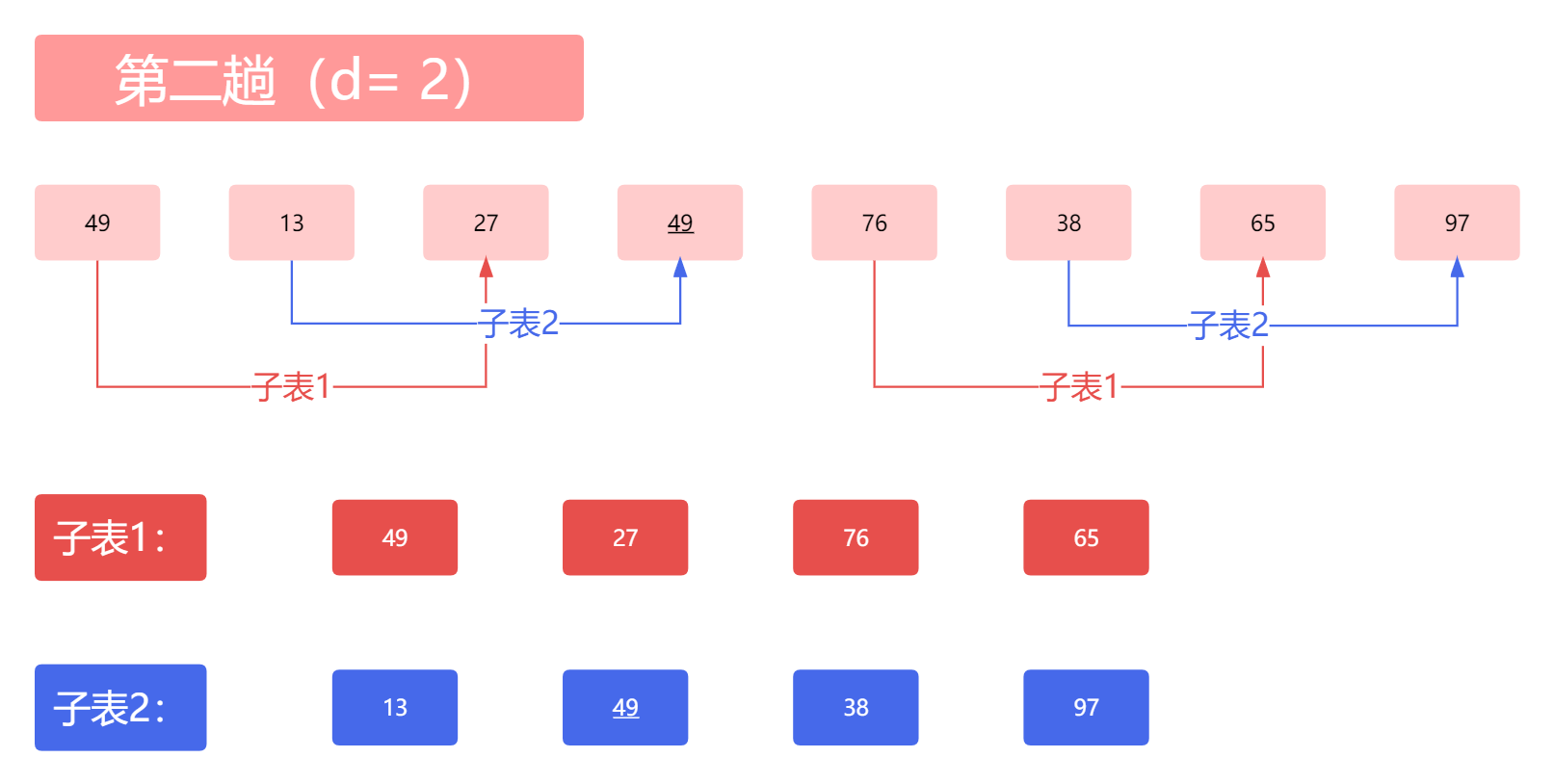
接下来我们对这两张子表进行直接插入排序，这里我图上稍微简化了一下步骤：

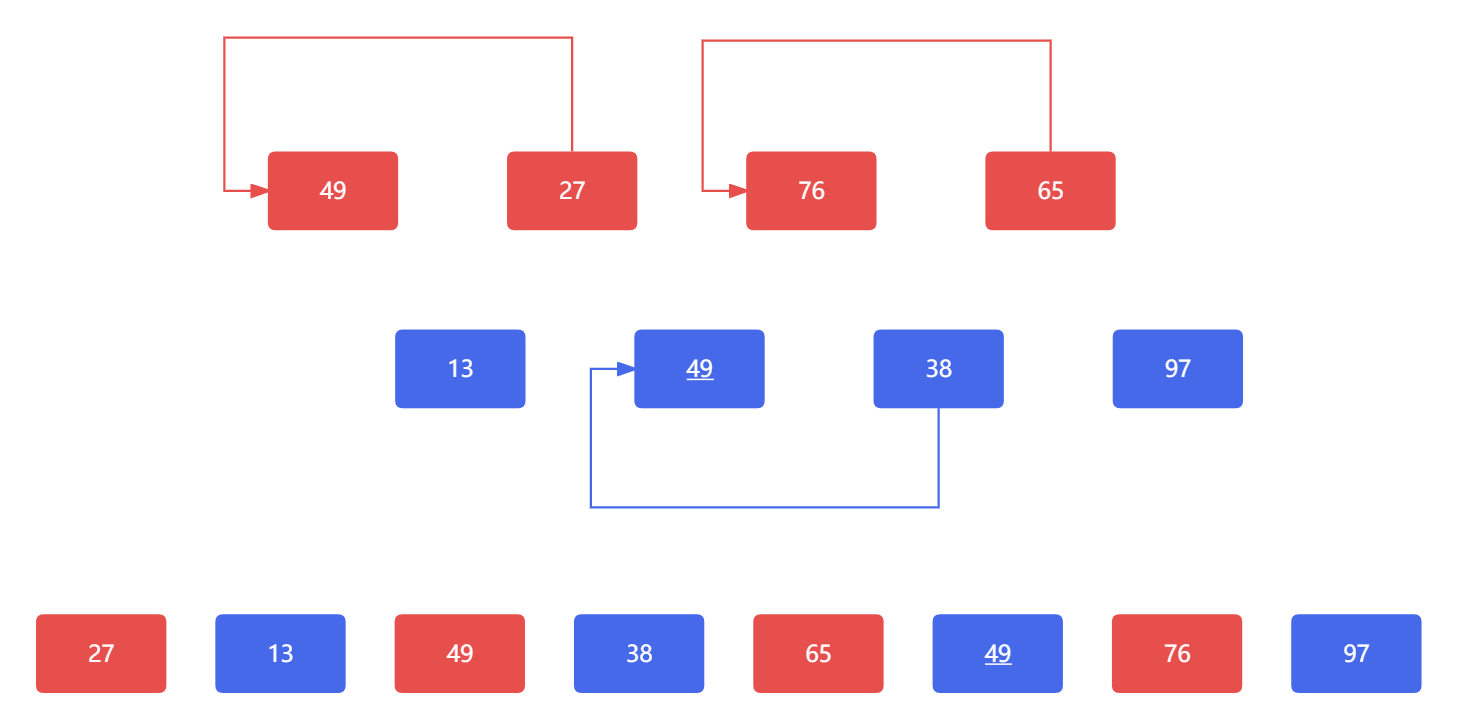
那么这时候，我们再次取步长的一半使得d = 1，这时候我们的数组就已经很接近有序了。当d = 1时，我们就不用继续细分子表了，这时候，我们实际上就是对一个数组进行直接插入排序，下图省略了部分过程，应该还是连续不断的直接插入排序的过程。

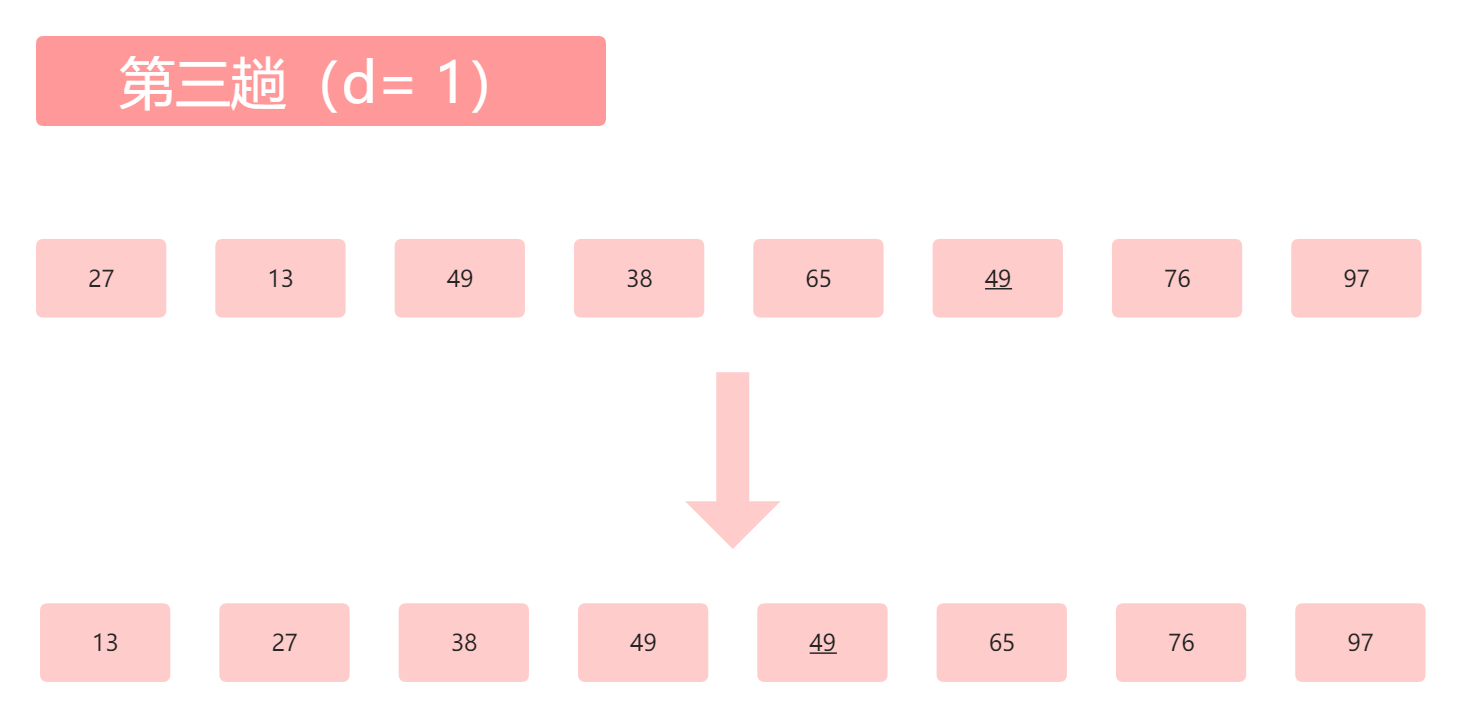
那么至此，我们已经通过希尔排序的方式将一个无序的数组变成了一个有序的数组，那么这里面有两个问题：

1. 步长的大小和预排序后的数据有什么关系？

   如果步长越小，数据跳跃越慢，但是子表排序后的数据就越接近有序；如果步长越大，大的数据可以更快的到达最后，小的数据可以更快的到达前面，但它越不接近有序，只能说是相对有序。

2. 希尔排序就一定比直接插入排序快吗？

   当所给数组本来就是升序或者接近升序的时候，进行拆分子表排序就相当于是无用功，相当于是白做的，此时的效率就不如直接插入排序了。当然，这种情况是很少的，一般所给的数据都是乱序或者接近逆序的，所以这种情况一般不去考虑。

代码示例（Java）

public void shellSort() {
        int[] arr = {49, 38, 65, 97, 76, 13, 27, 49};

        int n = arr.length;
        // 初始步长为数组长度的一半，逐步缩小步长
        for (int d = n >> 1; d > 0; d >>= 1) {
            // 对每个子表进行插入排序
            for (int i = d; i < n; i++) {
                int temp = arr[i];
                int j = i;
                // 在子表中进行插入排序
                while (j >= d && arr[j - d] > temp) {
                    arr[j] = arr[j - d];
                    j -= d;
                }
                arr[j] = temp;
            }
        }
    }

希尔排序特性总结

1. 希尔排序是对直接插入排序的优化。
2. 当d > 1时都是预排序，目的是让数组更接近于有序。当d == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。
3. 希尔排序的时间复杂度不好计算，因为d的取值方法很多，导致很难去计算，因此各个书中给出的希尔排序的时间复杂度都不固定。
4. 稳定性：不稳定