从算法到算命—八大排序算法之直接插入排序篇

从算法到算命—八大排序算法之直接插入排序篇

核心思想

和前面的相比，找到对应位置插入

算法描述

1. 从第一个元素开始，该元素可以认为已经被排序；
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描；
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置；
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
5. 将新元素插入到该位置后；
6. 重复步骤2~5。

动图演示

排序过程

本次我们演示的是升序，首先我们先来构建一个顺序表：

首先我们的指针指向第一个位置，也就是上图中对应的第一个元素 49 ，用 49 和前面比。这时候我们可以看到 49 前面并没有前面，它是第一个，那我们就把它拿下来，不管它。

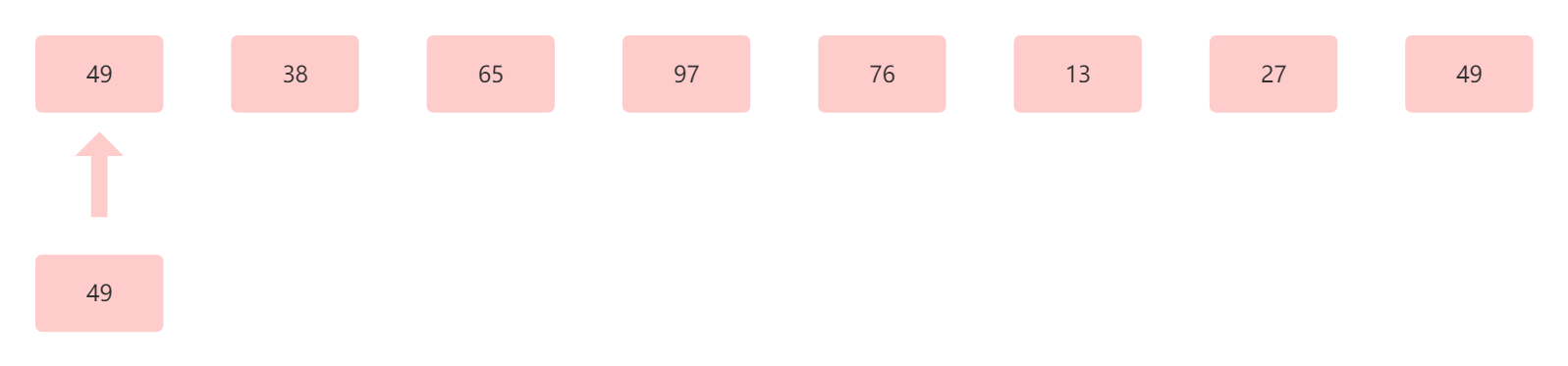
此时为第一趟，结果为49

接下来指针指向 38 ，用 38 和 49 比较，因为 38 比 49 小，所以把 38 插入到 49 前面

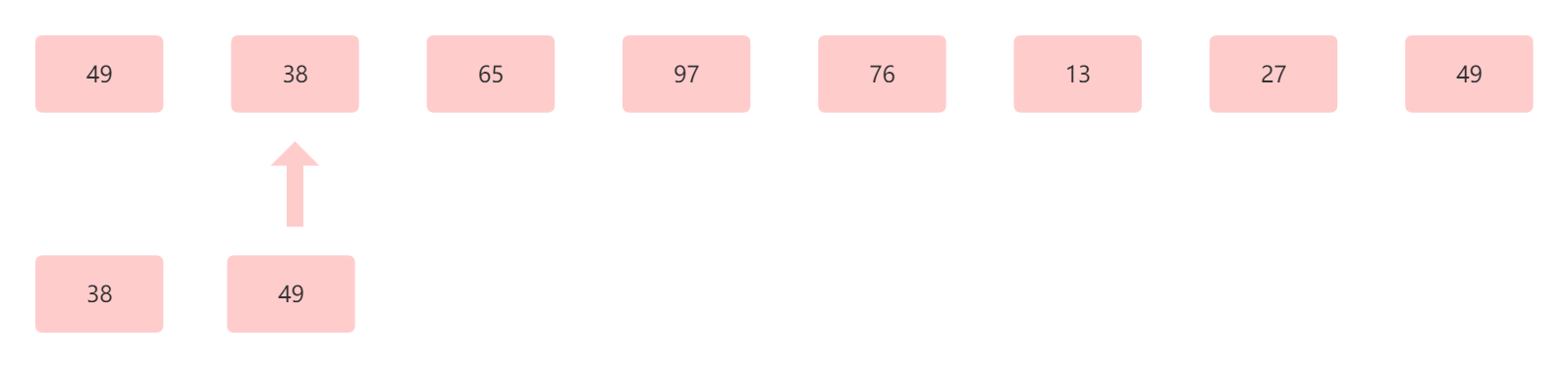
此时为第二趟，结果为38 49

指针继续后移，指针指向 65 ，因为 65 比前面两个值都大，所以不用改变位置，直接插入到原本的位置。

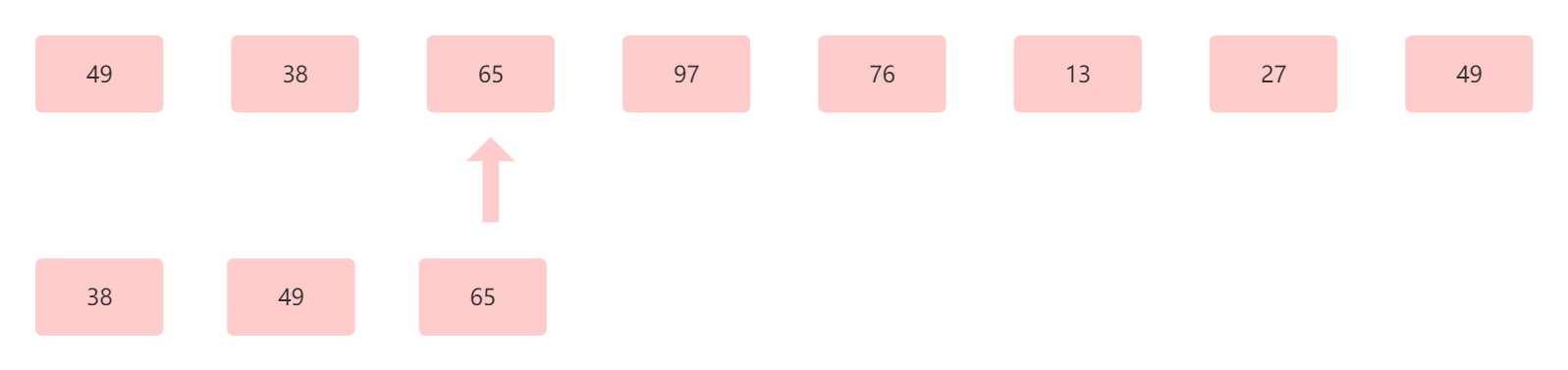
此时为第三趟，结果为 38 49 65

指针继续后移，指针指向 97 ，因为 97 比前面三个值都大，同理不用改变位置，直接插入到原本的位置。

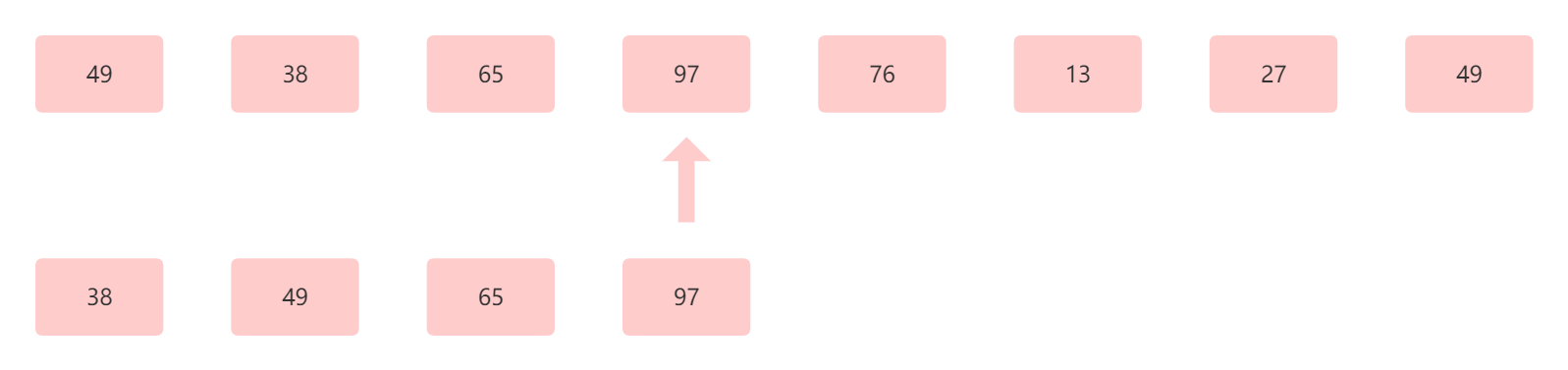
此时为第四趟，结果为38 49 65 97

指针再往后走，指向 76 ，我们希望 76 可以和前面排好序的数组再次组成有序数组，期望将 76 放在65 和 97 之间 ，所以我们应该让 76 插在 65 后面。

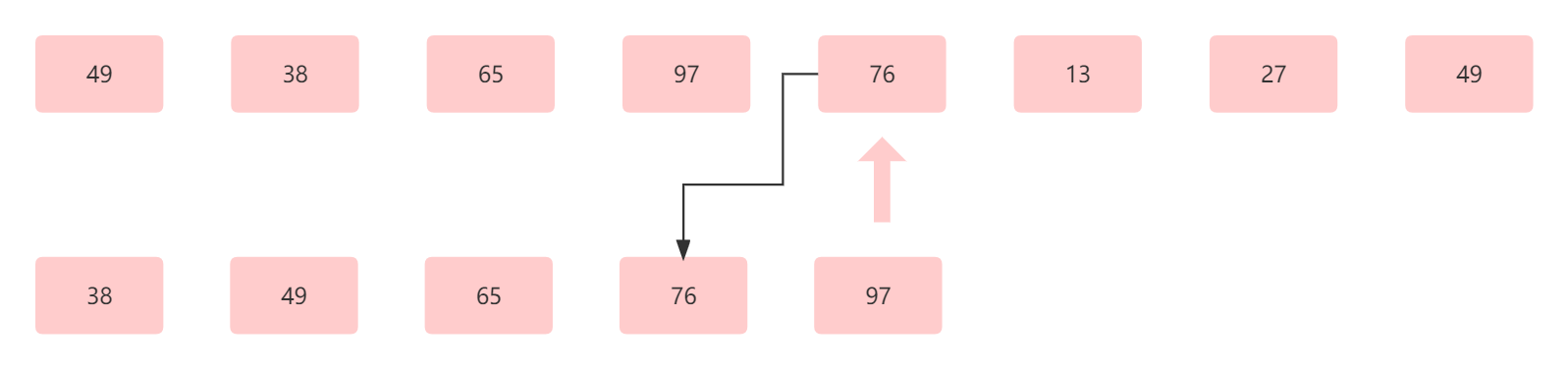
此时为第五趟，结果为38 49 65 76 97

指针再次后移，指向 13。我们希望将 13 插在最前面，因为其他元素都比 13 大。所以我们将该元素插入到最前面，形成有序数组。

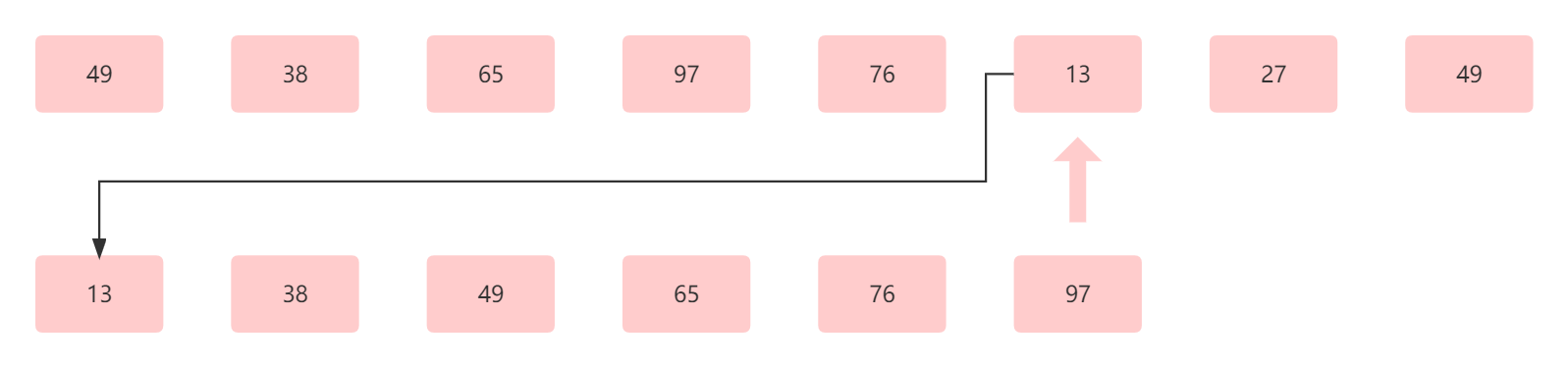
此时为第六趟，结果为13 38 49 65 76 97

再次移动指针，指向 27 ，此时如果我们想让插入后的数组形成有序数组，逻辑上应该插入到上个结果中 13和 38 之间。

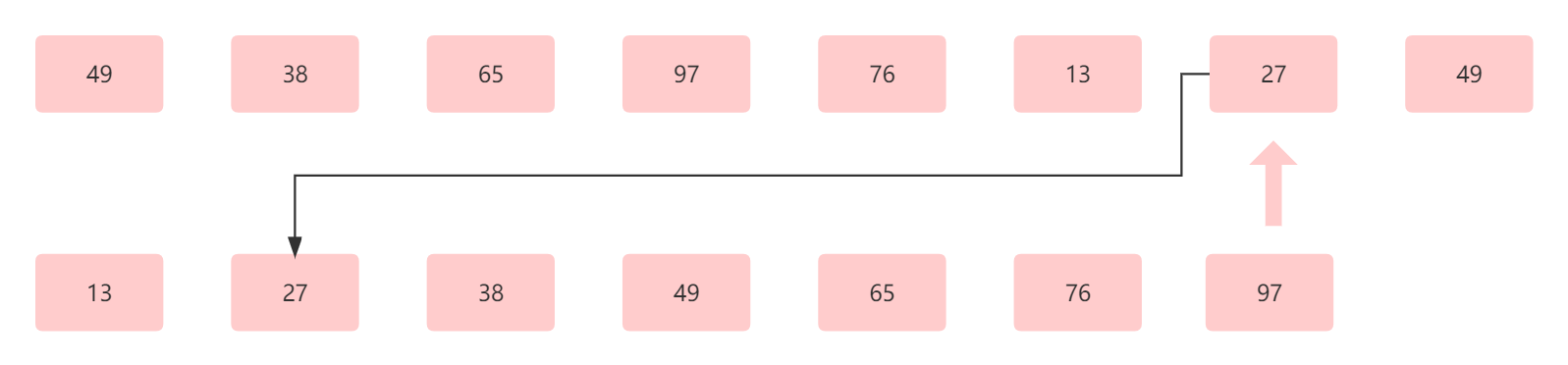
此时为第七趟，结果为 13 27 38 49 65 76 97

最后指针指向最后元素 49 ，此时我们发现，这个数组中有重复的元素 49，那么此时问题来了，我们应该插入到排好序的 49 之前还是之后呢？

我们以上一个结果举例，当我们将 27 插入到对应位置后，实际上还要执行将后面所有元素后移的操作，就是将从 38 起至 97 的元素都往后移动一个位置。那么插入 49 的时候也是同理，我们来看。如果插入在第一个出现位置的前面，我们需要移动 49 、65 、76 、97 这四个元素。而如果我们插入至第一个出现的位置后面，则只需要移动 65 、 76 、97 这三个元素。

我们设计算法的目的当让是越简单越好，在这里体现就是移动个数越少越好。所以我们将 49 插入至上一个 49之后。

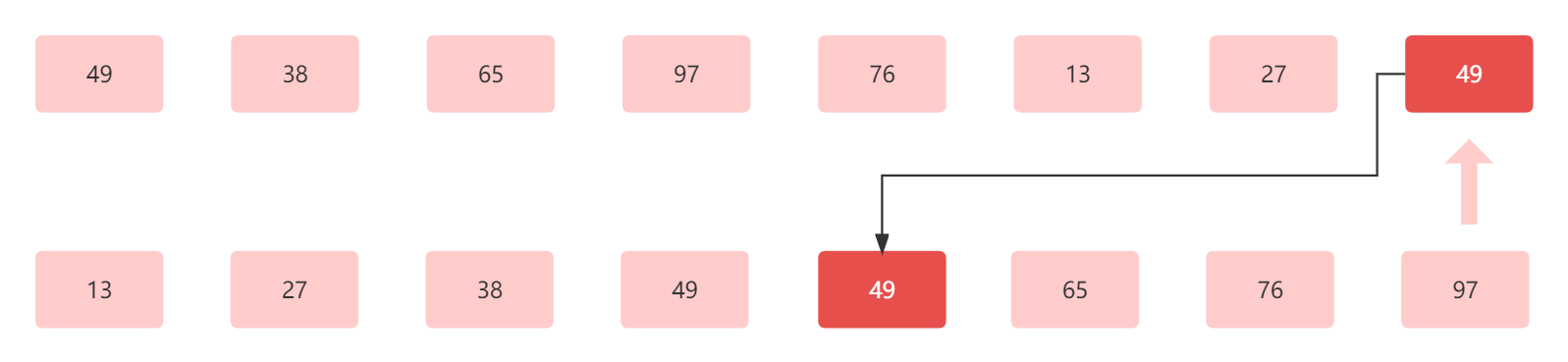
此时为第八趟，最后的结果为13 27 38 49 49 65 76 97

那么到此为止，本次排序就完成了，由于存在相同的元素 49 ，并且相对顺序在排序后没有发生变化，所以我们说插入排序是一个稳定的排序。

代码示例(Java)

//传统写法
public void insertinoSort() {
        int[] array = {49, 38, 65, 97, 76, 13, 27, 49};
        int n = array.length;
        for (int i = 1; i < n; i++) {
            int key = array[i];
            int j = i - 1;

            // 将数组分为已排序和未排序两部分，将未排序的元素逐个插入到已排序的部分中
            // 在每次迭代中，将当前元素存储在key变量中
            // 将已排序部分中比key大的元素向右移动一个位置，直到找到合适的位置插入key

            while (j >= 0 && array[j] > key) {
                array[j + 1] = array[j];
                j--;
            }
            array[j + 1] = key;
        }
        for (int i : array) {
            System.out.println(i);
        }
    }

除了这种写法之外，我们可以用异或（^）交换操作来替代插入操作

//异或交换写法
public void swapInsertinoSort() {
        int[] array = {49, 38, 65, 97, 76, 13, 27, 49};
        int n = array.length;
        for (int i = 1; i < n; i++) {
            while (i > 0 && array[i - 1] > array[i]) {
                // 使用异或来交换元素的值
                array[i] ^= array[i - 1];
                array[i -1] ^= array[i];
                array[i] ^= array[i-1];
                i--;
            }
        }
        for (int i : array) {
            System.out.println(i);
        }
    }

小知识：异或操作满足交换律，所以可以通过 a ^= b, b ^= a, a ^= b来实现a与b值的交换。

直接插入排序特性总结

1. 元素集合越接近有序，直接插入排序算法的时间效率越高
2. 时间复杂度：
   • 最坏的情况（逆序）：比较次数是 1 + 2 + 3 + ... + (N - 1)
     • 时间复杂度：O(N²)
   • 最好的情况（有序）：每插入一个元素，只需要考查前一个元素
     • 时间复杂度：O(N)
3. 空间复杂度：O(1)，它是一种稳定的排序算法
4. 稳定性：稳定