二叉查找树

概念与定义

一棵二叉查找树是一棵二叉树，其中每个节点都含有一个键（以及相关联的值，即key-value对），

且每个节点的键都大于其左子树中任意节点的键而小于其右子树中任意节点的键。

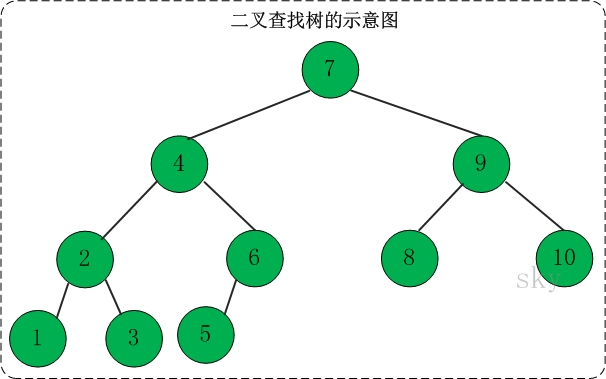
（图中数字表示节点的键，由于键的唯一性，后续内容皆用键代指节点）

 

 

 节点的定义

 二叉树中的一个节点应当包含，一个键、一个值、一个左链接、一个右链接及一个计数器。

计数器表示以该节点为根的二叉树所含有的节点总个数，则整个二叉树的节点总数则为根节点计数器的值。

    // 定义根节点
    private class Node {
        private Key key;
        private Value val;
        private int N;
        private Node left, right;

        public Node (Key key, Value val, int N) {
            this.key = key;
            this.val = val;
            this.N = N;
        }
    }

 

 

二叉树的大小（即包含节点的总个数）

由于每个节点都包含一个计数器，则整个二叉树的节点总数则为根节点计数器的值。

 

    // 二叉树的大小
    public int size() {
        return size(root);
    }
    private int size(Node x) {
        if (x == null) return 0;
        else return x.N;
    }

 

 

查找（有键key找到对应的值val）

 根据键key查找对应的值val是一个递归过程：

如果节点是空的，则查找未命中；

如果节点的键与被查找的键相同，查找命中；

如果被查找的键较小，选择节点的左子树，否则右子树。

 

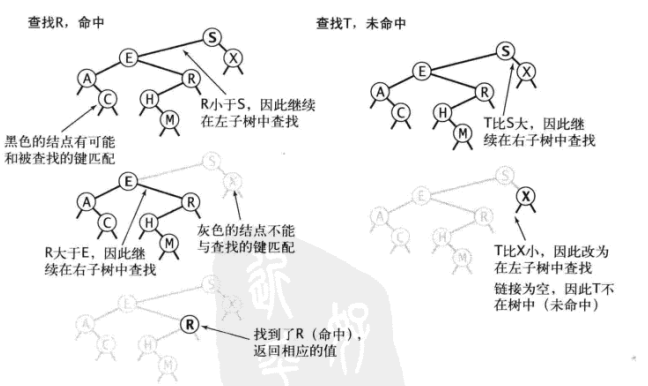
    // 查找
    public Value get(Key key) {
        return get(root, key);
    }
    private Value get(Node x, Key key) {
        if (x == null) return null;
        int cmp = key.compareTo(x.key);
        if (cmp > 0) return get(x.right, key);
        else if (cmp < 0) return get(x.left, key);
        else return x.val;
    }

查找算法的复杂度：2lnN 约为1.39logN

 

 

 

插入（向二叉树中插入一个键-值对）

插入操作与查找类似：

若果节点为空，以待插入键-值生成一个新的节点；

节点的键等于待插入的键，节点的值更新为待插入的值；

节点的键大于待插入的键，向节点的左子树中插入该键；

节点的键小于待插入的键，向节点的右子树中插入该键；

 

    // 向二叉树中插入1个键-值对
    public void put(Key key, Value val) {
        root = put(root, key, val);
    }
    private Node put(Node x, Key key, Value val) {
        if (x == null) return new Node(key, val, 1);

        int cmp = key.compareTo(x.key);
        if (cmp > 0) x.right = put(x.right, key, val);
        else if (cmp < 0) x.left =  put(x.left, key, val);
        else x.val = val;
        x.N = size(x.left) + size(x.right) + 1;
        return x;
    }

 

 

 最大键与最小健

有二叉查找树的特性可知，最大键即是最右端节点的键，最小健即是最左端节点的键。

 

    // 最小健
    public Key min() {
        return min(root).key;
    }
    private Node min(Node x) {
        if (x.left == null) return x;
        return min(x.left);
    }

    // 最大键
    public Key max() {
        return max(root).key;
    }
    private Node max(Node x) {
        if (x.right == null) return x;
        return max(x.right);
    }

 

 

 

删除最大键与最小健

 删除最小健：用最小健的右链接（为节点或null）替换最小健，同时将最小健的右链接改为null。

删除最大键：用最大键的左链接替换最大键，同时将最大键的左链接改为null。

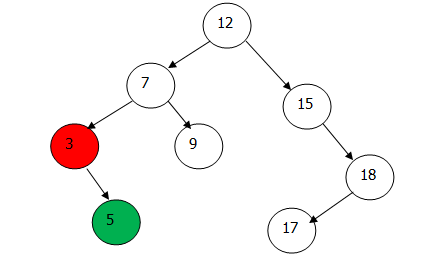
二叉查找树中，最小健为3，用其右链接节点5替换节点3，则完成最小健的删除。

 

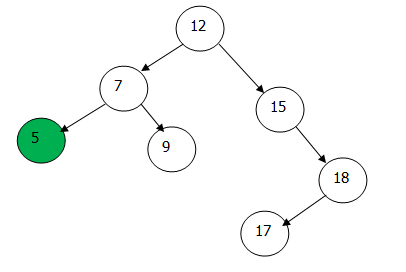
    // 删除最小健
    public void deleteMin() {
        root = deleteMin(root);
    }
    private Node deleteMin(Node x) {
        if (x.left == null) {
            Node temp = x.right;
            x.right = null;
            return temp;
        }
        x.left = deleteMin(x.left);
        x.N = size(x.left) + size(x.right) + 1;
        return x;
    }


    // 删除最大键
    public void deleteMax() {
        root = deleteMax(root);
    }
    private Node deleteMax(Node x) {
        if (x.right == null) {
            Node temp = x.left;
            x.left = null;
            return temp;
        }
        x.right = deleteMax(x.right);
        x.N = size(x.left) + size(x.right) + 1;
        return x;
    }

 

 

 

删除键

 根据给定的键删除二叉查找树中的节点。

设待删除的键为节点temp，若temp的左链接或右链接为null，则删除方法与删除最大键/最小健的方法相同。

 

需要注意的则是temp的左右链接均不为空（null）的情况。

用temp右链接中的最小键节点替换temp，这样替换后仍满足二叉查找树的性质。

    // 删除键
    public void delete(Key key) {
        root = delete(root, key);
    }
    private Node delete(Node x, Key key) {
        if (x == null) return null;

        int cmp = key.compareTo(x.key);
        if (cmp > 0) x.right = delete(x.right, key);
        else if (cmp < 0) x.left = delete(x.left, key);
        else {

            if (x.left == null) {
                Node temp = x.right;
                x.right = null;
                return temp;
            }
            if (x.right == null) {
                Node temp = x.left;
                x.left = null;
                return temp;
            }
            Node t = x;
            x = min(t.right);
            x.right = deleteMin(t.right);
            x.left = t.left;
        }
        x.N = size(x.left) + size(x.right) + 1;
        return x;
    }

 

 

 

二查找树的实现代码

public class BST<Key extends Comparable<Key>, Value> {

    // 定义节点
    private class Node {
        private Key key;
        private Value val;
        private int N;
        private Node left, right;

        public Node (Key key, Value val, int N) {
            this.key = key;
            this.val = val;
            this.N = N;
        }
    }


    // 根节点
    private Node root;

    // 二叉树的大小
    public int size() {
        return size(root);
    }
    private int size(Node x) {
        if (x == null) return 0;
        else return x.N;
    }

    // 查找
    public Value get(Key key) {
        return get(root, key);
    }
    private Value get(Node x, Key key) {
        if (x == null) return null;
        int cmp = key.compareTo(x.key);
        if (cmp > 0) return get(x.right, key);
        else if (cmp < 0) return get(x.left, key);
        else return x.val;
    }


    // 向二叉树中插入1个键-值对
    public void put(Key key, Value val) {
        root = put(root, key, val);
    }
    private Node put(Node x, Key key, Value val) {
        if (x == null) return new Node(key, val, 1);

        int cmp = key.compareTo(x.key);
        if (cmp > 0) x.right = put(x.right, key, val);
        else if (cmp < 0) x.left =  put(x.left, key, val);
        else x.val = val;
        x.N = size(x.left) + size(x.right) + 1;
        return x;
    }



    // 最小健
    public Key min() {
        return min(root).key;
    }
    private Node min(Node x) {
        if (x.left == null) return x;
        return min(x.left);
    }

    // 最大键
    public Key max() {
        return max(root).key;
    }
    private Node max(Node x) {
        if (x.right == null) return x;
        return max(x.right);
    }


    // 删除最小健
    public void deleteMin() {
        root = deleteMin(root);
    }
    private Node deleteMin(Node x) {
        if (x.left == null) {
            Node temp = x.right;
            x.right = null;
            return temp;
        }
        x.left = deleteMin(x.left);
        x.N = size(x.left) + size(x.right) + 1;
        return x;
    }


    // 删除最大键
    public void deleteMax() {
        root = deleteMax(root);
    }
    private Node deleteMax(Node x) {
        if (x.right == null) {
            Node temp = x.left;
            x.left = null;
            return temp;
        }
        x.right = deleteMax(x.right);
        x.N = size(x.left) + size(x.right) + 1;
        return x;
    }



    // 删除键
    public void delete(Key key) {
        root = delete(root, key);
    }
    private Node delete(Node x, Key key) {
        if (x == null) return null;

        int cmp = key.compareTo(x.key);
        if (cmp > 0) x.right = delete(x.right, key);
        else if (cmp < 0) x.left = delete(x.left, key);
        else {

            if (x.left == null) {
                Node temp = x.right;
                x.right = null;
                return temp;
            }
            if (x.right == null) {
                Node temp = x.left;
                x.left = null;
                return temp;
            }
            Node t = x;
            x = min(t.right);
            x.right = deleteMin(t.right);
            x.left = t.left;
        }
        x.N = size(x.left) + size(x.right) + 1;
        return x;
    }


}