二叉堆

二叉堆即是完全二叉树实现的堆，在二叉堆中每个节点总是大于等于其任意一个子节点。根结点是二叉堆中最大的节点。

 

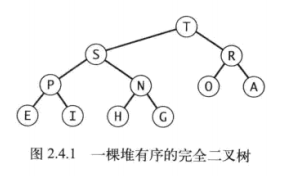
数组实现二叉堆

完全二叉树可以用数组实现，根结点的位置为1，其子节点为2、3。位置为k的节点，其两个子节点位置为2k、2k+1 。同理，位置为k的节点，其父节点的位置为k/2 。

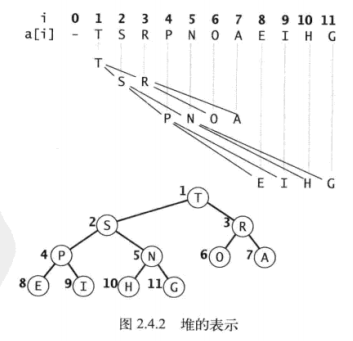
算法实现

使用长度为N+1的数组key[]来表示一个大小为N的堆，不使用key[0]，变量N用以记录堆的大小。

 

由下至上的堆有序化（上浮）

若某个子节点的值大于其父节点的值，可以通过交换该节点与父节点，使二叉堆有序。

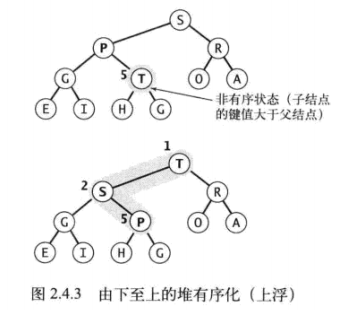
图中，节点5的键值为T大于其父节点键值P，交换后仍大于其父节点键值S，继续交换。

 

上浮实现代码如下：

    private void swim(int k) {

        int temp;
        // k>1,k不是根结点
        // 若k节点的键值大于其父节点键值，则交换
        while (k>1 && key[k]>key[k/2]) {
            temp = key[k];
            key[k] = key[k/2];
            key[k/2] = temp;

            k = k/2;
        }
    }

 

由上至下的堆有序化（下沉）

若某个节点的键值小于其子节点的键值，交换该节点与其子节点可使堆保持有序

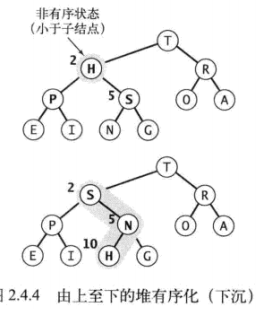
    private void sink(int k) {

        int temp;
        while (2*k <= N) {

            int j = 2*k;
            // 节点k有两个子节点：节点2k与节点2k+1
            // 选择两个子节点中键值较大的一个
            if (j < N && key[j] < key[j+1]) j++;
            if (key[j] < key[k]) break;
            temp = key[k];
            key[k] = key[j];
            key[j] = temp;
            k = j;
        }
    }

 

插入元素

 将新元素添加到数组的末尾，使用上浮swim()方法将该元素上浮到合适的位置。

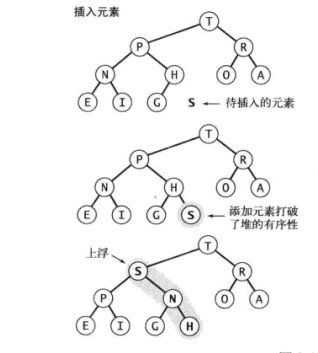
    public void insert(int k) {
        key[++N] = k;
        swim(N);
    }

 

删除最大的元素

二叉堆的根结点即数组的第一个元素为键值最大的元素，将数组的最后一个元素key[N]与key[1]交换，使用sink()方法，将该元素下沉到合适的位置。

    public int delMax() {

        int max = key[1];
        key[1] = key[N];
        key[N] = 0;
        N--;
        sink(1);
        return max;
    }

 

整个程序的代码如下：

import java.util.Arrays;

public class BinaryStack {

    // Complete binary tree based on array
    private int[] key;
    private int N = 0;

    public BinaryStack(int maxN) {

        key = new int[maxN+1];
    }

    // Insert a key into the tree
    public void insert(int k) {
        key[++N] = k;
        swim(N);
    }

    // Delete the  maximum  key from the tree
    public int delMax() {

        int max = key[1];
        key[1] = key[N];
        key[N] = 0;
        N--;
        sink(1);
        return max;
    }

    private void swim(int k) {

        int temp;
        // k>1,k不是根结点
        // 若k节点的键值大于其父节点键值，则交换
        while (k>1 && key[k]>key[k/2]) {
            temp = key[k];
            key[k] = key[k/2];
            key[k/2] = temp;

            k = k/2;
        }
    }

    private void sink(int k) {

        int temp;
        while (2*k <= N) {

            int j = 2*k;
            // 节点k有两个子节点：节点2k与节点2k+1
            // 选择两个子节点中键值较大的一个
            if (j < N && key[j] < key[j+1]) j++;
            if (key[j] < key[k]) break;
            temp = key[k];
            key[k] = key[j];
            key[j] = temp;
            k = j;
        }
    }



    public static void main(String[] args) {

        BinaryStack stack = new BinaryStack(20);
        stack.insert(8);
        stack.insert(12);
        stack.insert(3);
        stack.insert(7);
        stack.insert(10);
        stack.insert(9);
        stack.insert(6);

        System.out.println(Arrays.toString(stack.key));
    }
}

 

算法复杂度