快速排序

将一个数组分成两个子数组，子数组1的元素都小于等于v，子数组2的元素都大于等于v，v可取值为数组中的任意元素。

在分别对子数组进行上述排序，直到子数组的元素个数为1，整个数组排序完成。

 

数组切分

该算法的关键在于数组切分，即选取切分元素v，使子数组1的元素都小于等于v，子数组2的元素都大于等于v。

以下示例选取数组中的第一个元素a[lo]为切分元素

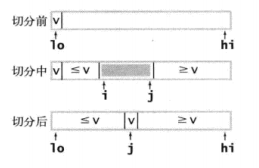
实现代码如下：

    public static int partision(int[] a, int lo, int hi) {

        
        int i = lo+1;
        int j = hi;
        int v = a[lo];
        while(true) {

            // 从左向右扫描，寻找大于v的元素
            while(i<=j && a[i]<=v) i++;
            // 从右向左扫描，寻找小于v的元素
            while(i<=j && a[j]>=v) j--;

            // 交换a[i]与a[j]
            if(i<j) {
                int temp = a[i];
                a[i] = a[j];
                a[j] = temp;
            }
            // 若i>=j，扫描完成
            // 交换a[lo]与a[j]
            else {
                int temp = a[lo];
                a[lo] = a[j];
                a[j] = temp;
                return j;
            }
        }
    }

递归方法可实现整个快速排序，如下：

    public static void sort(int[] a, int lo, int hi) {

        if(hi<=lo) return;
        int j = partision(a, lo, hi);
        sort(a, lo, j-1);
        sort(a, j+1, hi);
    }

    public static void sort(int[] a) {

        sort(a, 0, a.length-1);
    }