希尔排序

以下转自http://www.cnblogs.com/skywang12345/p/3597597.html

 

算法内容：

对于n个待排序的数列，取一个小于n的整数gap(gap被称为步长)将待排序元素分成若干个组子序列，所有距离为gap的倍数的元素放在同一个组中；然后，对各组内的元素进行直接插入排序。 这一趟排序完成之后，每一个组的元素都是有序的。然后减小gap的值，并重复执行上述的分组和排序。重复这样的操作，当gap=1时，整个数列就是有序的。

 

示例如下：

以数列{80,30,60,40,20,10,50,70}为例，演示它的希尔排序过程

gap=4

当gap=4时,意味着将数列分为4个组： {80,20},{30,10},{60,50},{40,70}。 对应数列：{80,30,60,40,20,10,50,70}
对这4个组分别进行排序，排序结果： {20,80},{10,30},{50,60},{40,70}。 对应数列： {20,10,50,40,80,30,60,70}

 

第2趟：(gap=2)

 

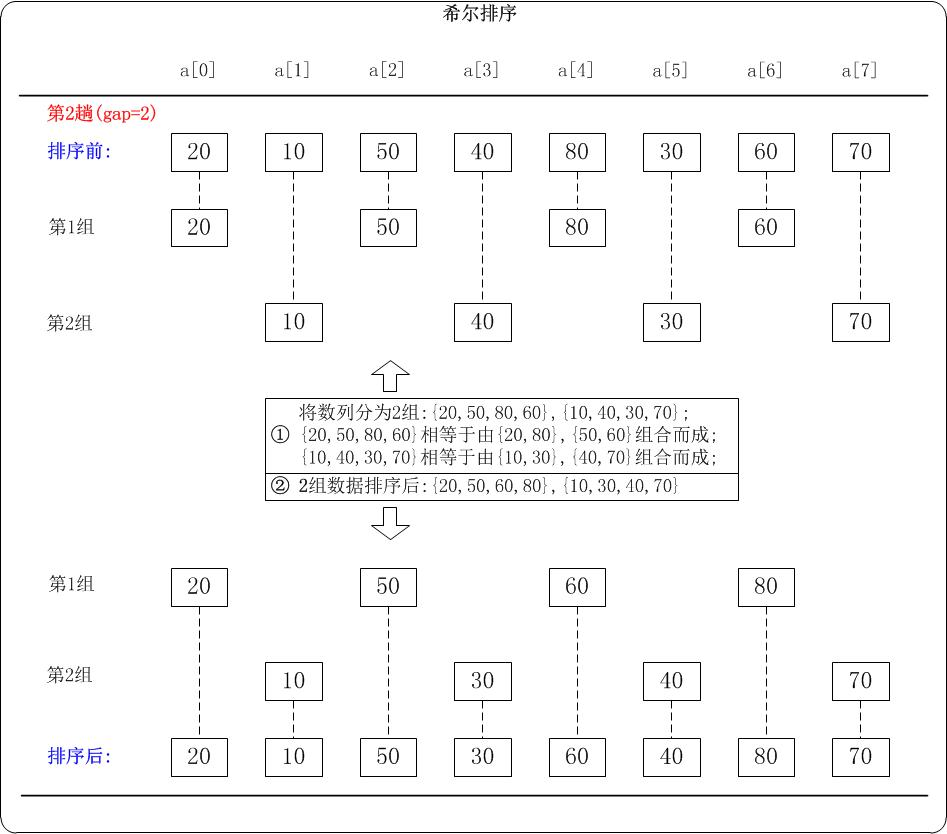
当gap=2时,意味着将数列分为2个组：{20,50,80,60}, {10,40,30,70}。 对应数列： {20,10,50,40,80,30,60,70}
注意：{20,50,80,60}实际上有两个有序的数列{20,80}和{50,60}组成。
          {10,40,30,70}实际上有两个有序的数列{10,30}和{40,70}组成。
对这2个组分别进行排序，排序结果：{20,50,60,80}, {10,30,40,70}。 对应数列： {20,10,50,30,60,40,80,70}

 

第3趟：(gap=1)

 

当gap=1时,意味着将数列分为1个组：{20,10,50,30,60,40,80,70}
注意：{20,10,50,30,60,40,80,70}实际上有两个有序的数列{20,50,60,80}和{10,30,40,70}组成。
对这1个组分别进行排序，排序结果：{10,20,30,40,50,60,70,80}

 

 

 

 

希尔排序时间复杂度
希尔排序的时间复杂度与增量(即，步长gap)的选取有关。例如，当增量为1时，希尔排序退化成了直接插入排序，此时的时间复杂度为O(N²)，而Hibbard增量的希尔排序的时间复杂度为O(N^3/2)。

希尔排序稳定性
希尔排序是不稳定的算法。

如数列（2,9,6,6），取gap=2，则排序后为（2,6,6,9），原数列中第三个6位于第二个6之前。

算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

 

代码实现：

    private static void shellSort(int[] nums) {

        int gap = 1;
        while (gap < nums.length/3) gap = 3 * gap + 1;

        int temp;
        while (gap >= 1) {

            for (int i=gap; i<nums.length; i++)
                for (int j=i; j>=gap && nums[j]<nums[j-gap]; j-=gap) {
                    temp = nums[j];
                    nums[j] = nums[j-gap];
                    nums[j-gap] = temp;
                }
            gap = gap / 3;
        }
    }