https://blog.csdn.net/newworld123made/article/details/51449739
施密特正交化的几何解释
线性代数中最头疼的公式恐怕就是施密特正交化了。但其实搞清楚它的几何原理之后公式的记忆就简单多了,数学重在理解!
给定一组基α1,α2,...,αnα1,α2,...,αn,将其变换成另外一组正交基β1,β2,...,βnβ1,β2,...,βn,使这两组基等价
施密特正交化方法:
β1=α1β1=α1
β2=α2−(α2,β1)(β1,β1)β1β2=α2−(α2,β1)(β1,β1)β1
…
βn=αn−(αn,β1)(β1,β1)β1−(αn,β2)(β2,β2)β2−...−(αn,βn−1)(βn−1,βn−1)βn−1βn=αn−(αn,β1)(β1,β1)β1−(αn,β2)(β2,β2)β2−...−(αn,βn−1)(βn−1,βn−1)βn−1
首先清除一个公式,两个向量α,βα,β,那么αα在ββ上的投影向量为(α,β)(β,β)β(α,β)(β,β)β
如图红色部分即为投影部分
则蓝色部分向量为α2−(α2,β1)(β1,β1)βα2−(α2,β1)(β1,β1)β
对应两个向量的施密特法则
β1=α1β1=α1
β2=α2−(α2,β1)(β1,β1)β1β2=α2−(α2,β1)(β1,β1)β1
可见蓝色向量为β2β2与β1β1是垂直的
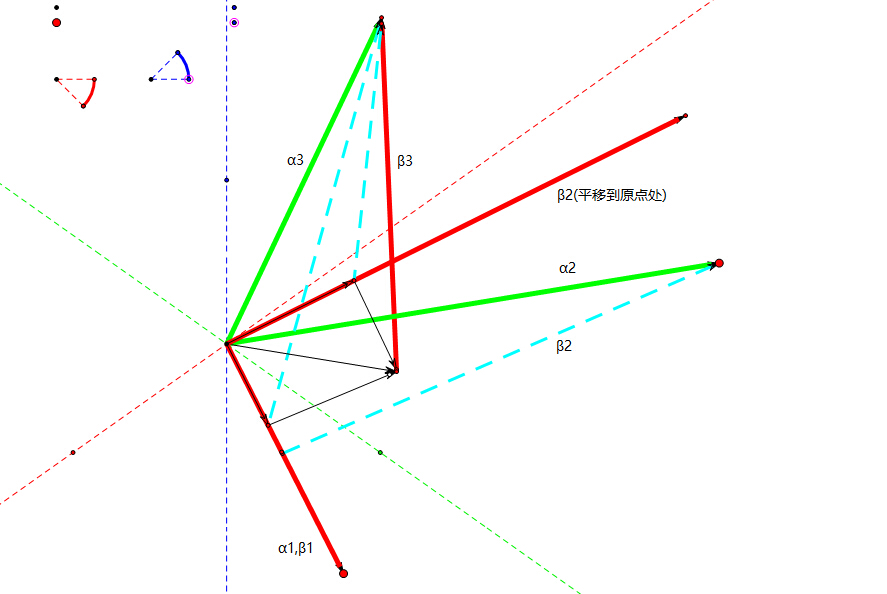
而当向量个数为3时,对应三维空间的几何解释如图
其中绿色的为需要正交的原始基αiαi(α1α1是红色的因为α1α1同时也是β1β1)
将二维得到的β2β2平移到坐标原点出后则α3α3在xoy平面的投影即是α3−(α3,β1)(β1,β1)β1−(α3,β2)(β2,β2)β2α3−(α3,β1)(β1,β1)β1−(α3,β2)(β2,β2)β2,即α3α3在β1β1和β2β2上的投影组成的平行四边形的斜边,则得到的β3β3就是α3α3与该投影的向量差,即红色部分的β3β3,显然可以看出来β1,β2,β3β1,β2,β3是正交的。
同样可以推广到三维以上的欧氏空间RmRm,即施密特正交公式。