周期信号的谐波与次谐波
振动信号中的谐波与次谐波
搜寻脉冲星候选体的时候,发现一个很像的候选体,首先排除了谐波信号(基波的1/n or n倍数);
询问pan老师后,得知还有m/n倍数关系的谐波!!翻遍网络似乎找到一个叫次谐波的概念,会出现m/n的倍数关系的周期。
1.次谐波分析
次谐波振动(又称亚谐波振动)是由于非线性系统的共振现象引起的。在现实中,振动系统基本都是非线性的,只有少数理想模型是线性的,比如我们所说的单摆模型。不同的非线性系统产生的次谐波频率也是不一样的,比如经典的Duffing系统,动力学系统如下所示。当激励频率接近系统固有频率的1/3时,产生1/3次谐波共振,这时频谱图上会出现固有频率及1/3倍固有频率。
当机械设备出现摩擦、松动、裂纹等故障时,常常会在低频中产生次谐波共振现象。在次谐波响应中,对称型的非线性振动产生奇次谐波响应;不对称型的非线性振动产生偶次谐波响应。摩擦、松动、裂纹等故障一般是不对称的非线性振动,因此多数情况下是产生转速频率的1/2次谐波响应,也有时候会出现1/4,3/2等频率成分,具体情况要结合对应的动力学模型进行分析。
次谐波没有谐波出现的频率高,只有在少数几种场景才可能发生。次谐波频率成分是比较难分析的,如果是人工分析,且提前根据转速计算出了设备特征频率,还是可以判断出次谐波频率的。如果是计算机软件分析就比较困难了,这种频率常常会被当作未知频率来处理,或者被当作某个一倍频来处理,这时候就会出现一些误判。
相应的过程如下:
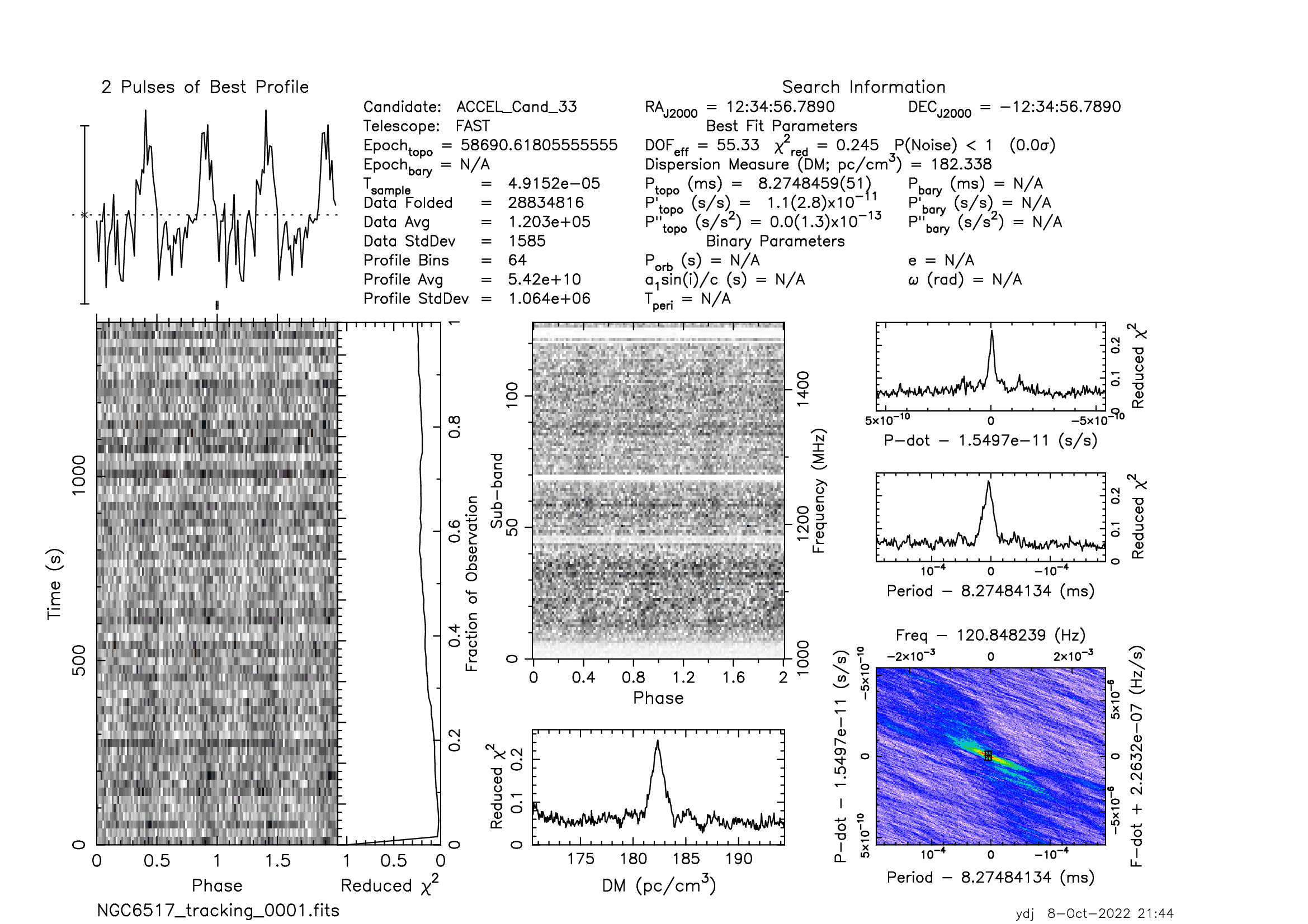
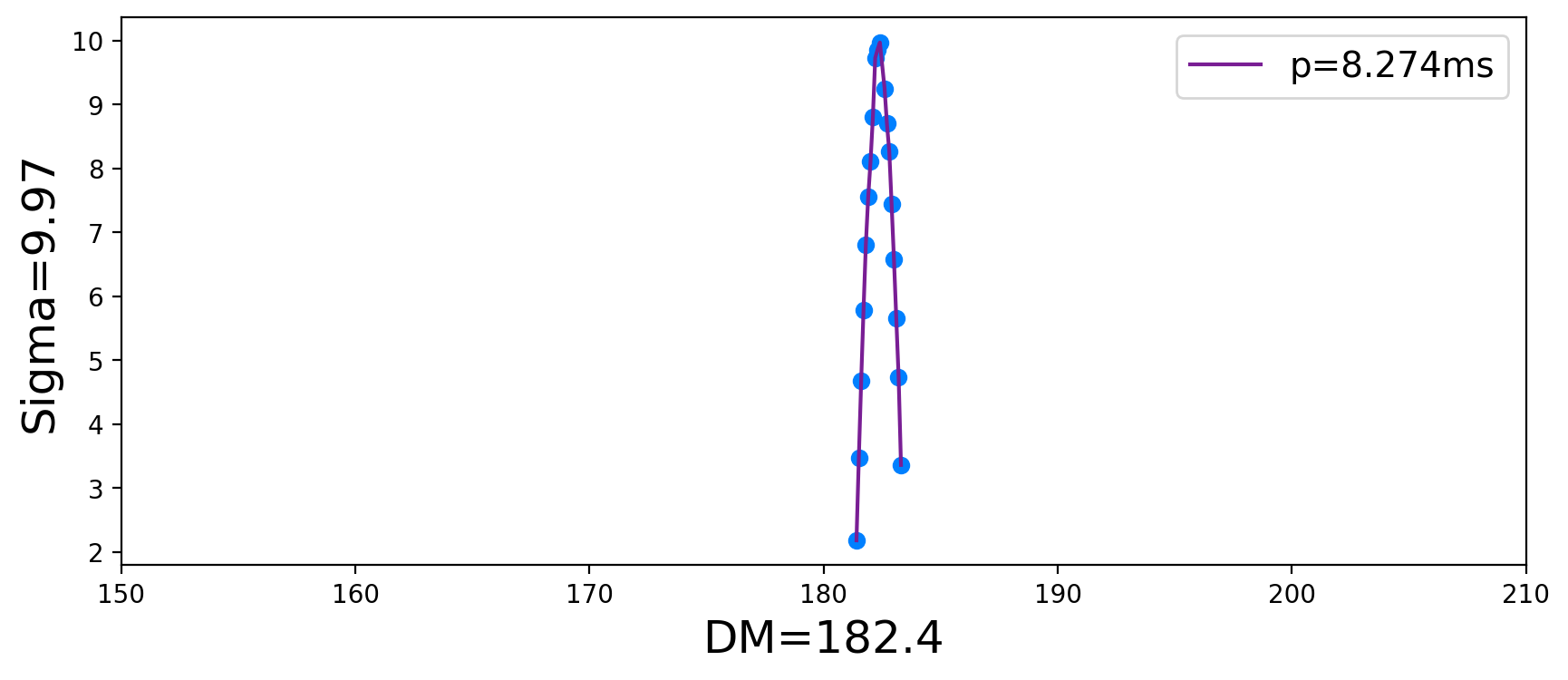
判断:
p = 8.27484 m = range(1,15,1) n = range(1,15,1) harm = [] for i in range(1,len(m)+1,1): for j in range(1,len(n)+1,1): harm.append(i/j) cand_p = [] for i in range(len(harm)): cand_p.append(harm[i]*p)
## p*3.5 = 28.96194 NGC6517B (p=28.96159 ms)
set(cand_p) ##去除重复
ref:



