最长回文子串

参考：力扣

关于回文串

"回文串”（palindromic string）是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串。

方式一：动态规划

由外而内，外层是否是回文字符串取决于首尾是否相等+内层是否是回文字符串  （内层字符长度大于1）

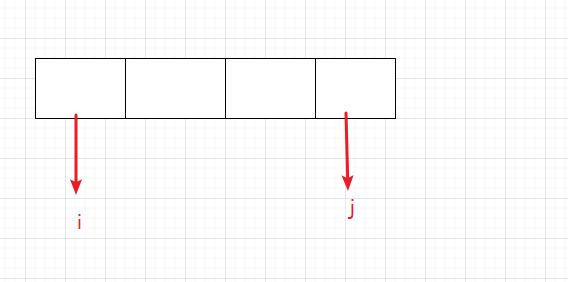
 i到j是否是回文串，由外而内的思路是：

取决于char[i] == char[j]?

　　再看i+ 1到j-1是否是回文串

 

转化成矩阵

i要小于j，因为i是头，j是尾  =》对角线右上半部分数据有效

 复杂度分析

两层关于规模n的for循环——时间复杂度为O(n^2)

二维数组，长宽均与n有关——空间复杂度O(n^2)

 /**
     * 动态规划
     * 回文字符串去掉首尾仍旧是回文字符串
     * 子串是回文字符串，首尾加上一样的字符，新串是回文字符串
     * dp[i][j]为true的条件：首尾相同，且子串长度为1或者子串是回文串
     * 此法只针对字符串长度大于1的，长度为1一定是回文子窜
     * dp[i,j]=true中，最大的j-i+1即最长回文字符串
     *
     * @param s
     * @return
     */
    public String dynamicPlaning(String s) {
//        传入字符串长度
        int length = s.length();
        if (length < 2) {
//            一个字符，恒成立
            return s;
        }
//        最长子串
        int maxlen = 1;
//        起始坐标0
        int begin = 0;
//      1.状态定义
//        dp[i,j]表示s[i...j]是否是回文子串

//        2.初始化  坐标矩阵
        boolean[][] dp = new boolean[length][length];
        for (int i = 0; i < length; i++) {
//            从i到i：单个字符——恒成立，设置其状态
            dp[i][i] = true;
        }
//        转换成字符数组填表
        char[] chars = s.toCharArray();
//        3.状态转移  重点，中心思想
//          先填左下角
//          先列再行，保证左下方的单元格先进行计算  数组长度>1，j从1开始
        for (int j = 1; j < length; j++) {
//            i要小于j:左边下标小于右边下标，相等的情况(对角线上)已经填写
            for (int i = 0; i < j; i++) {
//                判断首尾
//                    首尾不同 直接false
                if (chars[i] != chars[j]){
                    dp[i][j] = false;
                }else{
//                    首尾相等的情况下
//                      考虑去掉首尾之后，有两种情况
//                          只剩一个字符(j-1)-(i+1)+1<2 : j-i<3
                    if (j-i<3){
                        dp[i][j] = true;
                    }else{
//                        子串长度>1,取决于子串是否是回文字符串
                        dp[i][j] = dp[i+1][j-1];
                    }
                }
//                更新记录回文长度和起始位置 maxlen是前一个回文字符串的长度，如果该回文字符串>上一个回文字符串 maxlen被替换并记录初始下标
                if (dp[i][j]&&j-i+1>maxlen){
//                    记录此次回文字符串长度
                    maxlen=j-i+1;
//                    此次回文字符串初始下标
                    begin=i;
                }
            }
        }

//        4.返回值
//        substring(begin,end) 左闭右开 要截取的是begin到begin+maxlen-1 所以substring的end是begin+maxlen
        return s.substring(begin,begin+maxlen);
    }

 

test

    1         @Test
    2         public void tstDynamic(){
    3 //        随机产生字符串
    4 //        String s= RandomStringUtils.random(100,true,true);
    5 //        System.out.println(s);
    6 
    7 //        手动new字符串
    8                 String s="affasfasfasfdsgdfhtjghkhjdfghjjlasdfghjkllkjhgfdsa";
    9 //        asdfghjkllkjhgfdsa
   10                 System.out.println(solution.dynamicPlaning(s)+"长度："+solution.dynamicPlaning(s).length());
   11         }

 

方式二：中心扩散

由内而外，内层是回文字符串，判断外层是否也是的条件是扩散的新左右边界字符相同

遍历每个字符元素，判断每个字符能够扩散的最大长度，进行比较，取最大的就是整个字符串的最大回文子串

要分奇数偶数长度，奇数长度，中心轴是中间那个元素，偶数长度，中心轴是中间两个元素，轴对称的进行扩展

回文字符串肯定是轴对称的

 

 

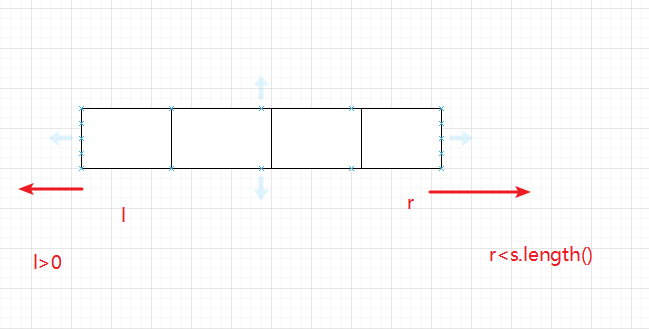
 右边：i+l/2和i+(l-1)/2  =》  取i+l/2

左边: i-(l-1)/2 和 i-(l-2)/2 => 取i-(l-1)/2

/**
 * @author 夜神
 * 以边界条件为中心，向外扩展，首尾相同则为回文，继续扩展，不同则不是回文，子串为最大回文
 */
public class CenterDispersal {
//    调用扩散逻辑，进行长度判断，并取得最长回文子串
    public String longestPalindrome(String s){
        if (s==null||s.length()<1) {
            return "";
        }
//        初始化最大回文子串的起点和终点
        int start = 0,end = 0;
//        遍历每个位置，当作中心 注意是每个位置，每个位置都作为中心一次，所以只需要一个for
        for (int i = 0;i < s.length(); i++){
//            分别拿到奇数偶数的回文子串长度
            int len1=expandAroundCenter(s,i,i);
//            偶串左右起始边界不是同一个，且必须要有两个才能轴对称
            int len2=expandAroundCenter(s,i,i+1);
//            对比最大长度
            int len = Math.max(len1,len2);
//            计算对应每一个最大回文子串的起点和终点
            if (len>end-start){
//                无论奇数偶数都一样 这里是综合里奇偶两种情况的结果
                start= i-(len-1)/2;
                end=i+len/2;
            }
        }
//        substring函数左闭右开
        return s.substring(start,end+1);
    }

    /**
     *扩散逻辑
     * @param s 输入的字符串
     * @param left 起始的左边界
     * @param right 起始的有边界
     * @return 回文串的 长度
     */
    private int expandAroundCenter(String s,int left,int right){
//        left=right的时候，回文中心是一个字符，回文串长度是奇数
//        right=left+1的时候，回文中心是一个空隙，回文串长度是偶数

        int l=left,r=right;
//        从中心向两边扩散，l--不能<0,L大于0，右边小于长度,且首尾相等，满足条件就继续扩散
//        跳出循环的时候恰好满足s.charAt(left) != s.charAt(right)，其去掉首尾的子串为最大子回文串
        while (l>0&&r<s.length()&&s.charAt(l)==s.charAt(r)){
            l--;
            r++;
        }
//        最大回文串长度——跳出时字符串子串长度
        return r-l-1;
    }
}

 

 

test

/**
 * 字符串中找最大回文子串
 * @author 夜神
 */
public class TestSolution {
    private DynamicPlan solution=new DynamicPlan();
    private CenterDispersal centerDispersal=new CenterDispersal();
    @Test
    public void tstDynamic(){
//        随机产生字符串
//        String s= RandomStringUtils.random(100,true,true);
//        System.out.println(s);

//        手动new字符串
        String s="affasfasfasfdsgdfhtjghkhjdfghjjlasdfghjkllkjhgfdsa";
//        asdfghjkllkjhgfdsa
        System.out.println(solution.dynamicPlaning(s)+"长度："+solution.dynamicPlaning(s).length());
    }

    @Test
    public void testCenterDispersal(){
        String s="affasfasfasfdsgdfhtjghkhjdfghjjlasdfghjkllkjhgfdsa";
        String longestPalindrome = centerDispersal.longestPalindrome(s);
        System.out.println(longestPalindrome+", length:"+longestPalindrome.length());
    }

}