NOIP2022 T1 种花 题解
Part 1 吐槽&退役寄
考场上唯一AC的题目，T3看错题以为可以删去不止1条边，T4输出没换行，寄。
最后喜提100+0+0+0，给我的OI生涯画上了一个不完美的句号。
Part 2 题解
题目让统计C和F的数量。
先来考虑较简单的C的情况。
不妨记C左边的一列为C的“一竖”
可以发现：
如果固定C左边的“一竖”的话，那么此时C的“上底”和“下底”所在的行是确定的，如图：
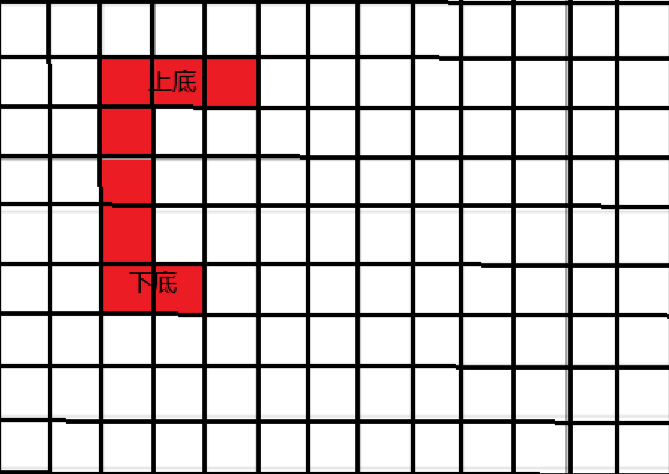
那么怎么统计数量？
不妨记\(r_{i,j}\)表示从\((i,j)\)这个点出发，向右最远能到的是土坑的格子的列数。
可以发现，两个有着相同的“一竖”的C是不同的，当且仅当上底不同，或者下底不同。
设”一竖“所在的列数为\(i\)，上底的行数为\(p1\)，下底的行数为\(p2\)，于是有乘法原理：\(cnt=(r_{p1,i}-i)(r_{p1,i}-i)\)
于是考虑\(O(n^2)\)预处理数组\(r\)，\(O(n^3)\)枚举左边的“一竖”，对于每个一竖暴力统计即可。
看到\(n\leq1000\)，考虑优化成\(n^2\)。
记当前枚举的左边的“一竖”的上端点为\((i,j)\)，那么以\(i\)为行数的“上底”能造成多少贡献呢？
可以发现：
\(ANS=(r_{i,j}-j)\sum\limits_{i+2\leq k\leq d_{i,j}} (r_{k,j}-j)\)
其中\(d\)数组是从位置\((i,j)\)向下能到达的最下面的是土坑位置的行数。
于是自然而然地想到了可以用前缀和优化，也就是在\(O(n^2)\)的复杂度下预处理出从某个点最上面的不是土坑的点到这个位置的贡献和。注意，中间可能有土坑，前缀和数组可能是这样的：
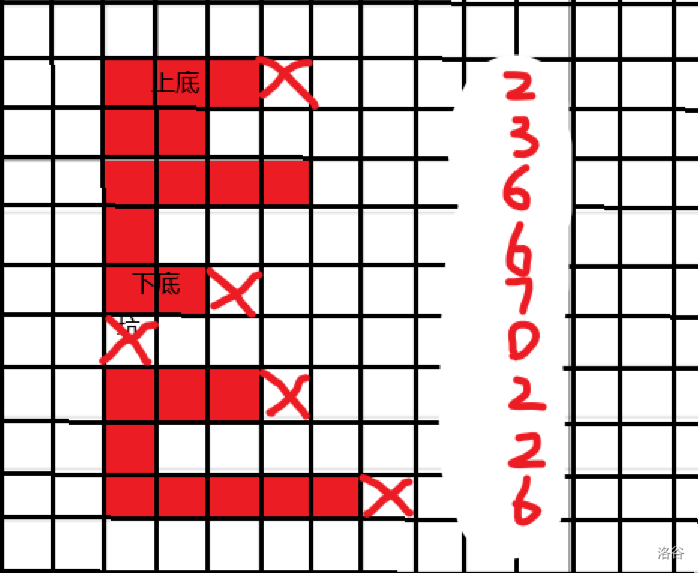
于是每枚举到一个C的上底的左顶点时，这个点的贡献可以整理成这样：
\(ANS=(r_{i,j}-j)\sum\limits_{i+2\leq k\leq d_{i,j}} (r_{k,j}-j)=(r_{i,j}-j)(SUM_{d_{i,j},j}-SUM_{i+1,j})\)
至此，完美解决C的情况。
那么F和C有什么练习与区别呢？
仔细观察发现，F是由上面的一个“C”和下面的一个小竖组成的。如果解决的C的情况，F自然也就迎刃而解了，只需要在前缀和中再乘以一个向下有多少长度即可，也就是
\(SUM'_{i,j}=SUM'_{i-1,j}+(r_{i,j}-j)(d_{i,j}-i)\)
于是本题全部解决。
Part 3 小细节
-
取模的时候要注意，不然有可能爆int
-
注意乘以题目所给的系数
-
最重要的一点！！！多测不清空，爆零两行泪
Part 4 考场上的代码
#include<bits/stdc++.h>
#define ll long long
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define req(i, a, b) for(int i = a; i >= b; i--)
#define MOD 998244353
#define mp make_pair
#define fir first
#define sec second
#define SIZE 1005
using namespace std;
int T, id;
char a[SIZE][SIZE];
ll r[SIZE][SIZE], d[SIZE][SIZE];
ll sum1[SIZE][SIZE], sum2[SIZE][SIZE];
int main(){
scanf("%d%d",&T, &id);
while(T--){
int n, m, c, f;
scanf("%d%d%d%d",&n, &m, &c, &f);
rep(i, 0, n + 1) rep(j, 0, m + 1) r[i][j] = d[i][j] = sum1[i][j] = sum2[i][j] = 0;
rep(i, 1, n){
rep(j, 1, m) cin >> a[i][j];
}
rep(i, 1, n){
req(j, m, 1){
if(a[i][j] == '1'){
r[i][j] = 0;
continue;
}
if(r[i][j + 1] == 0) r[i][j] = j;
else r[i][j] = r[i][j + 1];
}
}
rep(j, 1, m){
req(i, n, 1){
if(a[i][j] == '1'){
d[i][j] = 0;
continue;
}
if(d[i + 1][j] == 0) d[i][j] = i;
else d[i][j] = d[i + 1][j];
}
}
rep(j, 1, m){
rep(i, 1, n){
if(a[i][j] == '1') sum1[j][i] = sum2[j][i] = 0;
else {
sum1[j][i] = (sum1[j][i - 1] + r[i][j] - j) % MOD;
sum2[j][i] = (sum2[j][i - 1] + (r[i][j] - j) * (d[i][j] - i) % MOD) % MOD;
}
}
}
ll ans1 = 0, ans2 = 0;
rep(i, 1, n){
rep(j, 1, m - 1){
if(i + 2 > d[i][j]) continue;
if(a[i][j] != '1') ans1 = (ans1 + (sum1[j][d[i][j]] - sum1[j][i + 1]) * (r[i][j] - j) % MOD) % MOD;
if(a[i][j] != '1') ans2 = (ans2 + (sum2[j][d[i][j]] - sum2[j][i + 1]) * (r[i][j] - j) % MOD) % MOD;
}
}
printf("%lld %lld\n",ans1 * c, ans2 * f);
}
return 0;
}
Part 5 祝愿
希望各位能在OI的道路上越走越远，不留遗憾！——已经AFO的蒟蒻。
