算法第五章作业

1. 题目——最小重量机器设计问题

设某一机器由n个部件组成，每一种部件都可以从m个不同的供应商处购得。设Wij是从供应商j处购得的部件i的重量，Cij是相应的价格。试设计一个算法，给出总价格不超过d的最小重量机器设计。

 

 参考代码：

#include <iostream>
using namespace std;

int n;
int m;
int d;
int w[100][100];
int c[100][100];
int x[100];
int minx[100];
int minw = 10000000;
int curw = 0;
int curc = 0;

void backtrack (int t) {
    if (t > n) {
        if (minw > curw && curc <= d) {
            minw = curw;
            for (int i = 1; i <= n; i++) {
                minx[i] = x[i];
            }
        }
        return;
    } else {
        for (int i = 1; i <= m; i++) {
            if (curc + c[t][i] <= d && curw + w[t][i] < minw) {
                x[t] = i;
                curw += w[t][i];
                curc += c[t][i];
                backtrack(t+1);
                curw -= w[t][i];
                curc -= c[t][i];
            }
            
        }
    }
}

int main() {
    cin >> n >> m >> d;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> c[i][j];
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> w[i][j];
        }
    }
    backtrack(1);
    cout << minw << endl;
    for (int i = 1; i <= n; i++) {
        cout << minx[i] << " ";
    }
    return 0;
}

2. 回溯法分析“最小重量机器设计问题”

2.1 说明“最小重量机器设计问题”的解空间

解空间即进行穷举的搜索空间，包含所有的可能解，这里以样例为例写出解空间：

（1，1，1）（1，1，2）（1，1，3）

（1，2，1）（1，2，2）（1，2，3）

（1，3，1）（1，3，2）（1，3，3）

（2，1，1）（2，1，2）（2，1，3）

（2，2，1）（2，2，2）（2，2，3）

（2，3，1）（2，3，2）（2，3，3）

（3，1，1）（3，1，2）（3，1，3）

（3，2，1）（3，2，2）（3，2，3）

（3，3，1）（3，3，2）（3，3，3）

说明：（1，1，1）表示第1个部件选择第1个供应商，第2个部件选择第1个供应商，第3个部件选择第1个供应商，以此类推。

2.2 说明“最小重量机器设计问题”的解空间树

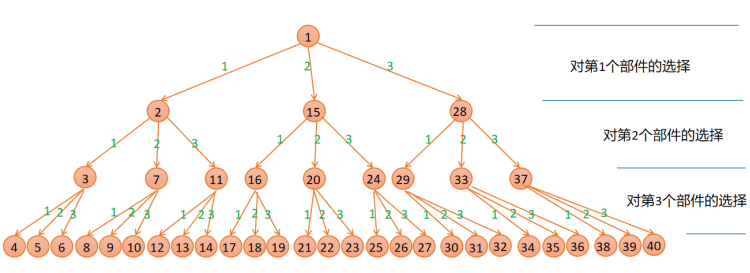
2.3 在遍历解空间树的过程中，每个结点的状态值

每个结点的状态值包括：该结点的重量w、该结点的价格。

3. 对回溯法的理解

（1）基本思想：构建问题的解空间树，在其解空间树中，从根节点出发，进行深度优先搜索。在搜索过程中，对解空间树的每个结点进行判断，判断该结点是否包含问题的解，若肯定不包含，则跳过对以该结点为根的子树的搜索，逐层向其祖先结点回溯。否则，则进入该子树，继续按深度优先策略搜索。

（2）步骤：①针对所给问题，定义其解空间；

②确定易于搜索的解空间结构；

③深度优先搜索其解空间，并在搜索过程中用剪枝函数避免无效搜索。

（3）剪枝：回溯法搜索空间树时，常用限界函数和约束函数避免无效搜索，其中约束函数将不满足约束的子树剪去，限界函数将得不到最优解的子树。一般可以利用这两种剪枝方式提升算法的效率，避免大量的不必要搜索。