从方向导数到梯度：深度学习中的关键数学概念详解

• 方向导数作为标量量，表征了函数在特定方向上的变化率。其数学表示为 ∇ᵤf(x) 或 Dᵤf(x)。
• 对于标量函数 f(x): Rⁿ → R，其梯度由函数的偏导数构成向量场。梯度向量指向函数值增长最快的方向，其模长等于该方向的方向导数。
• 方向导数的计算可通过两种方法实现：其一是引入函数 g(s) = f(x + su)，方向导数即为 g′(0)；其二是利用方向导数等于梯度与方向向量点积的性质：∇ᵤf(x) = ∇f(x)u。

引论

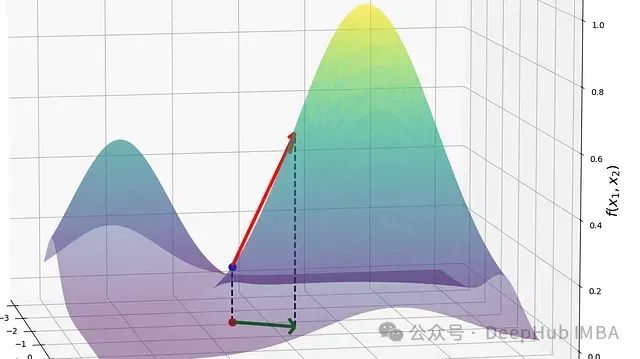
函数在不同方向上的变化特性分析在诸多领域具有重要意义，典型应用如神经网络中利用梯度更新权重的训练过程。本文将系统探讨方向导数与梯度的理论基础，并通过如下等式阐述二者的内在联系：

 

https://avoid.overfit.cn/post/7bd19d5225cf4f908139e0178ae7d901