贝叶斯统计中常见先验分布选择方法总结

在贝叶斯统计中,选择合适的先验分布是一个关键步骤。本文将详细介绍三种主要的先验分布选择方法:

1. 经验贝叶斯方法
2. 信息先验
3. 无信息/弱信息先验

经验贝叶斯方法

经验贝叶斯方法是一种最大似然估计(MLE)方法,通过最大化先验分布下数据的边际似然来估计先验分布的参数。设X表示数据,θ表示参数,则经验贝叶斯估计可表示为:

θ = argmax P(X|θ)

信息先验

信息先验是一种基于先前知识或以前研究结果,纳入了关于估计参数信息或信念的先验分布。信息先验有以下几个关键特点:

1. 在样本量小或数据有噪声的情况下,信息先验可以导致更有效和准确的推断。
2. 通过对先验信息赋予更大的权重,信息先验可以帮助正则化估计并避免过拟合。
3. 信息先验有助于将特定领域的知识或假设纳入模型,例如对参数值的约束或参数之间的关系。

以下是一些常见的信息先验及其特点:

1. Beta先验

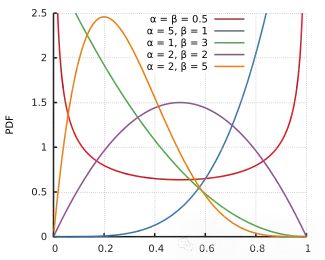
Beta先验的概率密度函数(PDF)由下式给出:

https://avoid.overfit.cn/post/afca60c17dc84efaaef87ef88565c838