号称能打败MLP的KAN到底行不行？数学核心原理全面解析

前几天火爆的Kolmogorov-Arnold Networks是具有开创性，目前整个人工智能社区都只关注一件事LLM。我们很少看到有挑战人工智能基本原理的论文了，但这篇论文给了我们新的方向。

mlp或多层感知位于AI架构的最底部，几乎是每个深度学习架构的一部分。而KAN直接挑战了这一基础，并且也挑战了这些模型的黑箱性质。

也许你看到了很多关于KAN的报告，但是里面只是简单的描述性介绍，对于他的运行原理还是不清楚，所以我们这篇文章将涉及大量的数学知识，主要介绍KAN背后的数学原理。

KAN

Kolmogorov-Arnold Networks引入了一种基于Kolmogorov-Arnold表示定理的新型神经网络架构，为传统的多层感知器(mlp)提供了一种有前途的替代方案。

mlp在节点(“神经元”)上有固定的激活函数，而kan在边缘(“权重”)上有可学习的激活函数。kan根本没有线性权重，每个权重参数都被参数化为样条的单变量函数。这个看似简单的改变使得KANs在准确性和可解释性方面优于mlp。KANs是mlp的有希望的替代品，为进一步改进当今严重依赖mlp的深度学习模型提供了机会。

上面论文的原文，根据论文在数据拟合和PDE求解方面，更小的kan与更大的mlp相当或更好。所以kan可能比mlp拥有更快的神经缩放定律。并且KANs可以直观地可视化，大大提高了可解释性。

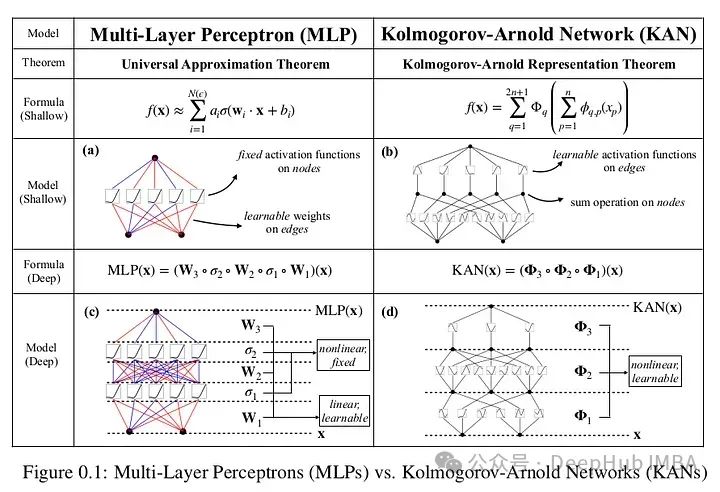
论文围绕函数逼近的Kolmogorov-Arnold表示定理的性质展开，这是这篇论文的全部前提。

表示定理基础:函数被分解成更简单的函数，然后使用神经网络进行近似。

平滑性和连续性:目标是确保原始多元函数的平滑性有效地转化为神经网络近似。

空间填充曲线:函数跨维度的属性，特别是关注在近似过程中如何保持连续性和其他函数属性或转换。

 

https://avoid.overfit.cn/post/6ee2307e614b462f9c9aac26ef12252d