奇异值分解（SVD）和图像压缩

在本文中，我将尝试解释 SVD 背后的数学及其几何意义，还有它在数据科学中的最常见的用法，图像压缩。

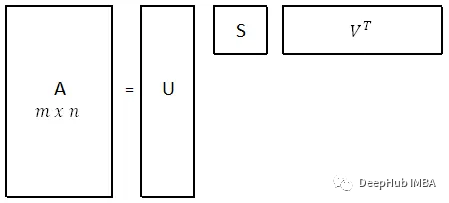
奇异值分解是一种常见的线性代数技术，可以将任意形状的矩阵分解成三个部分的乘积：U、S、V。原矩阵A可以表示为：

具体来说，A矩阵中的奇异值就是\Sigma矩阵中的对角线元素，它们是矩阵A的特征值的平方根，表示A矩阵在各个主方向上的拉伸程度。U矩阵是AA^T的特征向量构成的正交矩阵，表示数据集在降维后的新的坐标系中的投影。V矩阵是A^TA的特征向量构成的正交矩阵，表示每个数据点在降维后的新坐标系中的坐标。

 

完整文章：

https://avoid.overfit.cn/post/f0a675aad6994b61a2aa93fb647a0633