基于凸集上投影（POCS）的聚类算法

POCS：Projections onto Convex Sets。在数学中，凸集是指其中任意两点间的线段均在该集合内的集合。而投影则是将某个点映射到另一个空间中的某个子空间上的操作。给定一个凸集合和一个点，可以通过找到该点在该凸集合上的投影来进行操作。该投影是离该点最近的凸集内的点，可以通过最小化该点和凸集内任何其他点之间的距离来计算。既然是投影，那么我们就可以将特征映射到另一个空间中的凸集合上，这样就可以进行聚类或降维等操作。

本文综述了一种基于凸集投影法的聚类算法，即基于POCS的聚类算法。原始论文发布在IWIS2022上。

凸集

凸集定义为一个数据点集合，其中连接集合中任意两点x1和x2的线段完全包含在这个集合中。根据凸集的定义，认为空集∅、单集、线段、超平面、欧氏球都被认为是凸集。数据点也被认为是凸集，因为它是单例集（只有一个元素的集合）。这为 POCS 的概念应用于聚类数据点开辟了一条新路径。

凸集投影(POCS)

POCS方法大致可分为交替式和并行式两种。

1、交替式poc

从数据空间中的任意一点开始，从该点到两个(或多个)相交凸集的交替投影将收敛到集合交点内的一点，例如下图：

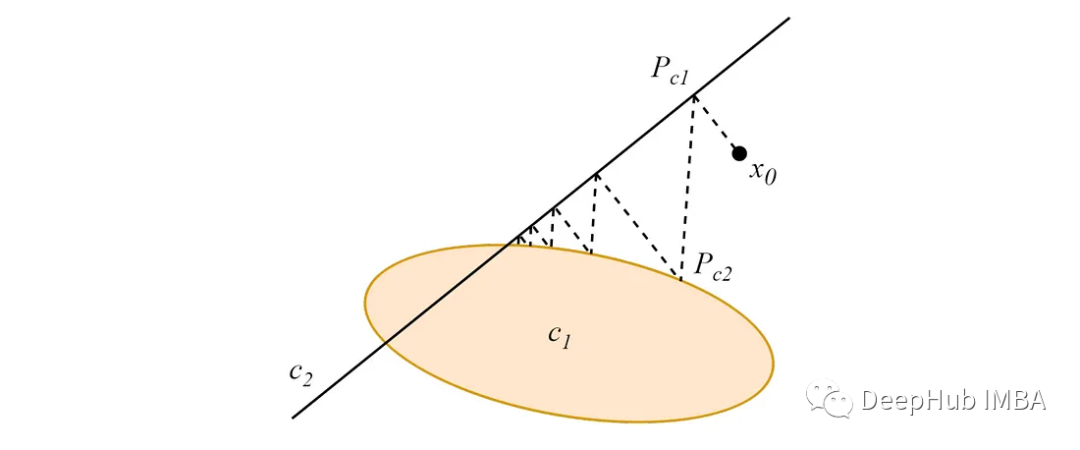
当凸集不相交时，交替投影将收敛到依赖于投影阶数的greedy limit cycles。

 

https://avoid.overfit.cn/post/bd811302f89c47fa8777c9f5bac8c59e