[SDOI2015][bzoj3994] 约数个数和 [莫比乌斯反演]

题面：

传送门

思路：

首先，我们需要证明一个结论：d(i*j)等于sigma(gcd(x,y)==1)，其中x为i的约数，y为j的约数

对于nm的每一个质因子pi分别考虑，设n = pi^ai + n'，m = pi^bi + m'

那么显然质因子pi对d(nm)的贡献为(ai+bi+1)

同理，考虑右边的式子，我们发现质数pi对右侧做的贡献仍然是(ai+bi+1)，即如下的(x,y)

(pi^ai,1) (pi^(ai-1),1) ..... (1,1) .....(1,pi^(bi-1)) (1,pi^bi)

因此左右两式相同

因此原待求表达式化为如下形式：

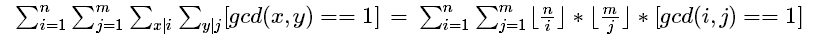
由莫比乌斯函数第二情况得：上式可化为

其中g(i)表示前半个式子中的那段东西，相当于d(i)的前缀和

于是O(Tsqrt(min(n,m))轻松解决

顺便说一句，求约数个数也有线性的方法

记录c[i]表示i的最小的质因子的次数

每次更新这个，然后同时用c[i]+1更新d[i*pri[j]]即可

 

Code：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
inline ll read(){
    ll re=0,flag=1;char ch=getchar();
    while(ch>'9'||ch<'0'){
        if(ch=='-') flag=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9') re=(re<<1)+(re<<3)+ch-'0',ch=getchar();
    return re*flag;
}
ll mu[100010],pri[100010],c[100010],d[100010],cnt;bool vis[100010];
void init(ll n){
    mu[1]=d[1]=c[1]=1;ll i,j,k;
    for(i=2;i<=n;i++){
        if(!vis[i]){
            pri[++cnt]=i;mu[i]=-1;c[i]=1;d[i]=2;
        }
        for(j=1;(j<=cnt)&&(i*pri[j]<=n);j++){
            k=i*pri[j];vis[k]=1;
            if(i%pri[j]==0){
                d[k]=d[i]/(c[i]+1)*(c[i]+2);
                c[k]=c[i]+1;break;
            }
            mu[k]=-mu[i];
            d[k]=d[i]*d[pri[j]];c[k]=1;
        }
    }
    for(i=1;i<=n;i++) mu[i]+=mu[i-1];
    for(i=1;i<=n;i++) d[i]+=d[i-1];
}
ll n,m;
int main(){
    ll i,j,T=read(),ans;init(50000);
    while(T--){
        n=read();m=read();ans=0;
        if(n>m) swap(m,n);
        for(i=1;i<=n;i=j+1){
            j=min(n/(n/i),m/(m/i));
            ans+=(mu[j]-mu[i-1])*d[n/i]*d[m/i];
        }
        printf("%lld\n",ans);
    }
}