[HNOI2007][BZOJ1185] 最小矩形覆盖 [凸包+旋转卡壳]
题面
前置芝士
建议先学习向量相关的计算几何基础
计算几何基础戳这里
思路
用这道题学习一下凸包和旋转卡壳
首先是凸包部分
凸包
求凸包用的算法是graham算法
算法流程如下:
找到$y$坐标最小的一点作为原点
对原点之外的所有点按照到原点的极角排序(这里因为选取了最靠下的,所以极角范围在$[0,\pi]$)
依次遍历所有排序后的点,加入一个单调栈中:每次判断(栈顶元素和栈顶第二元素之间的斜率)是否大于(当前点和栈顶第二元素之间的斜率)
注意一旦这个大于成立了,栈顶元素就会在当前元素和栈顶第二元素的连线的“下面”,也就是在凸包里面了
因为我们事先按照极角排序了,所以这一单调栈可以不重复不遗漏地记录凸包上所有点
注意这样求出来的凸包上的点是逆时针排序的(根本原因是因为极角排序就是逆时针绕圈)
graham算法的复杂度是$O(n\log n)$,瓶颈是排序
旋转卡壳
首先,我在这道题里面用的不是标准的旋转卡壳算法......但是也是“旋转+卡壳”的思路
标准版的旋转卡壳戳这里,这里标准版指的是用4条边去卡壳,我写的是一条边和3个极值点
对于最小面积矩形,我们有结论:这一外接矩形一定有一条边和凸包的一条边重合
注意这个结论对于最小周长矩形依然成立
证明嘛......我愣是没找到。感性理解一下就是对于一个四边都接在凸包端点上的矩形,把它旋转一下一定更优
核心算法流程如下:
我们遍历凸包上的每一条边,并对于每一条边求出以这条边为x轴时,最靠左的点、最靠右的点、最靠上的点
设求出来的凸包上的点是$q[0...m-1]$
假设我们当前的边的两个端点是凸包上的$q[i],q[i+1]$,而且是有向的(i指向i+1),那么上述三个端点有如下性质:
对于最靠左的点$q[l]$,$vec(q[i],q[l])\ast vec(q[i],q[i+1])$是所有$l$中最小的
对于最靠右的点$q[r]$,$vec(q[i],q[r])\ast vec(q[i],q[i+1])$是所有$r$中最大的
对于最靠上的点$q[u]$,$vec(q[i],q[i+1])$叉乘$vec(q[i],q[u])$是所有$u$中最大的
其中$vec(u,v)$表示从点$u$指向$v$的向量
前两个的证明,利用点乘的性质:因为点乘的被投影向量长度相等,所以决定点乘结果大小的就是投影的大小
那么显然投影最小最靠左,投影最大最靠右
第三个的证明,利用叉乘的性质:叉乘等于两个向量逆时针旋转构成的有向平行四边形面积
因为平行四边形底边长度相同,而且$vec(q[i],q[i+1])$一定在所有从$q[i]$出发的向量的顺时针方向,所以反过来旋转一定是正的,叉乘最大就是最高
图示如下:
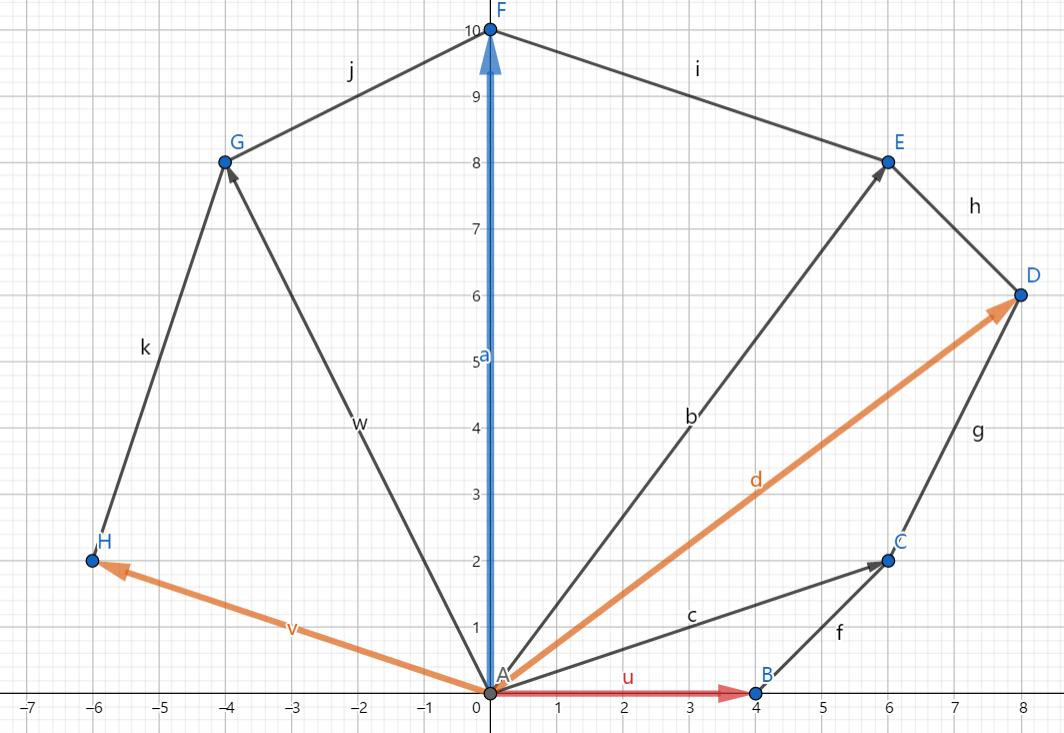
知道了这三个点以后,我们就可以知道这个矩形的长宽,进而求出面积了
又有性质:我们每次从$vec(q[i],q[i+1])$旋转到$vec(q[i+1],q[i+2])$的时候,$l,r,u$也会跟着逆时针旋转,所以只要枚举即可
这样,整个旋转卡壳就是“遍历所有边”+“顺序求出端点”的过程,总复杂度是$O(n)$的
Code
代码中node是向量结构体,对于点我们用位矢表示,也是向量
标$\ast$的是叉乘,标\的是点乘
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cassert>
#include<cmath>
#define eps 1e-9
#define ll long long
using namespace std;
inline int read(){
int re=0,flag=1;char ch=getchar();
while(!isdigit(ch)){
if(ch=='-') flag=-1;
ch=getchar();
}
while(isdigit(ch)) re=(re<<1)+(re<<3)+ch-'0',ch=getchar();
return re*flag;
}
struct node{
double x,y;
node(double xx=0.0,double yy=0.0){x=xx;y=yy;}
inline bool operator <(const node &b){return ((fabs(y-b.y)<eps)?(x<b.x):(y<b.y));}
inline friend bool operator ==(const node &a,const node &b){return ((fabs(a.x-b.x)<eps)&&(fabs(a.y-b.y)<eps));}
inline friend bool operator !=(const node &a,const node &b){return !(a==b);}
inline friend node operator +(const node &l,const node &r){return node(l.x+r.x,l.y+r.y);}
inline friend node operator -(const node &l,const node &r){return node(l.x-r.x,l.y-r.y);}
inline friend node operator *(node l,double r){return node(l.x*r,l.y*r);}
inline friend double operator *(const node &l,const node &r){return l.x*r.y-l.y*r.x;}
inline friend double operator /(const node &l,const node &r){return l.x*r.x+l.y*r.y;}
inline friend double dis(const node &a){return sqrt(a.x*a.x+a.y*a.y);}
}a[100010],q[100010],x[10];
int n,top;double ans=1e60;
inline bool cmp(node l,node r){
double tmp=(a[1]-l)*(a[1]-r);
if(fabs(tmp)<eps) return dis(a[1]-l)<dis(a[1]-r);
else return tmp>0;
}
void graham(){//get a counter-clockwise convex
int i;
for(i=2;i<=n;i++){
if(a[i]<a[1]) swap(a[1],a[i]);
}
sort(a+2,a+n+1,cmp);
q[++top]=a[1];
q[++top]=a[2];
for(i=3;i<=n;i++){
while(top>1&&((q[top]-q[top-1])*(a[i]-q[top])<eps)) top--;
q[++top]=a[i];
}
q[0]=q[top];
}
void RC(){//RotatingCalipers
int l=1,r=1,p=1,i;
double L,R,D,H,tmp;
for(i=0;i<top;i++){
D=dis(q[i]-q[i+1]);
while((q[i+1]-q[i])*(q[p+1]-q[i])-(q[i+1]-q[i])*(q[p]-q[i])>-eps) p=(p+1)%top;
while((q[i+1]-q[i])/(q[r+1]-q[i])-(q[i+1]-q[i])/(q[r]-q[i])>-eps) r=(r+1)%top;
if(i==0) l=r;
while((q[i+1]-q[i])/(q[l+1]-q[i])-(q[i+1]-q[i])/(q[l]-q[i])<eps) l=(l+1)%top;
L=(q[i+1]-q[i])/(q[l]-q[i])/D;
R=(q[i+1]-q[i])/(q[r]-q[i])/D;
H=(q[i+1]-q[i])*(q[p]-q[i])/D;
tmp=(R-L)*H;
if(tmp<ans){
ans=tmp;
x[0]=q[i]+(q[i+1]-q[i])*(R/D);
x[1]=x[0]+(q[r]-x[0])*(H/dis(x[0]-q[r]));
x[2]=x[1]-(x[0]-q[i])*((R-L)/dis(q[i]-x[0]));
x[3]=x[2]-(x[1]-x[0]);
}
}
}
int main(){
n=read();int i,j;
for(i=1;i<=n;i++) scanf("%lf%lf",&a[i].x,&a[i].y);
graham();
RC();
printf("%.5lf\n",ans);
j=0;
for(i=1;i<4;i++) if(x[i]<x[j]) j=i;
for(i=0;i<4;i++) printf("%.5lf %.5lf\n",x[j].x,x[j].y),j=(j+1)%4;
}
