DFS(二）

 

117. 填充每个节点的下一个右侧节点指针 II

难度中等

给定一个二叉树

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

 

进阶：

  • 你只能使用常量级额外空间。
  • 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

 

示例：

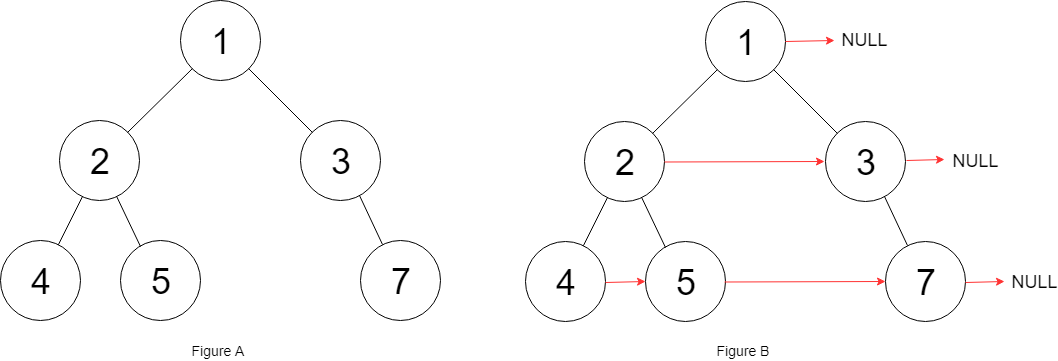
　输入：root = [1,2,3,4,5,null,7]

输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

 

提示：

  • 树中的节点数小于 6000
  • -100 <= node.val <= 100

 

 1 """
 2 # Definition for a Node.
 3 class Node:
 4     def __init__(self, val, left, right, next):
 5         self.val = val
 6         self.left = left
 7         self.right = right
 8         self.next = next
 9 """
10 class Solution:
11     def connect(self, root: 'Node') -> 'Node':
12         if root is None:
13             return None
14         if root.left:
15             if root.right:
16                 root.left.next = root.right
17             else:
18                 root.left.next = self.__nextLeftNode(root.next)
19         if root.right:
20             root.right.next = self.__nextLeftNode(root.next)
21         self.connect(root.right)
22         self.connect(root.left)
23         return root
24              
25     def __nextLeftNode(self, root: 'Node') -> 'Node':
26         while root:
27             if root.left:
28                 return root.left
29             elif root.right:
30                 return root.right
31             else:
32                 root = root.next
33         return None
View Code

129. 求根到叶子节点数字之和

难度中等

给定一个二叉树，它的每个结点都存放一个 0-9 的数字，每条从根到叶子节点的路径都代表一个数字。

例如，从根到叶子节点路径 1->2->3 代表数字 123。

计算从根到叶子节点生成的所有数字之和。

说明: 叶子节点是指没有子节点的节点。

示例 1:

输入: [1,2,3]
    1
   / \
  2   3
输出: 25
解释:
从根到叶子节点路径 1->2 代表数字 12.
从根到叶子节点路径 1->3 代表数字 13.
因此，数字总和 = 12 + 13 = 25.

示例 2:

输入: [4,9,0,5,1]
    4
   / \
  9   0
 / \
5   1
输出: 1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495.
从根到叶子节点路径 4->9->1 代表数字 491.
从根到叶子节点路径 4->0 代表数字 40.
因此，数字总和 = 495 + 491 + 40 = 1026.
 1 # Definition for a binary tree node.
 2 # class TreeNode:
 3 #     def __init__(self, x):
 4 #         self.val = x
 5 #         self.left = None
 6 #         self.right = None
 7 
 8 class Solution:
 9     def sumNumbers(self, root: TreeNode) -> int:
10         res = list()
11         self.__getNumbers(root, list(), res)
12         Sum = self.__computeNumbersSum(res)
13         return Sum
14     
15     def __getNumbers(self, root: TreeNode, path, res) -> None:
16         if not root:
17             return 
18         path = path + [root.val] 
19         if not root.left and not root.right:
20             res.append(path)
21             return
22         self.__getNumbers(root.left, path, res)
23         self.__getNumbers(root.right, path, res)
24         
25     def __computeNumbersSum(self, numbers):
26         Sum = 0
27         for eachElement in numbers:
28             Sum = Sum  + int( "".join([str(i) for i in eachElement]))
29         return Sum
View Code

130. 被围绕的区域

难度中等

给定一个二维的矩阵，包含 'X' 和 'O'（字母 O）。

找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例:

X X X X
X O O X
X X O X
X O X X

运行你的函数后，矩阵变为：

X X X X
X X X X
X X X X
X O X X

解释:

被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。

如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

 1 class Solution:
 2     def solve(self, board: List[List[str]]) -> None:
 3         """
 4         Do not return anything, modify board in-place instead.
 5         """
 6         if not board:
 7             return  
 8         row_num = len(board)
 9         column_num = len(board[0])
10     
11         self.__dfs(row_num, column_num, board)
12         self.__replace(row_num, column_num, board)
13 
14     def __dfs(self, row_num: int, column_num: int, board: List[List[str]])->None:  
15         if not board:
16             return
17         for index in range(row_num):
18             self.__dfsPre(index, 0, row_num, column_num, board)
19             self.__dfsPre(index, column_num-1, row_num, column_num, board)
20         for index in range(column_num):
21             self.__dfsPre(0, index, row_num, column_num, board)
22             self.__dfsPre(row_num-1, index, row_num, column_num, board)
23         
24     def __dfsPre(self, i_index: int, j_index: int, row_num: int, column_num: int, board: List[List[str]])->None:
25         
26         if i_index < 0 or i_index >= row_num \
27             or j_index < 0 or j_index >= column_num \
28             or board[i_index][j_index] != 'O':
29             return
30         board[i_index][j_index] = 'B'
31         self.__dfsPre(i_index-1, j_index, row_num, column_num, board)
32         self.__dfsPre(i_index+1, j_index, row_num, column_num, board)
33         self.__dfsPre(i_index, j_index-1, row_num, column_num, board)
34         self.__dfsPre(i_index, j_index+1, row_num, column_num, board)
35         
36     def __replace(self, row_num: int, column_num: int, board: List[List[str]])->None:
37         for i_index in range(row_num):
38             for j_index in range(column_num):
39                 if board[i_index][j_index] == 'O':
40                     board[i_index][j_index] = 'X'
41                 if board[i_index][j_index] == 'B':
42                     board[i_index][j_index] = 'O'
View Code

 

199. 二叉树的右视图

难度中等

给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例:

输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:

   1            <---
 /   \
2     3         <---
 \     \
  5     4       <---
 1 # Definition for a binary tree node.
 2 # class TreeNode:
 3 #     def __init__(self, x):
 4 #         self.val = x
 5 #         self.left = None
 6 #         self.right = None
 7 
 8 class Solution:
 9     def rightSideView(self, root: TreeNode) -> List[int]:
10         if not root:
11             return []
12         if not root.left and not root.right:
13             return [root.val]
14         
15         RRes = self.rightSideView(root.right)
16         LRes =  self.rightSideView(root.left)
17         if not LRes and RRes:
18             return [root.val] + RRes
19         elif LRes and not RRes:
20             return [root.val] + LRes
21         else:
22             temp = [LRes[i] for i in range(len(RRes), len(LRes)) ]
23             return [root.val] + RRes + temp
View Code

200. 岛屿数量

难度中等

给定一个由 '1'（陆地）和 '0'（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。

示例 1:

输入:
11110
11010
11000
00000

输出: 1

示例 2:

输入:
11000
11000
00100
00011

输出: 3
 1 class Solution:
 2     def numIslands(self, grid: List[List[str]]) -> int:
 3         if not grid:
 4             return 0
 5         Num = 0
 6         row_num = len(grid)
 7         column_num = len(grid[0])
 8 
 9         for i_index in range(row_num):
10             for j_index in range(column_num):
11                 if grid[i_index][j_index] == "1":
12                     self.__dfs(i_index, j_index, row_num, column_num, grid)
13                     Num = Num + 1
14 
15         return Num
16     
17     
18     def __dfs(self, i_index: int, j_index: int, row_num: int, column_num: int, board: List[List[str]])->None:
19         
20         if i_index < 0 or i_index >= row_num \
21             or j_index < 0 or j_index >= column_num \
22             or board[i_index][j_index] != "1":
23             return
24         board[i_index][j_index] = "2"
25         self.__dfs(i_index-1, j_index, row_num, column_num, board)
26         self.__dfs(i_index+1, j_index, row_num, column_num, board)
27         self.__dfs(i_index, j_index-1, row_num, column_num, board)
28         self.__dfs(i_index, j_index+1, row_num, column_num, board)
29
View Code

 


257. 二叉树的所有路径

难度简单

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例:

输入:

   1
 /   \
2     3
 \
  5

输出: ["1->2->5", "1->3"]

解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3
 1 # Definition for a binary tree node.
 2 # class TreeNode:
 3 #     def __init__(self, x):
 4 #         self.val = x
 5 #         self.left = None
 6 #         self.right = None
 7 
 8 class Solution:
 9     def binaryTreePaths(self, root: TreeNode) -> List[str]:
10         if not root:
11             return []
12         res = list()
13         self.binaryTreePathsPre(root, '', res)         
14         return res
15     
16     
17     def binaryTreePathsPre(self, root: TreeNode, path: str, res_temp: list) -> None:    
18         if not root:
19             return
20         if not root.left and not root.right:
21             res_temp.append(path + str(root.val))
22             return 
23         self.binaryTreePathsPre(root.left, path + str(root.val) +'->', res_temp)
24         self.binaryTreePathsPre(root.right, path + str(root.val) +'->', res_temp)
View Code

337. 打家劫舍 III

难度中等

在上次打劫完一条街道之后和一圈房屋后，小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为“根”。 除了“根”之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。

计算在不触动警报的情况下，小偷一晚能够盗取的最高金额。

示例 1:

输入: [3,2,3,null,3,null,1]

     3
    / \
   2   3
    \   \ 
     3   1

输出: 7 
解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.

示例 2:

输入: [3,4,5,1,3,null,1]

     3
    / \
   4   5
  / \   \ 
 1   3   1

输出: 9
解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.
 1 # Definition for a binary tree node.
 2 # class TreeNode:
 3 #     def __init__(self, x):
 4 #         self.val = x
 5 #         self.left = None
 6 #         self.right = None
 7 
 8 class Solution:
 9     def rob(self, root: TreeNode) -> int:
10         return max(self.__dfs(root))
11         
12     def __dfs(self, root: TreeNode)->(int,int):
13         if not root:
14             return 0, 0
15         if not root.left and not root.right:
16             return root.val, 0
17         
18         leftSelected, leftNotSelected = self.__dfs(root.left)
19         rightSelected, rightNotSelected = self.__dfs(root.right)
20         
21         rootSelected = root.val + leftNotSelected + rightNotSelected
22         rootNotSelected = max(leftSelected, leftNotSelected) + max(rightSelected, rightNotSelected)
23         return rootSelected, rootNotSelected
View Code

 

posted @ 2020-03-24 10:59  aiwenhua_0610  阅读(112)  评论(0)  编辑  收藏  举报