直线型一阶倒立摆4---能量起摆
五、能量起摆
能量起摆这一概念来自于K.J.Astrom and K.Furuta的SWINGING UP A PENDULUM BY ENERGY CONTROL。文献下载地址
以下是我翻译的部分论文。
摘要:这篇文章介绍了能量控制和展示了如何用该方法设计策略控制倒立摆起摆。
-
导论
倒立摆起摆是一个经典的控制学实验,see Furutaet al.(1992).Furutaet al的最小时间控制。这个。控制测量并不强健。这篇论文将要介绍能量控制问题。The pendulum is simply controlled in such a way that its energy is driven towards a value equal to the steady·state upright position.使用适当的控制策略可使倒立摆达到正确的位置。分析表明,这个问题完全可用两个参数表达。一个是time scale另一个是摆杆的最大加速与重力加速度之比。这个结论适用广义复杂的倒立摆。
2. PRELIMINARIES
考虑单级倒立摆。设它的质量为m,转动惯量关于枢轴点为j,并且设I为从枢轴到质心的距离。垂直和钟摆之间的夹角是θ,其中θ在时钟方向上是正的。重力加速度为g和质心加速度为u。
The equations of motion of the pendulum is 
系统有两个状态变量,角度θ和角速度![]() 。It is natural to let the state space be a cylinder.在这个状态空间中系统有两个平衡点为
。It is natural to let the state space be a cylinder.在这个状态空间中系统有两个平衡点为![]()
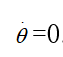 方程一基于许多假设,其中摩擦力忽略和假定倒立摆为刚体。同时也假定了轴向速度没有限制。
方程一基于许多假设,其中摩擦力忽略和假定倒立摆为刚体。同时也假定了轴向速度没有限制。
3.ENERGY CONTROL
多次测试表明能量控制倒立摆能够能够替代位置控制和速率,参见Wiklund et al.(1993).For example one way to swing the pendulum to the upright position is to give it an energy that corresponds to the upright position.倒立摆将起摆并在适当位置被稳摆算法控制。Equation (2).为了解决能量控制的有效性,需要理解质心加速度如何影响能量。Computing the deriva-tive of E with respect to time we find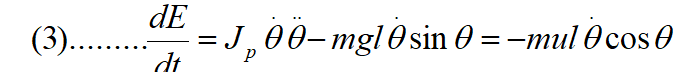
由式(3)可知,能量易于控制。该系统只是一个增益变化的积分器。当(3)的右边的u的系数消失时,就失去了可控性。
这发生在0 = 0或0 =±tr/2时,即,当摆是水平的或当它的速度逆转。当角B为0或ff且速度较大时,控制作用最为有效,为增加能量,当B cos{}为负时,主u的加速为正。
4.SWING UP STRATEGIES
我们现在要讨论让倒立摆上升到合适位置的方法。先假设倒立摆开始处于竖直稳定状态。倒立摆初始能量为-2mgl。(upright position)合适位置的能量为0.It is very convenient to use argu-ments based on control of the energy of the pendulum.(利用摆的能量控制原理进行论证是非常方便的。) 一种起摆的方法是控制倒立摆让它的能量从-2mgl增加到0.然后,倒立摆起摆到合适的位置会被稳摆程序捕获,并稳定倒立摆。可以看出,这类策略将收敛到期望的解决方案,见Fradkov(1991)和Frad-kov等(1995)。一个简单的方法就可以实现。假定倒立摆处于竖直位置。朝任意方向输出最大加速度,当速率变为零的时候然后颠倒加速度方向。(Accelerate with max-imum acceleration in an arbitrary direction and re-verse the acceleration when the velocity becomes zero. )为了了解这种策略会发生什么,我们引入一个固定在枢轴点上的坐标系。在这个坐标系中,摆的质心作圆周运动,如图l所示。如果加速度向右,则在OB方向上有一个磁场,其表观重力大小为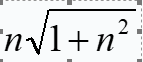 in the direction OB.然后钟摆对称地围绕OB摆动。考虑如下,倒立摆在A点时速率为0.倒立摆将摆到位置C角度为
in the direction OB.然后钟摆对称地围绕OB摆动。考虑如下,倒立摆在A点时速率为0.倒立摆将摆到位置C角度为![]() ,参加图一C点的速率将为0.此,钟摆的摆幅增加了一个相应的角度
,参加图一C点的速率将为0.此,钟摆的摆幅增加了一个相应的角度 为每一个反向的速度。注意,这个简单的策略只有在钟摆没有到达地平线时才是最优的,因为从式(4)可以看出,当钟摆水平时,加速度应该是反向的。还请注意,必须要求它是可能保持最大加速度在充分摆动。
为每一个反向的速度。注意,这个简单的策略只有在钟摆没有到达地平线时才是最优的,因为从式(4)可以看出,当钟摆水平时,加速度应该是反向的。还请注意,必须要求它是可能保持最大加速度在充分摆动。
5.SINGLE-SWING BEHAVIOR
摆升的行为主要取决于枢轴的最大加速度。如果参数n足够大,就能很快地获得所需的能量,而且摆可以一次摆起来,但如果n很小,则需要多次摆起来。
Double-Switch Control
如果加速度足够的大,在输出最大加速度的情况下倒立摆很容易起摆,直到获得期望能量,再将加速度设置为0.使用这种方法控制信号开关从0变到最大值,再从最大值变为0.这也是该方法命名的缘由。找到这个策略,我们将考虑一个固定在摆的枢轴上的坐标系,并把由于枢轴加速度产生的力看作是一个外力。在这个坐标系中,摆的质心沿半径为I的圆周运动。由式(4)可知,摆达到水平位置前必须达到所需要的能量。如果支点的加速度一直保持在最大值ng,直到达到水平,支点的加速度提供给摆的能量为nmgl。摆上摆的能量必须增加2mgl,因此我们发现最大加速度必须至少是2g。当加速度为2g时,摆被加速到水平,此时控制信号为零。如果加速度大于2g,当摆摆角ф时,加速度将被关闭。提供给摆的能量是nmgl sinф。Equating this with 2mgl gives 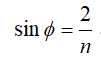 。单开关双开关策略如图2所示,它给出了n = 2.1时的角度、角速度和控制信号。注意,在达到所需的能量之前使用最大控制动作。这发生在钟摆水平之前。
。单开关双开关策略如图2所示,它给出了n = 2.1时的角度、角速度和控制信号。注意,在达到所需的能量之前使用最大控制动作。这发生在钟摆水平之前。

Large Accelerations
如果可用加速度远远大于2g,就有可能找到开关时间的近似表达式。我们将考虑钟摆从向下的位置开始时的情况。
如果加速度如此之大,以致于在小角度下可以得到所需的能量,则运动方程(1)可以近似为 
这个方程的解 。倒立摆能量增加为
。倒立摆能量增加为 。使它等于起摆能量2mgl.求得完全加速时间为
。使它等于起摆能量2mgl.求得完全加速时间为 

其中![]() 为摆小振动的频率,摆改变角度
为摆小振动的频率,摆改变角度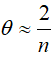 比较精确值
比较精确值 )。当n = 10时,我们得到e.g。在加速过程中,给定的加速度让倒立摆摆动了11.5°。
)。当n = 10时,我们得到e.g。在加速过程中,给定的加速度让倒立摆摆动了11.5°。
Triple-Switch Control
在上面讨论的单摆策略中,摆向一边并继续摆,直到摆到垂直位置。即使最大加速度小于2g,也有可能找到钟摆以同方式运动的策略。然而,控制信号会切换几次。加速度必须大于g,才能使摆在一次摆动中达到水平。“磅找出更大的是我们将考虑情况如图3所示,钟摆开始在其他位置,最大加速度ng首次应用于积极的方向,一个观察者固定在主蜜蜂的引力场OB方向的能量 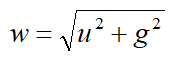
当摆锤从A移动到D时,它失去势能mwa = mw(sinθ -cosθ),它被转换为动能,从公式(3)得出,枢轴的控制加速度应该反转当摆锤是水平的,以便最大化摆锤的能量。当加速度反转时,固定在枢轴上的观察者看到OC方向上的重力场,摆锤的动能必须足够大才能带来摆到位置E.势能的差异是mwb,因此我们得到条件a> b。从图3可以得出 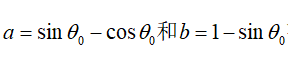
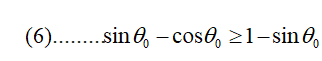
引入![]()

该等式具有解n = 4/3。因此,加速度必须至少为4g/3才能具有单摆行为。当加速度恰好等于4g /3时,枢轴将首先向右加速,直到摆锤到达水平位置。然后反转加速直到摆锤达到所需的能量,当a,'celeration设置为零时,当n大于4/3时,摆锤的加速度可以在摆锤到达点K之前设置为零当枢轴的加速度设定为零时,让摆锤与水平面形成角度ф。提供给摆的能量则为mgl(2-sin ф),因为枢轴通过加速度移动距离1+ L(l-sinф),等于2mgl给出
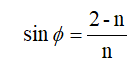
For n = 4/3 we get ф = 30' .
单摆三开关控制如图4所示。最初施加最大控制信号。能量增加但是当摆锤是水平时它没有达到期望的水平。 'lb继续向钟摆供电,然后反转控制信号,直到获得所需的能量。然后将控制信号设置为零。由于对于这种类型的行为,n = 2.1接近极限n = 2,当控制信号设置为零时,摆锤接近期望的直立位置。
6.MULTI-SWING BEHAVIOR
如果最大加速度小于4g / 3,则需要在摆锤到达直立位置之前多次摆动摆锤。让我们首先考虑将摆锤放在图5所示的两个摆动中的条件,图5显示了固定在枢轴上的坐标系。该坐标系中的观察者看到强度![]() 。如果枢轴的加速度为正,则磁场具有方向OB,而当磁极为负时,该磁场具有方向OC。假设摆锤在A处静止时开始,并且首先在正方向上给出最大加速度。然后钟摆在图中从A摆动到C.此时摆锤转动,枢轴的加速度反转。当摆锤在E处到达水平位置时,枢轴的加速度再次反转。如果E处的速度足够大,则钟摆将达到直立位置。钟摆在D处休息时。当它移动到E时,它已经失去了潜在的能量mwa,它已被转移到动能。这个动能必须足够大才能将摆锤移动到F.这个能量是mwb,我们得到条件b≥a。从图5可以看出a = sin
。如果枢轴的加速度为正,则磁场具有方向OB,而当磁极为负时,该磁场具有方向OC。假设摆锤在A处静止时开始,并且首先在正方向上给出最大加速度。然后钟摆在图中从A摆动到C.此时摆锤转动,枢轴的加速度反转。当摆锤在E处到达水平位置时,枢轴的加速度再次反转。如果E处的速度足够大,则钟摆将达到直立位置。钟摆在D处休息时。当它移动到E时,它已经失去了潜在的能量mwa,它已被转移到动能。这个动能必须足够大才能将摆锤移动到F.这个能量是mwb,我们得到条件b≥a。从图5可以看出a = sin ![]() -cos 3
-cos 3![]() 和b = 1 -sin
和b = 1 -sin ![]() 。
。
因此
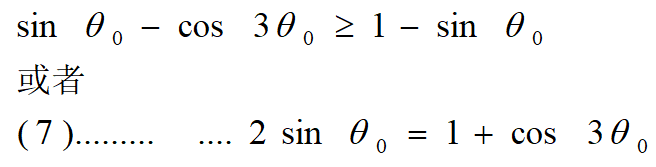
该等式具有解决方案![]() 。因此所需的最大加速度为0.58g。控制信号在该策略中切换四次,因为必须在D处反向控制以减小摆的能量。
。因此所需的最大加速度为0.58g。控制信号在该策略中切换四次,因为必须在D处反向控制以减小摆的能量。
The General Case
很容易将论证扩展到需要更多波动的情况。例如,在具有三次摆动的策略中,钟摆首先在一个方向上摆动2![]() 。下一次向另一个方向摆动4
。下一次向另一个方向摆动4![]() ,到达直立位置的状态变为
,到达直立位置的状态变为
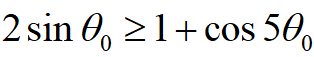
A case with k swings gives the equation
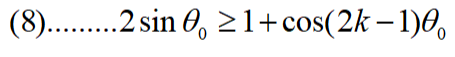


以数字方式求解该等式,我们得到以下值: 
对于n的小值,n和k之间的关系近似由下式给出

所需的开关数量随着n的减小而增加。当n = 0.25时,我们发现需要五个开关来摆动摆锤。这在图6中示出了图示。
7.MINIMUM TIME STRATEGIES
从Pontryagins最大原则可以看出,摆锤摆动的最小时间策略是bang-bang型。可以证明,这些策略可以很好地解释为能量控制。它们将以最大速率向钟摆注入能量,然后以最大速率移除能量,使得当达到直立位置时能量对应于平衡能量。对于n的小值,最小时间策略给出的控制信号与最初基于能量控制的策略相同。然而,控制信号的最后部分是不同的,因为我们已经描述的策略将在获得所需能量时将控制信号设置为零。因此,所给出的策略可以被描述为能量中没有过冲的策略。
考虑例如情况n> 2,其中可以使用单摆动策略。 10摆动pendu-lum它的能量必须增加2mgl。这可以通过Fignre 2中所示的单摆双开关策略来实现。最大加速度一直使用,直到摆锤移动角度arctan2 / n。通过继续加速可以进一步增加能量,直到摆锤到达水平位置。从方程(3)得出,加速度应该相反。通过将加速度反转到适当的位置,可以减小能量,使得当摆锤处于水平时它达到所需的值。通过计算细节,我们发现角度获得了最大能量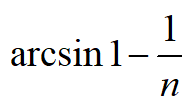
然后以最大速率降低能量。图7比较了最小时间策略和能量控制策略。该图还显示,到达直立位置的时间差异随着n的增加而增加。它还表明最小时间策略的能量过冲。过冲随着n的增加而增加。对于n = 5的情况,过冲超过200%。这就解释了为什么最小时间策略非常敏感。当钟摆接近右上位置时,多余的能量迅速消失。能量控制为直立位置提供了更多的方法。通常结合几种不同的策略来摆动钟摆。当钟摆接近直立位置时使用捕捉策略。一个好的实践方法是使用能量超过10-20%的能量控制策略,并在接近垂直位置时抓住笔杆。这种策略很简单,对于建模工具非常有用。 
8.CONCLUSION
已经表明,通过控制其能量来摆动摆锤是非常方便的。由等式(4)给出的控制策略非常简单。使用此策略获得的行为主要取决于一个参数,即可用的加速度。如果加速度足够大,u> 2g,摆锤可以一次摆动到达直立位置。控制信号使用其最大值,直到获得所需的能量,然后设置为零。对于u> 4g / 3,摆锤仍可以一次摆动,但控制信号现在可以制作三个开关。对于较低的加速度,摆锤必须摆动几次。
9. 参考文献
K. Furuta, M. Yamakita, and S. Kobayashi (1992), Swing-up control of inverted pendulum using pseudo-state feed-back. J. Systems and Control Eng. 206, pp. 263-269. M. Wiklund, A. KristenBon, and K. J. Astrom (1992, A new strategy for swinging up an inverted pendulum. Proc. IFAC 12th World Congress, Vo\. 9, pp. 151-154. Fradkov, A. L. (1991), Speed-gradient laws of control and evolution. Proc. 1st European Control Conference, Greno-ble, pp. 1861-1865. Fradkov, A. L., P. Y. Guzenko, D. J. Hill, and A. y. Pogromsky (1995), Speed gradient control and passivity of nonlinear oscillators. Proc. IFAC Symposium on Control of Nonlinear Systems, Lake Tahoo.
其它博文链接:直线型一阶倒立摆1---概念篇
直线型一阶倒立摆2---建模
直线型一阶倒立摆3---控制器设计
有需要直线型一阶倒立摆的VREP仿真文件:可点击


 浙公网安备 33010602011771号
浙公网安备 33010602011771号