Dechin的博客

摘要： 本文通过几个示例，介绍了在Python、Numpy和PyTorch三个不同的框架下，对于求余数函数的定义。比较特殊的是pytorch中的fmod函数，并不符合数学上的求余数方法，而是需要使用remainder函数。 阅读全文

摘要： 本文介绍了在Python的classmethod装饰的类方法的cls变量的意义，通过几个不同的示例对比，凸显cls变量在Python编程中的应用场景。对于大多数的场景来说，使用普通的Python类和函数定义即可。如果需要在类的外部使用类的内部函数，但是可能有多个不同初始化的类输入，那么可以使用staticmethod进行装饰。如果只有一个类，而有多种不同的输入场景下，可以使用classmethod进行装饰。 阅读全文

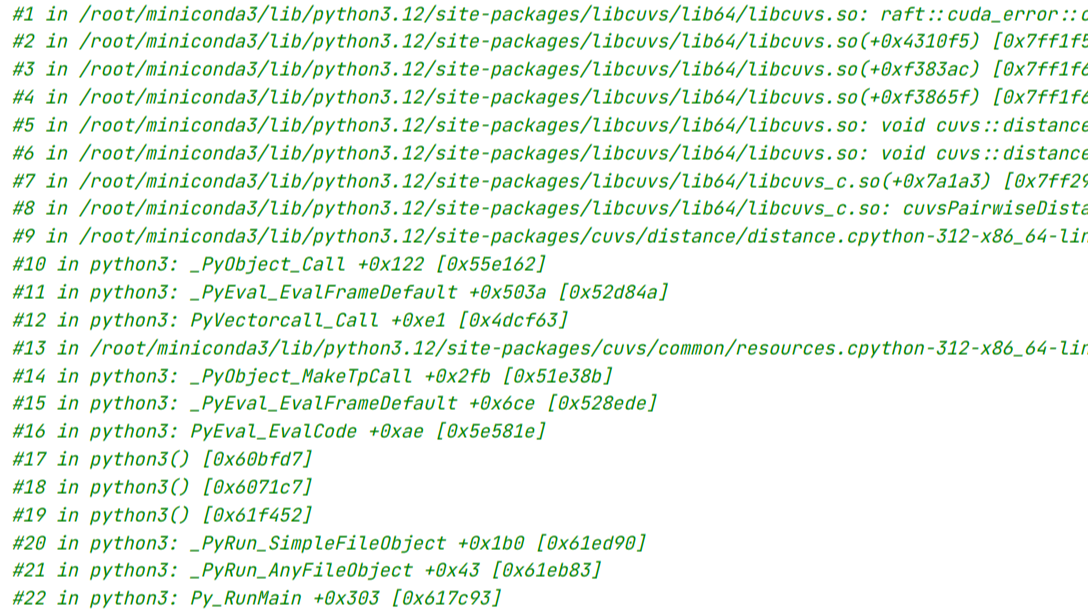摘要： 本文记录了一些使用python-cupy的过程中有可能的遇到的一些问题，一部分是环境配置问题，还有一部分是运行输入问题。 阅读全文

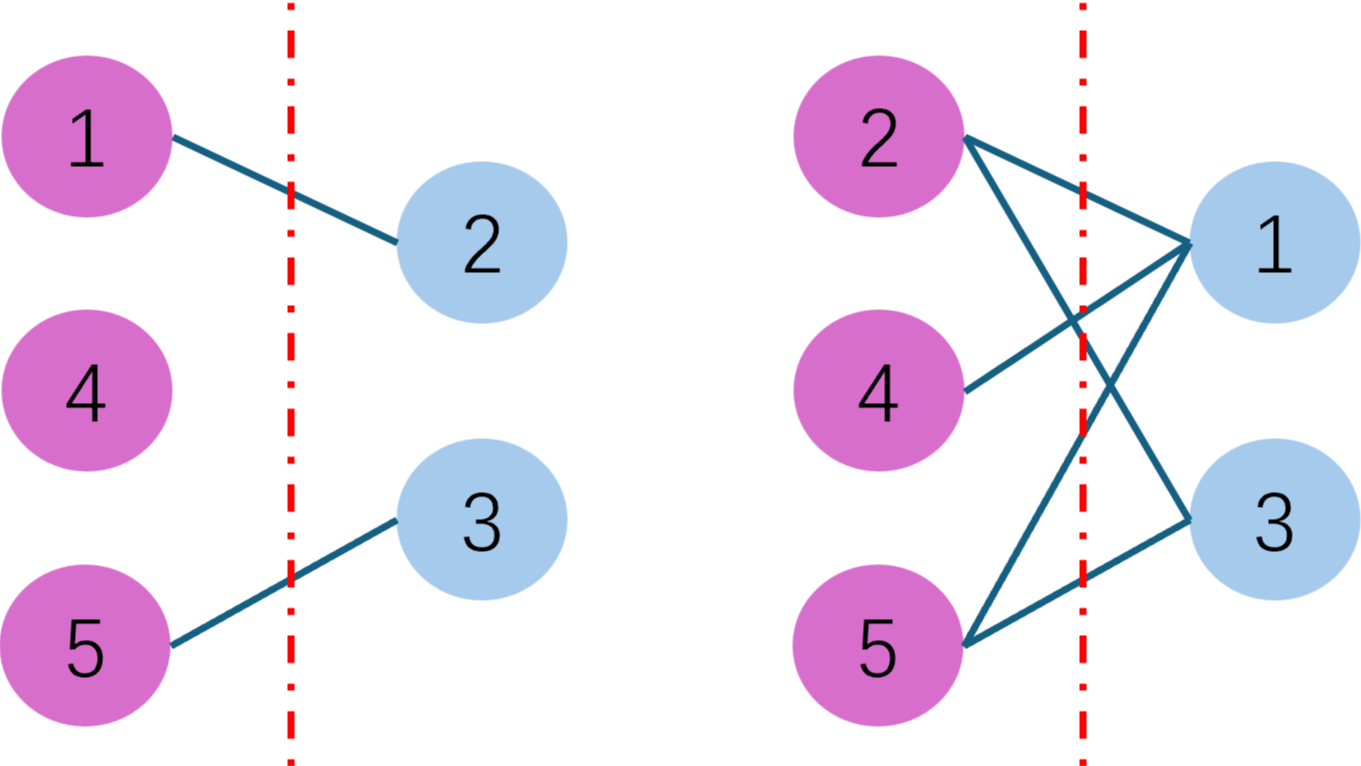摘要： 这篇文章算是对Fred Glover的一篇综述的解读，添加了一些方便直观理解的示例具体的建模过程。对于不同的场景，可以使用不同的惩罚项进行QUBO建模，从而可以使用求解器或者Ising机进行求解。 阅读全文

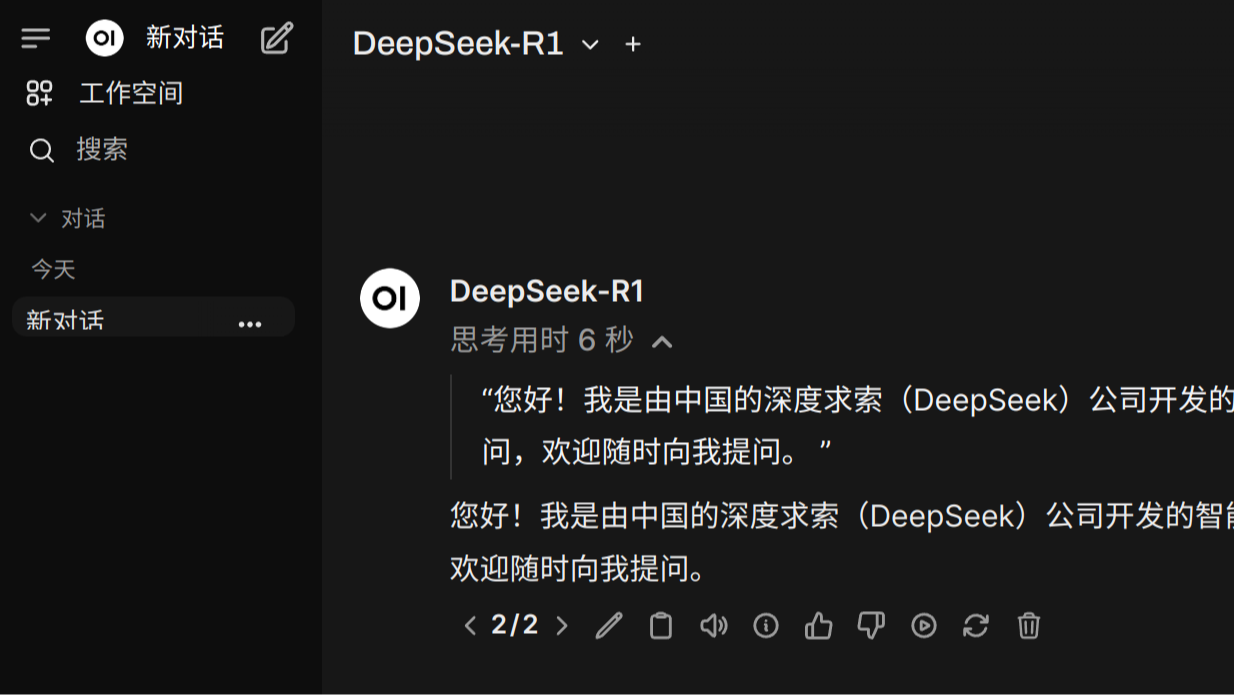摘要： 本文介绍了国产的大模型推理工具KTransformers在本地成功运行的一个案例，在容器化部署的基础上，结合Open WebUI做了一个用户友好的大模型服务。 阅读全文

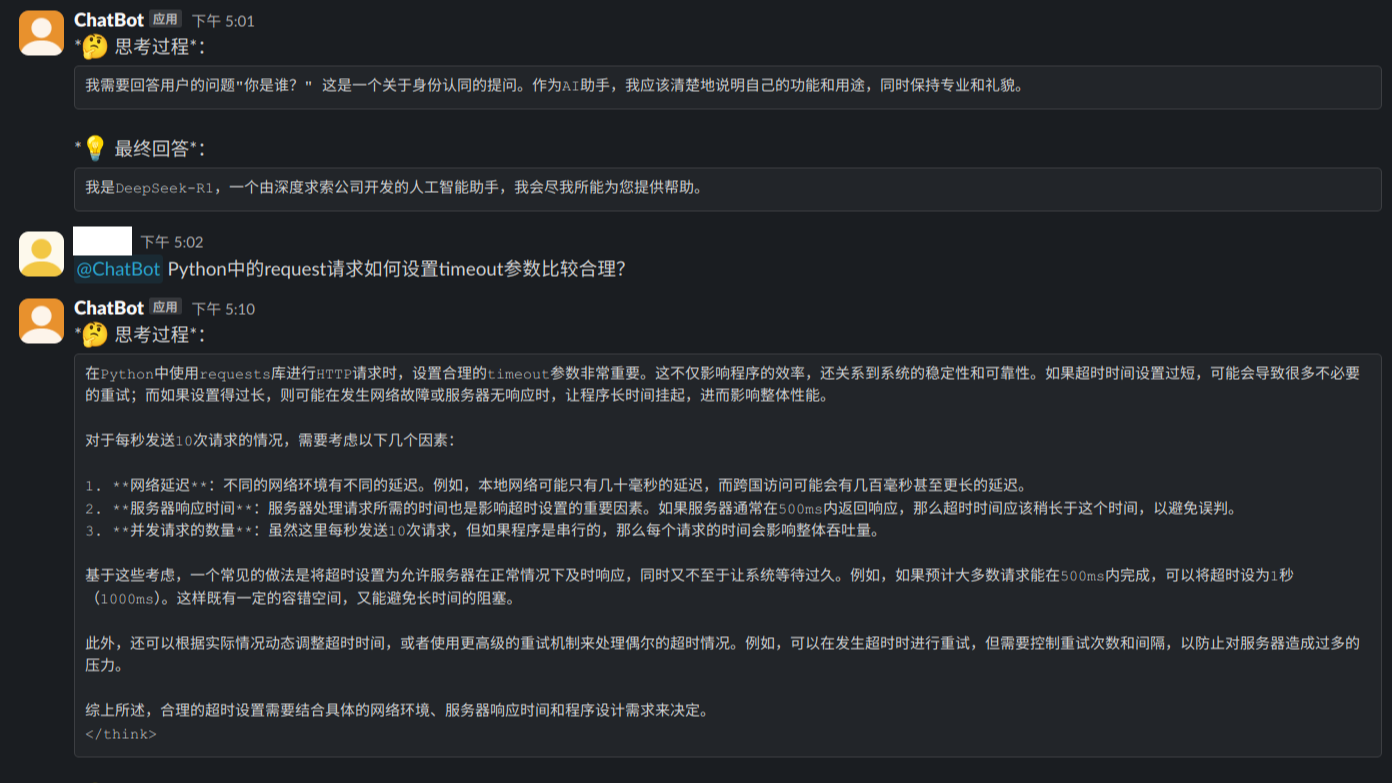摘要： 本文介绍了一种使用Slack聊天工具中的机器人SlackBot的API接口，实现本地化部署Ollama的DeepSeek大模型的远程通讯方案。相比于调用公网的API接口，数据隐私稍微好一点点。最终的方案应该是自建加密聊天工具+Ollama本地化部署，但是这个时间成本有点高，用户可以自行尝试。 阅读全文

摘要： 本文介绍了使用CUDA和Cython来实现一个CUDA加法算子的方法，并介绍了使用CUDA参数来估算性能极限的算法。经过实际测试，核函数部分的算法性能优化空间已经不是很大了，更多时候可以考虑使用Stream来优化Host和Device之间的数据传输。 阅读全文

摘要： 以学习CUDA为目的，接上一篇关于Cython与CUDA架构下的Gather算子实现，这里我们加一个Batch的维度，做一个BatchGather的简单实现。 阅读全文

摘要： 本文收集了一些目前为止仅有DeepSeek满血版可以正确答复的“简单问题”，以供测试和验证自己所使用的模型是满血版DeepSeek还是残血版的DeepSeek。有两点需要提示：各大厂商模型可以联网更新，本问题集有一定的时效性；部分数学和推理类问题，跟temperature参数的设定有关，temperature参数设置的越低，回答越严谨。 阅读全文

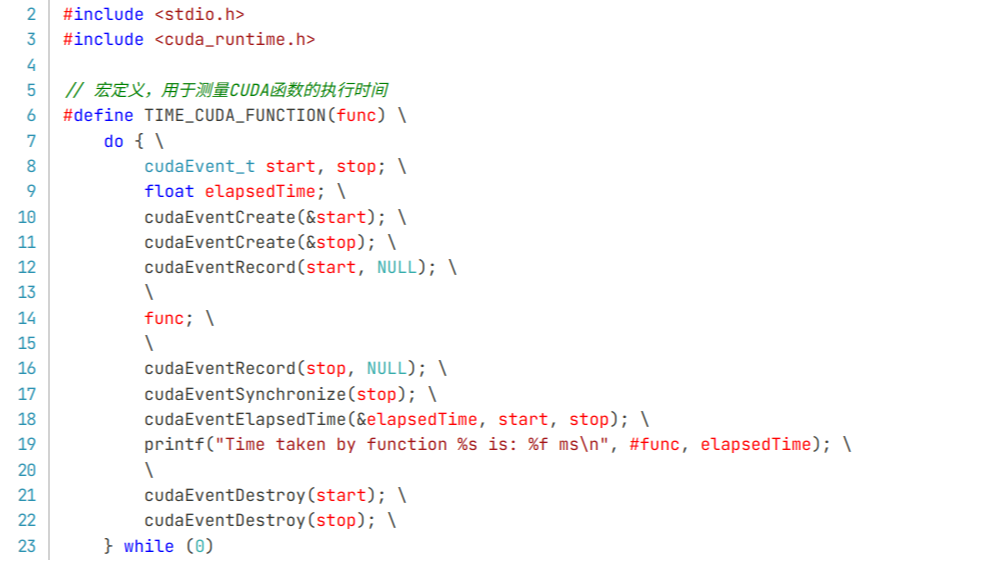摘要： 这篇文章主要介绍了一个CUDA入门的技术：使用CUDA头文件写一个专门用于CUDA函数运行时长统计的宏，这样就可以统计目标Kernel函数的运行时长。可以直接在CUDA中打印相应的数值，也可以回传到Cython或者Python中进行打印。 阅读全文

摘要： 本文使用了Cython作为封装函数，封装一个CUDA C实现的Gather算子，然后通过Python去调用，用这种方法实现一个比较Pythonic的CUDA Gather函数的实现和调用。 阅读全文

摘要： 本文主要介绍了在CUDA编程的实践中，增加一个异常捕获的宏模块，以保障CUDA项目结果的准确性。主要代码内容参考了樊哲勇所著的《CUDA编程基础与实践》，是一本很好的CUDA编程入门书籍。 阅读全文

摘要： 本文介绍了一种将Hugging Face上bin格式的大模型文件，在线转换为safetensors文件格式，然后下载到本地的方法。 阅读全文

摘要： 对于本地模型的加载来说，除了使用KTransformer等工具进行指令集层面的优化之外，还可以调整模型加载层数，做一个简单的优化。这里提供了一个num_gpu和num_ctx参数调整的策略，实测Tokens性能最大可优化10倍左右。 阅读全文

摘要： 为了方便本地大模型部署和迁移，本文提供了一个关于Ollama的模型本地迁移的方法。由于直接从Ollama Hub下载下来的模型，或者是比较大的GGUF模型文件，往往会被切分成多个，而文件名在Ollama的路径中又被执行了sha256散列变换。因此我们需要从索引文件中获取相应的文件名，再进行模型本地迁移。 阅读全文