PCA主成分分析的Python实现

技术背景

PCA主成分分析在数据处理和降维中经常被使用到，是一个非常经典的降维算法，本文提供一个PCA降维的流程分解，和对应的Python代码实现。

二维数据生成

如果没有自己的测试数据，我们可以生成一些特殊的随机数据点。例如我们使用Numpy的均匀随机数生成一系列二维的数据点\(\mathbf{r}=\left(x,y\right)\)，其中数据点分布在一个椭圆内：

\[x^2+4y^2\leq 1 \]

生成数据点的Python代码如下所示：

import numpy as np

def plot_points(data):
    import matplotlib.pyplot as plt
    plt.figure()
    plt.xlim(-1, 1)
    plt.ylim(-1, 1)
    plt.plot(data[:, 0], data[:, 1], '.', color='blue')
    plt.savefig("PCA.png")

def data_generator(nodes, seed=0):
    np.random.seed(seed)
    data = 2 * np.random.random((nodes, 2)) - 1
    mask_index = np.where(data[:,0]**2+4*data[:,1]**2<=1)[0]
    masked_data = data[mask_index]
    return masked_data

if __name__ == "__main__":
    masked_data = data_generator(1000)
    plot_points(masked_data)

运行上述代码会在当前路径下生成一个PCA.png的图片，结果如下所示：

数据标准化

因为不同类型的数据有不同的范围和特征，可以做一个标准化方便后续处理，但标准化之后的数据，记得降维之后要进行还原：

\[\mathbf{x}'=\frac{x-\bar{x}}{\sqrt{\frac{\sum_i(x-\bar{x})^2}{n-1}}} \]

这是\(x\)方向的标准化，\(y\)方向的标准化同理，最终可以得到\(\mathbf{Z}=\left(\mathbf{x}',\mathbf{y}'\right)\)。对应的Python函数实现为：

def normalization(data):
    data_avg = np.average(data, axis=0)
    data_shift = data - data_avg
    output = np.zeros_like(data)
    for i in range(data.shape[-1]):
        output[:, i] = data_shift[:, i] / np.sqrt(np.sum(data_shift[:, i] ** 2)/(data.shape[0]-1))
    return output

协方差矩阵

正常我们写样本协方差矩阵的形式是这样的：

\[C_{jk}=\frac{\sum_{i=1}^n(x_{ij}-\bar{x})(y_{ik}-\bar{y})}{n-1} \]

但是因为前面已经分别得到了两个方向的标准化数据，所以我们直接用下面这个公式计算就可以了：

\[C=\frac{Z^TZ}{n-1} \]

对应的Python实现为：

def cov_matrix(Z):
    return (Z.T @ Z) / (Z.shape[0] - 1)

如果对标准化之后的数据计算一个协方差矩阵可以得到：

[[1.         0.04955086]
 [0.04955086 1.        ]]

特征值分解

关于特征值分解的内容，可以参考上一篇文章中的介绍。总体来说就是把一个矩阵分解为如下形式：

\[C=U\Sigma U^{-1} \]

其中\(\Sigma\)是由本征值组成的对角矩阵，\(U\)是由本征列向量组成的本征矩阵。对应的Python代码实现为：

def eig_decomp(C):
    vals, vecs = np.linalg.eig(C)
    sort_idx = np.argsort(vals)
    return np.diag(vals), vecs, sort_idx

如果对上面的协方差矩阵做一个特征值分解，可以得到输出的特征值为：

[[1.04955086 0.        ]
 [0.         0.95044914]]

输出的特征列向量组成的矩阵\(U\)为：

[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

可以把这两个列向量画到数据点中：

PCA降维

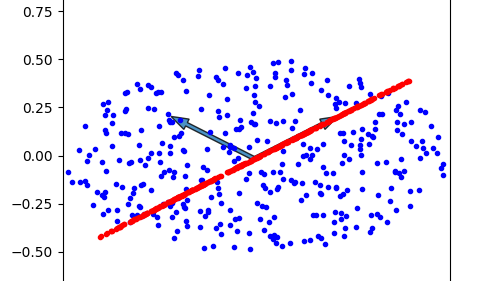
根据上面生成的对角化矩阵，我们已经可以从中筛选一些比较大的值和对应的本征向量，作为数据点的“主要成分”。一般是在本征值之间的值差异较大的时候可以更好的降维，这里生成的数据其实两个本征值没有很好的降维效果，但是我们依然可以执行降维的操作。例如我们选取第一个本征向量\(\mathbf{v}\)作为投影空间，把所有的数据点都投影到这个向量上：

\[\mathbf{r}'=\bar{\mathbf{r}}+\frac{(\mathbf{r}-\bar{\mathbf{r}})\cdot\mathbf{v}}{|\mathbf{v}|^2}\mathbf{v} \]

就可以完成对数据点的降维，效果如下所示：

所用到的完整Python代码示例如下：

PCA Python完整代码

import numpy as np

def plot_points(data):
    import matplotlib.pyplot as plt
    plt.figure()
    plt.xlim(-1, 1)
    plt.ylim(-1, 1)
    plt.plot(data[:, 0], data[:, 1], '.', color='blue')
    plt.savefig("PCA.png")

def plot_vec(data, center, vecs):
    import matplotlib.pyplot as plt
    plt.figure()
    plt.xlim(-1, 1)
    plt.ylim(-1, 1)
    plt.plot(data[:, 0], data[:, 1], '.', color='blue')
    for i in range(vecs.shape[-1]):
        plt.arrow(center[0], center[1], vecs[:,i][0], vecs[:,i][1], width=0.02, alpha=0.8)
    plt.savefig("PCA.png")

def plot_reduced(data, center, vec_proj, vecs):
    import matplotlib.pyplot as plt
    plt.figure(figsize=(5,5))
    plt.xlim(-1, 1)
    plt.ylim(-1, 1)
    plt.plot(data[:, 0], data[:, 1], '.', color='blue')
    vec_proj += center
    plt.plot(vec_proj[:, 0], vec_proj[:, 1], '.', color='red')
    for i in range(vecs.shape[-1]):
        plt.arrow(center[0], center[1], vecs[:,i][0], vecs[:,i][1], width=0.02, alpha=0.8)
    plt.savefig("PCA.png")

def data_generator(nodes, seed=0):
    np.random.seed(seed)
    data = 2 * np.random.random((nodes, 2)) - 1
    mask_index = np.where(data[:,0]**2+4*data[:,1]**2<=1)[0]
    masked_data = data[mask_index]
    return masked_data

def normalization(data):
    data_avg = np.average(data, axis=0)
    data_shift = data - data_avg
    output = np.zeros_like(data)
    sigmai = np.zeros(data.shape[-1])
    for i in range(data.shape[-1]):
        sigmai[i] = np.sqrt(np.sum(data_shift[:, i] ** 2)/(data.shape[0]-1))
        output[:, i] = data_shift[:, i] / sigmai[i]
    return output, data_avg, sigmai

def cov_matrix(Z):
    return (Z.T @ Z) / (Z.shape[0] - 1)

def eig_decomp(C):
    vals, vecs = np.linalg.eig(C)
    sort_idx = np.argsort(vals)
    return np.diag(vals), vecs, sort_idx

def dimension_reduction(data, center, v):
    return np.einsum('ij,j->i', data-center, v/np.linalg.norm(v))[:,None] * v[None]/np.linalg.norm(v)

if __name__ == "__main__":
    masked_data = data_generator(1000)
    normalized_data, center, sigmai = normalization(masked_data)
    C = cov_matrix(normalized_data)
    Sigma, U, idx = eig_decomp(C)
    reduced_data = dimension_reduction(masked_data, center, (U*sigmai[:,None])[:, 0])
    plot_reduced(masked_data, center, reduced_data, U*sigmai[:,None])

总结概要

接上一篇文章介绍的矩阵特征分解，本文介绍了矩阵特征分解在主成分分析（PCA）算法中的应用。对于PCA算法，最直观的理解就是，在高维数据中找到一个低维的空间，使得所有的数据点投影到该低维空间之后尽可能的分离。

版权声明

本文首发链接为：https://www.cnblogs.com/dechinphy/p/pca.html

作者ID：DechinPhy

更多原著文章：https://www.cnblogs.com/dechinphy/

请博主喝咖啡：https://www.cnblogs.com/dechinphy/gallery/image/379634.html