学习率衰减加冲量优化的梯度下降法Python实现方案

应用场景

优化算法经常被使用在各种组合优化问题中。我们可以假定待优化的函数对象\(f(x)\)是一个黑盒，我们可以给这个黑盒输入一些参数\(x_0, x_1, ...\)，然后这个黑盒会给我们返回其计算得到的函数值\(f(x_0), f(x_1), ...\)。我们的最终目的是得到这个黑盒函数的最优输入参数\(x_i\)，使得\(f(x_i)=min\{f(x)\}\)。那么我们就会想到，通过不断的调整输入给黑盒的\(x\)值，直到找到满足要求的那个\(x\)值。

我们需要明确的一个信息是，我们不可能遍历这整个的函数空间。虽然这样能够使得我们找到真正的最优解，但是遍历所带来的时间消耗是一般的项目所无法接受的，因此就需要一些更加聪明的变化方法来对黑盒进行优化。

梯度下降法

梯度下降(Gradient Descent)是最早被提出的一种简单模型，其参数迭代思路较为简单：

\[x_{n+1} = x_{n} - \gamma\frac{d}{dx}f(x_n) \]

或者也可以将其写成更加容易理解的差分形式：

\[x_{n+1} = x_{n} - \gamma\frac{f(x_{n+1})-f(x_n)}{x_{n+1}-x_{n}} \]

其中的\(\gamma\)我们一般称之为学习率，在后续的博客中，会介绍一种自适应学习率的梯度优化方法。学习率会直接影响到优化收敛的速率，如果设置不当，甚至有可能导致优化结果发散。我们在优化的过程中一般采用自洽的方法，使得优化过程中满足自洽条件后直接退出优化过程，避免多余的计算量：

\[\frac{d}{dx}f(x_n)=0 \]

在该条件下实际上我们找到的很有可能是一个局部最优值，在minimize的过程中可以认为是找到了一个极小值或者常见的鞍点(如下图所示)。如果需要跳出极小值，可能需要额外的方法，如随机梯度下降和模拟退火等。

针对梯度下降算法的改进

实际应用中如果直接使用该梯度下降算法，会遇到众多的问题，如：在接近极小值附近时优化过程缓慢，或者由于步长的设置导致一致处于"震荡"的状态，这里我们引入两种梯度下降的优化方案。

衰减参数的引入

由于前面提到的梯度下降算法的学习率\(\gamma\)是固定的，因此在迭代优化的过程中有可能出现这几种情况：

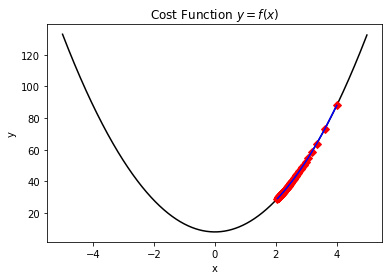
1. 由于设置的学习率太小，导致一直出于下降优化过程，但是直到达到了最大迭代次数，也没能优化到最优值。如下图所示，正因为学习率设置的太低而导致迭代过程无法收敛。
   
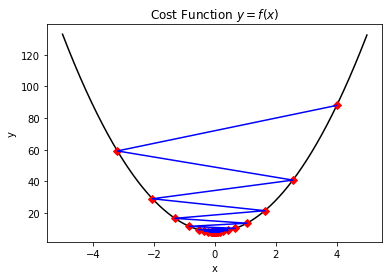
2. 由于设置的学习率太大，导致出现"震荡"现象，同样无法尽快优化到收敛值。
   

因此，这里我们可以引入衰减参数的概念，使得梯度下降的过程中，学习率也逐步的在衰减，越靠近收敛值跳动就越缓慢：

\[x_{n+1} = x_{n} - \frac{\gamma}{n+1}\frac{f(x_{n+1})-f(x_n)}{x_{n+1}-x_{n}} \]

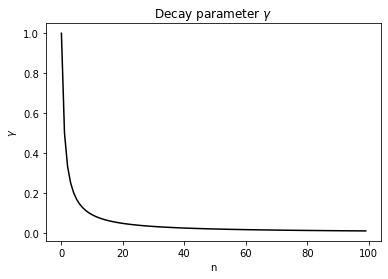
在这种配置下，学习率参数\(\gamma\)按照如下图所示的趋势进行衰减：

import matplotlib.pyplot as plt
x = [i for i in range(100)]
y = [1/(i + 1) for i in range(100)]
plt.figure()
plt.plot(x,y,color='black')
plt.title('Decay parameter $\gamma$')
plt.xlabel('n')
plt.ylabel('$\gamma$')
plt.show()

冲量参数的引入

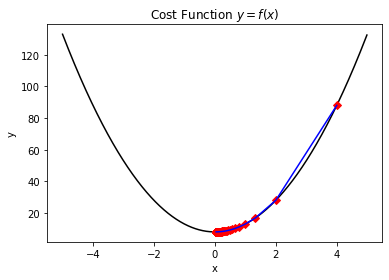
在迭代优化的过程中，靠近极小值处的优化效率也是一处难点，也正是因为配置了衰减参数，因此在优化的末尾处会尤其的缓慢(如下图所示)。为此，我们需要一些提高效率的手段。

首先我们可以尝试结合一些物理定律来考虑这个问题，比如冲量定理：

\[Ft=m\frac{d}{dt}x_1-m\frac{d}{dt}x_0 \]

这个经典力学公式所隐藏的一个规律是：当我们给定一个"迭代冲量"时，本次迭代过程的偏移量\(\frac{d}{dt}x_1\)的大小跟前面一次的偏移量\(\frac{d}{dt}x_0\)是有一定的关系的。因此这里我们也添加一个"冲量"参数，使得如果前一次梯度前进的方向与本次前进方向相同，则多前进一些步长，而如果两者梯度方向相反，则降低步长以防止"震荡"现象。具体公式变动如下所示：

\[x_{n+1} = x_{n} - \frac{\gamma}{n+1}\frac{f(x_{n+1})-f(x_n)}{x_{n+1}-x_{n}} + m(x_{n}-x_{n-1}) \]

在给定上述的迭代策略之后，我们可以开始定义一些简单的问题，并使用该梯度下降的模型去进行优化求解。

定义代价函数

这里我们开始演示梯度下降法的使用方法，为此需要先定义一个代价函数用于黑盒优化，我们可以给定这样的一个函数：

\[f(x)=5x^2+8 \]

这个函数所对应的python代码实现如下：

import matplotlib.pyplot as plt

def cost_function(x):
    return 5 * x ** 2 + 8

plt.figure()
x = [i / 100 - 5 for i in range(1000)]
y = [cost_function(i) for i in x]
plt.plot(x, y, color = 'black')
plt.title('Cost Function $y = f(x)$') # Latex Type Equation.
plt.xlabel('x')
plt.ylabel('y')
plt.show()

从上述python代码的输出中，我们可以看到该函数的轮廓结构如下图所示：

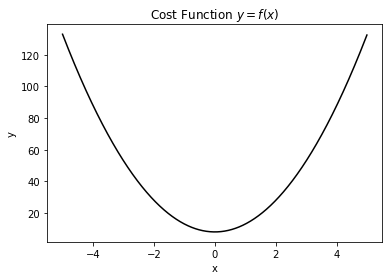
从图中我们可以获取大概这些信息：函数连续可微，存在极小值且为最小值，最小值对应的输入在0附近。

梯度下降法的代码实现

根据算法特性，我们将其分为了参数定义、代价函数定义、梯度计算、路径计算几个模块，最终再将其集成到minimize函数中。此处我们还额外引用了scipy.optimize.minimize函数作为一个对比，以及tqdm可用于展示计算过程中的进度条，相关使用方法可以参考这篇博客。

from scipy.optimize import minimize as scipy_minimize
from tqdm import trange
import matplotlib.pyplot as plt
import numpy as np

DELTA = 1e-06
EPSILON = 1e-06
MAX_STEPS = 100
GAMMA = 0.6
MOMENTUM =0.2

def cost_function(x):
    return 5 * x ** 2 + 8

def gradient(x, func):
    return (func(x + DELTA) - func(x)) / DELTA

def next_x(x, func, iterations, v):
    _tmpx = x - GAMMA  * gradient(x, func) / (iterations + 1) + MOMENTUM * v
    return _tmpx if cost_function(_tmpx) < cost_function(x) and gradient(_tmpx, func) * gradient(x, func) >= 0 else x

def minimize(x0, func):
    _x1 = x0
    _y1 = func(_x1)
    plot_x = [_x1]
    plot_y = [_y1]
    v = 0
    for i in trange(MAX_STEPS):
        _x = next_x(_x1, func, i, v)
        _y = func(_x)
        v = _x - _x1
        if v == 0:
            continue
        if abs(_y - _y1) <= EPSILON:
            print ('The minimum value {} founded :)'.format(_y))
            print ('The correspond x value is: {}'.format(_x))
            print ('The iteration times is: {}'.format(i))
            return _y, _x, plot_y, plot_x
        _x1 = _x
        _y1 = _y
        plot_x.append(_x1)
        plot_y.append(_y1)
    print ('The last value of y is: {}'.format(_y))
    print ('The last value of x is: {}'.format(_x))
    return _y, _x, plot_y, plot_x

if __name__ == '__main__':
    x0 = 4
    yt, xt, py, px = minimize(x0, cost_function)
    plt.figure()
    x = [i / 100 - 5 for i in range(1000)]
    y = [cost_function(i) for i in x]
    plt.plot(x, y, color = 'black')
    plt.plot(px, py, 'D', color = 'red')
    print ('The function evaluation times is: {}'.format(len(py)))
    plt.plot(px, py, color = 'blue')
    plt.title('Cost Function $y = f(x)$') # Latex Type Equation.
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()
    result = scipy_minimize(cost_function, x0, method='BFGS', options={'disp':True})
    print ('The scipy method founded x is: {}'.format(result.x))
    print ('The correspond cost function value is: {}'.format(cost_function(result.x)))

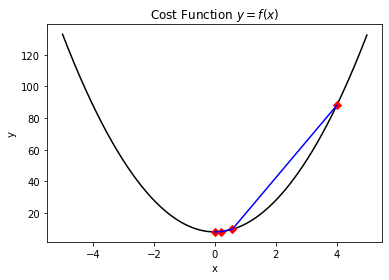
这里简单对代码中的参数作一个解释：DELTA是计算梯度值时所采用的步长，EPSILON是精度要求，MAX_STEPS是最大迭代次数(避免因为达不到自洽收敛条件而陷入死循环)，GAMMA是学习率(在其他的一些基于梯度的算法中可能会采用自适应的学习率或者逐步下降的学习率来达到更好的收敛效果)。该简单案例得到的结果如下所示：

The last value of y is: 8.00000000000125
The last value of x is: -5.000249774511634e-07
The function evaluation times is: 4

Optimization terminated successfully.
         Current function value: 8.000000
         Iterations: 3
         Function evaluations: 8
         Gradient evaluations: 4
The scipy method founded x is: [-9.56720569e-09]
The correspond cost function value is: [8.]

这里我们可以看到，自定义的函数迭代次数4次要小于通用库中所实现的8次函数估计。这里由于名称的定义有可能导致迭代次数和函数估计次数被混淆，一般基于梯度的算法是多次函数估计后才会迭代一次，而有些非梯度的优化算法如COBYLA等，则是每计算一次代价函数就代表迭代一次，这里我们能够简单从数量上理解即可。

补充测试案例

在上面二次函数的优化成功之后，我们可以尝试一些其他形式的函数的优化效果，如本次使用的正弦函数：

from scipy.optimize import minimize as scipy_minimize
from tqdm import trange
import matplotlib.pyplot as plt
import numpy as np

DELTA = 1e-06
EPSILON = 1e-06
MAX_STEPS = 100
GAMMA = 2
MOMENTUM =0.9

def cost_function(x):
    return np.sin(x)

def gradient(x, func):
    return (func(x + DELTA) - func(x)) / DELTA

def next_x(x, func, iterations, v):
    _tmpx = x - GAMMA  * gradient(x, func) / (iterations + 1) + MOMENTUM * v
    return _tmpx if cost_function(_tmpx) < cost_function(x) and gradient(_tmpx, func) * gradient(x, func) >= 0 else x

def minimize(x0, func):
    _x1 = x0
    _y1 = func(_x1)
    plot_x = [_x1]
    plot_y = [_y1]
    v = 0
    for i in trange(MAX_STEPS):
        _x = next_x(_x1, func, i, v)
        _y = func(_x)
        v = _x - _x1
        if v == 0:
            continue
        if abs(_y - _y1) <= EPSILON:
            print ('The minimum value {} founded :)'.format(_y))
            print ('The correspond x value is: {}'.format(_x))
            print ('The iteration times is: {}'.format(i))
            return _y, _x, plot_y, plot_x
        _x1 = _x
        _y1 = _y
        plot_x.append(_x1)
        plot_y.append(_y1)
    print ('The last value of y is: {}'.format(_y))
    print ('The last value of x is: {}'.format(_x))
    return _y, _x, plot_y, plot_x

if __name__ == '__main__':
    x0 = 1.4
    yt, xt, py, px = minimize(x0, cost_function)
    plt.figure()
    x = [i / 100 - 5 for i in range(1000)]
    y = [cost_function(i) for i in x]
    plt.plot(x, y, color = 'black')
    plt.plot(px, py, 'D', color = 'red')
    print ('The function evaluation times is: {}'.format(len(py)))
    plt.plot(px, py, color = 'blue')
    plt.title('Cost Function $y = f(x)$') # Latex Type Equation.
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()
    result = scipy_minimize(cost_function, x0, method='BFGS', options={'disp':True})
    print ('The scipy method founded x is: {}'.format(result.x))
    print ('The correspond cost function value is: {}'.format(cost_function(result.x)))

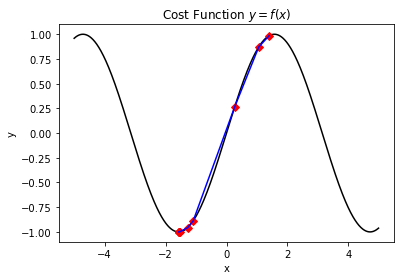
其执行效果如下：

The minimum value -0.9999986210818882 founded :)
The correspond x value is: -1.569135653179335
The iteration times is: 14
The function evaluation times is: 11

Optimization terminated successfully.
         Current function value: -1.000000
         Iterations: 2
         Function evaluations: 16
         Gradient evaluations: 8
The scipy method founded x is: [-1.57079993]
The correspond cost function value is: [-1.]

在该测试案例中，通过合理的参数配置，我们同样可以找到比标准库数量更少的迭代次数。其实在大部分的黑盒优化的情况下，我们并不能事先就计算好函数对应的轮廓，也无从获取相关信息，甚至函数运算本身也是一个复杂性较高的计算工作。因此，对于迭代次数或者函数值估计的次数的优化，也是一个值得研究的方向。

总结概要

梯度下降法是众多优化算法的基础形式，而一众优化算法在机器学习、神经网络训练以及变分量子算法实现的过程中都发挥着巨大的作用。通过了解基本的梯度下降函数的实现原理，可以为我们带来一些优化的思路，后续也会补充一些梯度下降函数的变种形式。可能有读者注意到，本文中的实际的函数值估计次数要大于结果中所展现的函数值估计次数。这个观点是对的，但是这里我们可以通过后续会单独讲解的lru缓存法来进行处理，这使得同样的参数输入下对于一个函数的访问可以几乎不需要时间，因此对于一个函数值的估计次数，其实仅跟最后得到的不同函数值的数量有关，中间存在大量的简并。

版权声明

本文首发链接为：https://www.cnblogs.com/dechinphy/p/gradient.html
作者ID：DechinPhy
更多原著文章请参考：https://www.cnblogs.com/dechinphy/