Python实现多维傅里叶变换

技术背景

在前面一篇文章中，我们介绍了一维离散傅里叶变换和快速傅里叶变换的基本原理和简单的代码实现。本文补充一个多维傅里叶变换的场景，以及简单的Python实现。

二维傅里叶变换

首先回顾一下上一篇文章中介绍的一维傅里叶变换与逆傅里叶变换的形式：

\[y_k=\sum_{n=0}^{N-1}x_ne^{-j\frac{2\pi nk}{N}},0\leq k\leq N-1\\ x_n=\frac{1}{N}\sum_{k=0}^{N-1}y_ke^{j\frac{2\pi nk}{N}},0\leq n\leq N-1 \]

那么首先我们通过前面一篇文章中的简单DFT实现来理解一下一维傅里叶变换的物理图像：

import numpy as np

def dft(x):
    y = np.zeros_like(x, dtype=np.complex64)
    N = x.shape[0]
    for k in range(N):
        y[k] = np.sum(x * np.exp(-1j*2*np.pi*k*np.arange(N)/N))
    return y

我们先不讨论时域和频域的概念，这里只有输入x和输出y，那么每一点的y的数据，都是通过一系列的参数矢量与x矢量的内积。换句话说，x上的每一个数据点都对y的每一个数据点有贡献，这个贡献的大小通过傅里叶变换的参数来给定：

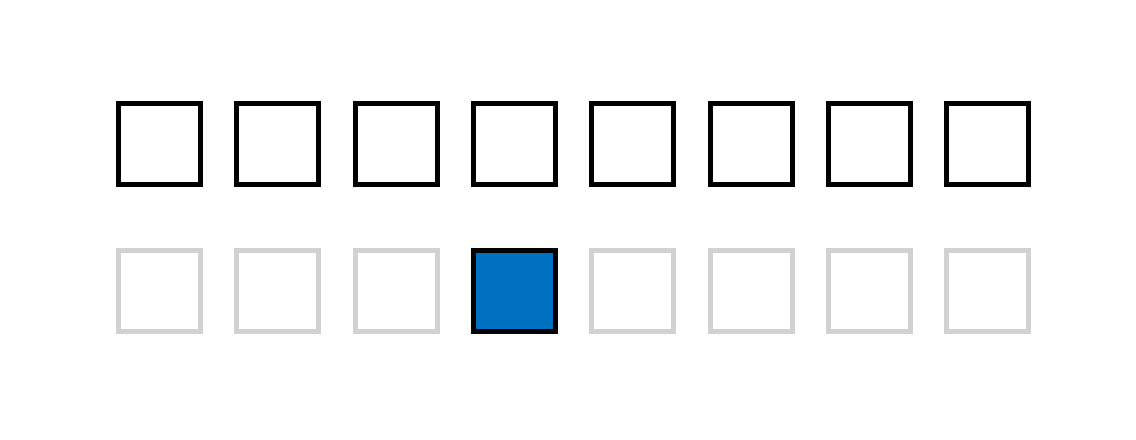
那么高维傅里叶变换，其实就是按顺序在每个维度上做内积：

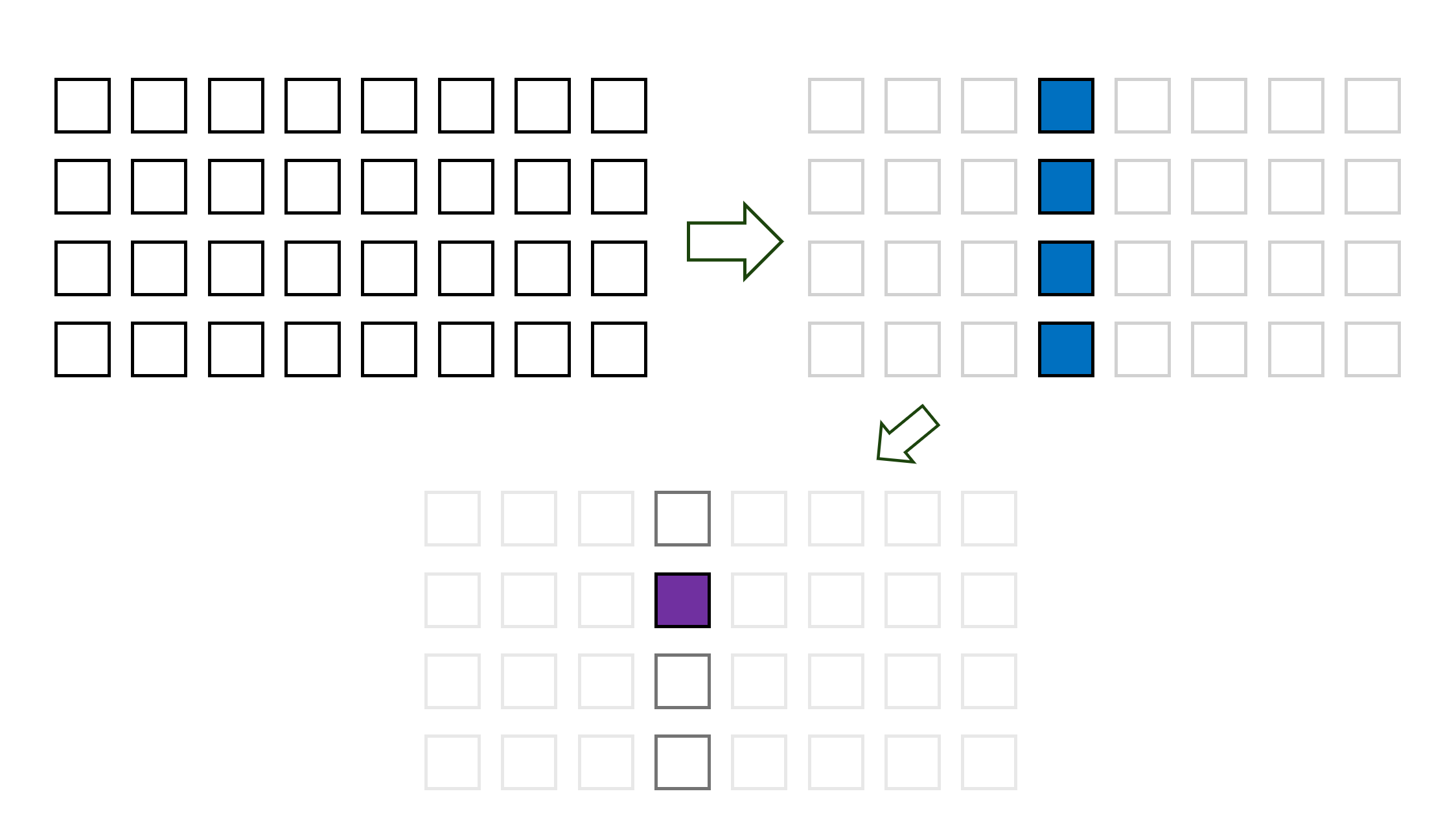
对应的代数形式为：

\[y_{k_1,k_2}=\sum_{n_2=0}^{D-1}e^{-j\frac{2\pi n_2k_2}{D}}\sum_{n_1=0}^{N-1}x_{n_1,n_2}e^{-j\frac{2\pi n_1k_1}{N}},0\leq k_1,k_2\leq N-1\\ x_{n_1,n_2}=\frac{1}{D}\sum_{k_2=0}^{D-1}e^{j\frac{2\pi n_2k_2}{D}}\frac{1}{N}\sum_{k_1=0}^{N-1}y_{k_1,k_2}e^{j\frac{2\pi n_1k_1}{N}},0\leq n_1,n_2\leq N-1 \]

至于更高维度的傅里叶变换，就是继续增加求和的维度。也有一种常见的写法是采用归一化的矢量内积形式：

\[y_{\vec{k}}=\sum_{\vec{n}}e^{-2j\pi\vec{k}\cdot\vec{n}}x_{\vec{n}} \]

至于FFT的形式，只是对其中的特定维度进行分解，这里不做更多分析，可以直接看一下多维DFT的一个简单实现。

Python代码实现

这里使用Python实现一个最简单的二维傅里叶变换和逆傅里叶变换，没有经过任何的优化：

import numpy as np

def dftn(x):
    y = np.zeros_like(x, dtype=np.complex64)
    N = x.shape[0]
    D = x.shape[1]
    for k1 in range(N):
        for k2 in range(D):
            for n1 in range(N):
                for n2 in range(D):
                    y[k1][k2] += np.exp(-2j*np.pi*(k2*n2)/D)* np.exp(-2j*np.pi*(k1*n1)/N) * x[n1][n2]
    return y

def idftn(y):
    x = np.zeros_like(y, dtype=np.complex64)
    N = y.shape[0]
    D = y.shape[1]
    for n1 in range(N):
        for n2 in range(D):
            for k1 in range(N):
                for k2 in range(D):
                    x[n1][n2] += np.exp(2j*np.pi*(k2*n2)/D) * np.exp(2j*np.pi*(k1*n1)/N) * y[k1][k2] / N / D
    return x

N = 16
x = np.random.random((N, 3)).astype(np.float32)
y0 = dftn(x)
y1 = np.fft.fft2(x)
x0 = idftn(y1)
x1 = np.fft.ifft2(y0)
print (np.allclose(y0, y1))
print (np.allclose(x0, x1))
# True
# True

经过和numpy中实现方式的对比，两边结果一致。

总结概要

继前一篇文章中的一维傅里叶变换，本文介绍了多维傅里叶变换的物理图像和基本原理，并附带了Python简单实现。并将Python的计算结果与Numpy中已经实现的二维傅里叶变换的结果进行对比。

版权声明

本文首发链接为：https://www.cnblogs.com/dechinphy/p/fftn.html

作者ID：DechinPhy

更多原著文章：https://www.cnblogs.com/dechinphy/

请博主喝咖啡：https://www.cnblogs.com/dechinphy/gallery/image/379634.html