Numpy本征值求解

技术背景

Numpy是一个Python库中最经常被用于执行计算任务的一个包，得益于其相比默认列表的高性能表现，以及易用性和可靠性，深受广大Python开发者的喜爱。这里介绍的是使用Numpy计算矩阵本征值和本征矩阵的方法。

求解问题

本征问题是求解形如：\(\mathbf{A}\mathbf{v}=\lambda\mathbf{v}\)的方程，其中\(\mathbf{A}\)为已知矩阵，\(\mathbf{v}\)为其中一个本征向量，\(\lambda\)是其中一个本征值。求解这个本征方程，就是找到所有符合条件的本征向量和对应的本征值。如果把所有的本征向量用一个本征矩阵\(\mathbf{V}\)来表示，那么就得到了一个特征值分解（EVD）：

\[\mathbf{A} = \mathbf{V}\Sigma\mathbf{V}^{-1} \]

其中\(\Sigma\)是由所有的特征值\(\lambda\)组成的对角矩阵。该形式的分解与另外一种SVD奇异值分解，在各种数据降维和稀疏化中经常会用到。

代码示例

这里用IPython做一个简单的功能演示：

In [1]: import numpy as np

In [2]: x = np.random.random((3,3)) # 生成一个随机3x3矩阵

In [3]: x
Out[3]: 
array([[0.85976743, 0.98470964, 0.93286037],
       [0.4988825 , 0.36451386, 0.68983566],
       [0.01818865, 0.27647914, 0.86250282]])

In [4]: vals, vecs = np.linalg.eig(x) # 求解本征值和本征矩阵

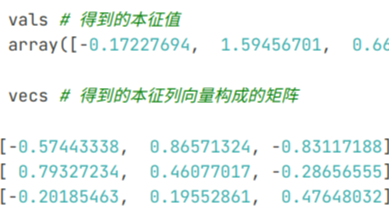
In [5]: vals # 得到的本征值
Out[5]: array([-0.17227694,  1.59456701,  0.66449404])

In [6]: vecs # 得到的本征列向量构成的矩阵
Out[6]: 
array([[-0.57443338,  0.86571324, -0.83117188],
       [ 0.79327234,  0.46077017, -0.28656555],
       [-0.20185463,  0.19552861,  0.47648032]])

In [7]: np.allclose(vecs @ np.diag(vals) @ np.linalg.inv(vecs), x) # 测试本征值分解EVD
Out[7]: True

In [13]: np.allclose(x @ vecs[:, 0], vecs[:, 0] * vals[0]) # 测试本征向量
Out[13]: True

In [14]: np.allclose(x @ vecs[:, 1], vecs[:, 1] * vals[1]) # 测试本征向量
Out[14]: True

In [15]: np.allclose(x @ vecs[:, 2], vecs[:, 2] * vals[2]) # 测试本征向量
Out[15]: True

可以看到，EVD分解还原之后的矩阵跟原矩阵是保持一致的。这里逆矩阵的运算，也是用到了numpy的另外一个操作：矩阵求逆函数numpy.linalg.inv。