三种二叉树遍历的非递归算法
本文章参考了:https://blog.csdn.net/zhangxiangdavaid/article/details/37115355 的总结;相对原文,力求更加简要的对三种二叉树遍历的非递归算法进行归纳
一、二叉树中序遍历的非递归算法 - LNR
既然是非递归算法,我们自然要借助栈。那么关键就是确定什么时候进行入栈,访问、出栈这几个动作。
整个中序递归遍历的思路理解起来并不难,他和我们手动用 LNR 写出中序遍历的思路很相近:
入栈:结点非空时,结点进栈,往左走;
访问:栈非空,每出栈一个结点,便访问并往右走;

当每次向左走到空叶结点时,有上图两种情况;但当我们使用空叶子结点时,左边情况是右边情况的一种,两者可以统一处理,即:
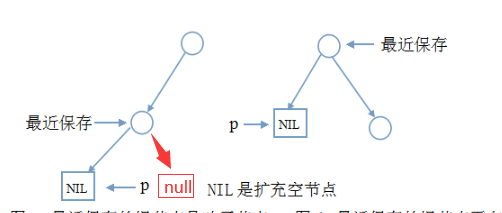
所以中序遍历的非递归代码很简洁:
//中序遍历 void InOrderWithoutRecursion2(BTNode* root) { //空树 if (root == NULL) return; //树非空 BTNode* p = root; stack<BTNode*> s; while (!s.empty() || p) { if (p) { s.push(p); p = p->lchild; } else { p = s.top(); s.pop(); cout << setw(4) << p->data; //打印在出栈时 p = p->rchild; } }
二、二叉树先序遍历的非递归算法 - NLR
理解了一之后,再来看先序的非递归算法就很好理解了。两者的区别,只是打印位置的提前,我们脑海中对一棵二叉树的搜索过程是一样的。直接给上代码:
//前序遍历 void PreOrderWithoutRecursion2(BTNode* root) { if (root == NULL) return; BTNode* p = root; stack<BTNode*> s; while (!s.empty() || p) { if (p) { cout << setw(4) << p->data;//打印在向左搜寻时 s.push(p); p = p->lchild; } else { p = s.top(); s.pop(); p = p->rchild; } } cout << endl;
三、二叉树后续遍历非递归算法 LRN
非递归后续遍历算法是3者中最难的,但实际上还是一样,重在理解:入栈,访问、出栈的操作规律
关键是理解:访问一个结点发生在,该节点无右孩子 或者 有右孩子但右孩子刚刚访问
代码的逻辑如下:
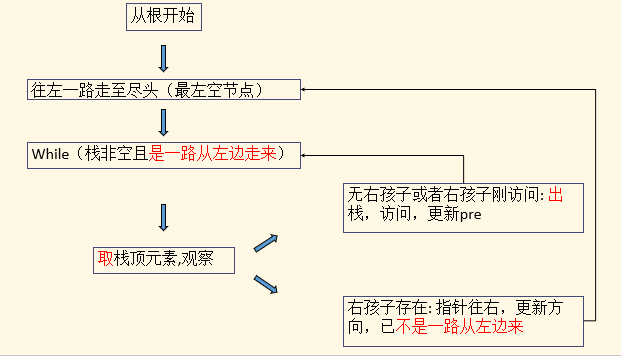
代码:(来自https://www.cnblogs.com/Dawn-bin/p/9844442.html )
flag = 1表示是一路从左遍历至空节点;
1 Status PostOrderTraverse(BiTree T){ 2 BiTree p = T, S[100], pre; 3 int top = 0, flag = 1; 4 if(p) 5 do{ 6 while(p){ 7 S[top++] = p; 8 p = p->lchild; 9 } 10 // p所有左节点入栈 11 flag = 1; 12 13 while(top != 0 && flag == 1){ 14 p = S[top-1]; 15 if(p->rchild == pre || p->rchild == NULL){ 16 //右孩子不存在或右孩子已访问 17 top--; 18 printf("%c ", p->data); 19 pre = p; 20 //指向被访问节点 21 } 22 else{ 23 //继续遍历右子树 24 p = p->rchild; 25 flag = 0; 26 } 27 } 28 }while(top != 0); 29 return OK; 30 }//PostOrderTraverse
该算法的特点是,栈中所保存的是出栈结点至根的所有祖先结点,利用这点后续非递归遍历有很多应该,比如:
(1).输出某个叶子结点的所有祖先
(2).输出根结点到所有叶子结点的路径
(3).如果二叉树结点的值是数值,那么求每条路径上值之和



 浙公网安备 33010602011771号
浙公网安备 33010602011771号