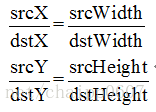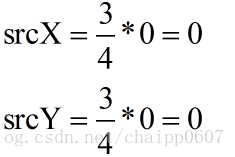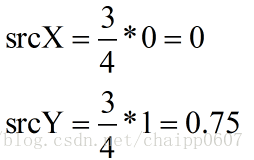c#数字图像处理(十)图像缩放
图像几何变换(缩放、旋转)中的常用的插值算法
在图像几何变换的过程中,常用的插值方法有最邻近插值(近邻取样法)、双线性内插值和三次卷积法。
最邻近插值:
这是一种最为简单的插值方法,在图像中最小的单位就是单个像素,但是在旋转个缩放的过程中如果出现了小数,那么就对这个浮点坐标进行简单的取整,得到一个整数型坐标,这个整数型坐标对应的像素值就是目标像素的像素值。取整的方式就是:取浮点坐标最邻近的左上角的整数点。
举个例子:
3*3的灰度图像,其每一个像素点的灰度如下所示
我们要通过缩放,将它变成一个4*4的图像,那么其实相当于放大了4/3倍,从这个倍数我们可以得到这样的比例关系:
根据公式可以计算出目标图像中的(0,0)坐标与原图像中对应的坐标为(0,0)
(由于分母不能为0,所以我们将公式改写)
然后我们就可以确定出目标图像中(0,0)坐标的像素灰度了,就是234。
然后我们在确定目标图像中的(0,1)坐标与原图像中对应的坐标,同样套用公式:
我们发现,这里出现了小数,也就是说它对应的原图像的坐标是(0,0.75),显示这是错误的,如果我们不考虑亚像素情况,那么一个像素单位就是图像中最小的单位了,那么按照最临近插值算法,我们找到距离0.75最近的最近的整数,也就是1,那么对应的原图的坐标也就是(0,1),像素灰度为67。
双线性内插值:
对于一个目的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v),其中i、j均为非负整数,u、v为[0,1)区间的浮点数,则这个像素得值 f(i+u,j+v) 可由原图像中坐标为 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定,即:
f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1)
其中f(i,j)表示源图像(i,j)处的的像素值。
那么还是上面的例子,目标图像中(0,1)对应的原图像浮点坐标是(0,0.75),套用上面的公式这个坐标可以写成(0+0,0+0.75),其中i=0,j=0,u=0,v=0.75
我们套用公式看一下它最后的灰度
f(i+u,j+v) = 0.25*f(0,0)+0.75*f(0,1)=0.25*234+0.75*67
约等于108
这就是双线性内插值法。双线性内插值法计算量大,但缩放后图像质量高,不会出现像素值不连续的的情况。由于双线性插值具有低通滤波器的性质,使高频分量受损,所以可能会使图像轮廓在一定程度上变得模糊。
三次卷积法:
其实这个方法在好像有很多叫法,它在OpenCV中被命名为INTER_CUBIC,就是立方(三次)的意思,现在我把它和三次卷积法认为是同一种算法,引用一个帖子里面的话:
全称双立方(三次)卷积插值。
代码或许有不同写法,实现方式就一种
该算法是对函数 sin x / x 的一种近似,也就是说 原图像对目标图像的影响
等于 目标点对应于原图像点周围 x距离的点,按照 sin x / x 比例 的加权平均 。
这里x代表,周围得点跟目标点, x或者 y 轴 对应于原图的相对位置。
sin x / x 是归一化了的,实际应用的是近似公式
f(i+u,j+v) = [A] * [B] * [C]
[A]=[ S(u + 1) S(u + 0) S(u - 1) S(u - 2) ]
┏ f(i-1, j-1) f(i-1, j+0) f(i-1, j+1) f(i-1, j+2) ┓
[B]=┃ f(i+0, j-1) f(i+0, j+0) f(i+0, j+1) f(i+0, j+2) ┃
┃ f(i+1, j-1) f(i+1, j+0) f(i+1, j+1) f(i+1, j+2) ┃
┗ f(i+2, j-1) f(i+2, j+0) f(i+2, j+1) f(i+2, j+2) ┛
┏ S(v + 1) ┓
[C]=┃ S(v + 0) ┃
┃ S(v - 1) ┃
┗ S(v - 2) ┛
┏ 1-2*Abs(x)^2+Abs(x)^3 , 0<=Abs(x)<1 ┓
S(x)={ 4-8*Abs(x)+5*Abs(x)^2-Abs(x)^3 , 1<=Abs(x)<2 ┃
┗ 0 , Abs(x)>=2 ┛
S(x)是对 Sin(x*Pi)/x 的逼近(Pi是圆周率——π)
public enum ZoomType { NearestNeighborInterpolation , BilinearInterpolation } /// <summary> /// 图像缩放 /// </summary> /// <param name="srcBmp">原始图像</param> /// <param name="width">目标图像宽度</param> /// <param name="height">目标图像高度</param> /// <param name="dstBmp">目标图像</param> /// <param name="GetNearOrBil">缩放选用的算法</param> /// <returns>处理成功 true 失败 false</returns> public static bool Zoom(Bitmap srcBmp, double ratioW, double ratioH, out Bitmap dstBmp, ZoomType zoomType) {//ZoomType为自定义的枚举类型 if (srcBmp == null) { dstBmp = null; return false; } //若缩放大小与原图一样,则返回原图不做处理 if ((ratioW == 1.0) && ratioH == 1.0) { dstBmp = new Bitmap(srcBmp); return true; } //计算缩放高宽 double height = ratioH * (double)srcBmp.Height; double width = ratioW * (double)srcBmp.Width; dstBmp = new Bitmap((int)width, (int)height); BitmapData srcBmpData = srcBmp.LockBits(new Rectangle(0, 0, srcBmp.Width, srcBmp.Height), ImageLockMode.ReadWrite, PixelFormat.Format24bppRgb); BitmapData dstBmpData = dstBmp.LockBits(new Rectangle(0, 0, dstBmp.Width, dstBmp.Height), ImageLockMode.ReadWrite, PixelFormat.Format24bppRgb); unsafe { byte* srcPtr = null; byte* dstPtr = null; int srcI = 0; int srcJ = 0; double srcdI = 0; double srcdJ = 0; double a = 0; double b = 0; double F1 = 0;//横向插值所得数值 double F2 = 0;//纵向插值所得数值 if (zoomType==ZoomType.NearestNeighborInterpolation) {//邻近插值法 for (int i = 0; i < dstBmp.Height; i++) { srcI = (int)(i / ratioH);//srcI是此时的i对应的原图像的高 srcPtr = (byte*)srcBmpData.Scan0 + srcI * srcBmpData.Stride; dstPtr = (byte*)dstBmpData.Scan0 + i * dstBmpData.Stride; for (int j = 0; j < dstBmp.Width; j++) { dstPtr[j * 3] = srcPtr[(int)(j / ratioW) * 3];//j / ratioW求出此时j对应的原图像的宽 dstPtr[j * 3 + 1] = srcPtr[(int)(j / ratioW) * 3 + 1]; dstPtr[j * 3 + 2] = srcPtr[(int)(j / ratioW) * 3 + 2]; } } } else if (zoomType==ZoomType.BilinearInterpolation) {//双线性插值法 byte* srcPtrNext = null; for (int i = 0; i < dstBmp.Height; i++) { srcdI = i / ratioH; srcI = (int)srcdI;//当前行对应原始图像的行数 srcPtr = (byte*)srcBmpData.Scan0 + srcI * srcBmpData.Stride;//指原始图像的当前行 srcPtrNext = (byte*)srcBmpData.Scan0 + (srcI + 1) * srcBmpData.Stride;//指向原始图像的下一行 dstPtr = (byte*)dstBmpData.Scan0 + i * dstBmpData.Stride;//指向当前图像的当前行 for (int j = 0; j < dstBmp.Width; j++) { srcdJ = j / ratioW; srcJ = (int)srcdJ;//指向原始图像的列 if (srcdJ < 1 || srcdJ > srcBmp.Width - 1 || srcdI < 1 || srcdI > srcBmp.Height - 1) {//避免溢出(也可使用循环延拓) dstPtr[j * 3] = 255; dstPtr[j * 3 + 1] = 255; dstPtr[j * 3 + 2] = 255; continue; } a = srcdI - srcI;//计算插入的像素与原始像素距离(决定相邻像素的灰度所占的比例) b = srcdJ - srcJ; for (int k = 0; k < 3; k++) {//插值 公式:f(i+p,j+q)=(1-p)(1-q)f(i,j)+(1-p)qf(i,j+1)+p(1-q)f(i+1,j)+pqf(i+1, j + 1) F1 = (1 - b) * srcPtr[srcJ * 3 + k] + b * srcPtr[(srcJ + 1) * 3 + k]; F2 = (1 - b) * srcPtrNext[srcJ * 3 + k] + b * srcPtrNext[(srcJ + 1) * 3 + k]; dstPtr[j * 3 + k] = (byte)((1 - a) * F1 + a * F2); } } } } } srcBmp.UnlockBits(srcBmpData); dstBmp.UnlockBits(dstBmpData); return true; }

最近邻插值放大5倍:

双线性插值放大5倍: