Fast and easy high resolution fractals with a pixel shader
Fast and easy high resolution fractals with a pixel shader
by John Tsiombikas (Nuclear / Mindlapse)
nuclear@siggraph.org
Table of Contents
- Programmable Graphics Hardware
- Calculating Fractals on the GPU
- The Mandelbrot Fractal
- The Julia Fractal
- Example Programs
- Relevant Links
The beauty of fractals like the mandelbrot or julia sets, comes from the fact that the evaluation of an extremely simple function, produces such an infinite amount of complex detail. However, even a fast computer has a hard time to perform the calculations in realtime for any reasonable number of iterations, so, traditionally, realtime fractal programs had to perform a number of precalculations, like calculating every n-th frame and interpolating the in-between or calculating the most important areas and interpolating the rest, in order to achieve real-time framerates.
Programmable Graphics Hardware
Not too many years ago, graphics hardware able to fill polygons, perform 3D transformations, and lighting calculations was the prerogative of the few lucky souls, programming on expensive SGI workstations. However, for a few years now, the explosion of the PC gaming market led to the comoditization of extremely powerful graphics co-processors, which are nowadays taken for granted by the majority of PC users.
The latest crop of such graphics processing units, let the programmer upload and run a custom program that overrides the default vertex or pixel processing pipelines, thus providing a great deal of flexibility required to implement alternative illumination models, per pixel lighting, custom compositing, or any other weird effect the programmer might need.
Calculating Fractals on the GPU
The GPU is a parallel vector processor, and as such, it's extremly suitable for calculating mandelbrot or julia fractals which are extremely easy to parallelize, due to the mutual-independence of the calculations for each pixel. I.e. calculating the fractal for any given pixel, does not need any information about the calculation results of nearby pixels.
The process we have to follow, to calculate such a fractal in the GPU is very straightforward. We will have to write a simple pixel (aka fragment) shader that will performe the necessary calculations for each pixel of the fractal, and then make arrangements for this to be called for every pixel of the screen.
Setting up Everything with OpenGL
For a pixel shader to run, we have to render polygons after activating the shader, and for each pixel that needs to be drawn as a result of rendering any of these polygons, the shader is automatically run to calculate its final color.
In our case, since we want the fractal to cover the entire area of the screen, we will draw a rectangle covering the entire screen. This is very easy to do with OpenGL; with the default state of OpenGL, i.e all matrices set to identity, and the viewport set to (0, 0, xres, yres), all we need to do is draw a quad covering the area from (-1, -1) to (1, 1), as illustrated by the code snippet below:
| Drawing a full-screen quad |
|---|
| glBegin(GL_QUADS); glTexCoord2f(0, 0); glVertex2f(-1, -1); glTexCoord2f(1, 0); glVertex2f(1, -1); glTexCoord2f(1, 1); glVertex2f(1, 1); glTexCoord2f(0, 1); glVertex2f(-1, 1); glEnd(); |
Note that we also included texture coordinates, which will be needed later-on for our pixel shader.
In order to use our pixel shader we have to perform the following actions:
- Create a shader object with glCreateShaderObjectARB, pass the shader source to it with glShaderSourceARB, and compile it with glCompileShaderARB.
- Create a program object by calling glCreateProgramObjectARB, attach the shader with glAttachObjectARB and link the program with glLinkProgramARB.
- Finally we need to enable the GLSL program by calling: glUseProgramObjectARB and draw the fullscreen quad as described above.
I won't go into more details here, refer to the OpenGL 2.0 and GL Shading Language specifications and books (see relevant links at the end of this article).
The Mandelbrot Fractal
The mandelbrot set is a subset of the complex numbers. When visualized on the complex plane, it gives the familliar image often referred to as the "gingerbread man". The image to the right, is a direct plot of the mandelbrot set on the complex plane, black points are elements of the set, while white points are not. The membership of a complex number to the mandelbrot set is determined by evaluating the following recursive function: 
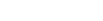. The mandelbrot set is defined as the set of complex number for which 
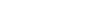. Of course we cannot evaluate the equation infinite times, so we have to settle for a big number for n instead. Also it can be proven that if at any point ||z|| becomes greater than 2, it will eventually go to infinity, so we can stop the evaluation based on that condition, and classify the number as not belonging to the set.
Coloring the Mandelbrot
A binary plot of the mandelbrot set obviously produces black & white images which are not all that nice. Thus it is customary to color the pixels outside of the mandelbrot set, based on the number of iterations it took to decide that the complex number under consideration is not part of the set (i.e. the number of iterations it took for its magnitude to grow bigger than 2). So, typically, we color everything in the set as black, and everything else by indexing a palette with the number of iterations.
The Mandelbrot Shader
First of all, to give the palette to the shader, we will make a 256x1 (1-dimensional) texture with the colors we want, and bind it before rendering. Just make sure you have disabled texture filtering (use GL_NEAREST). This palette texture is used for all the images throughout the article: 
.
| Mandelbrot GLSL Fragment Shader |
|---|
uniform sampler1D tex;
uniform vec2 center;
uniform float scale;
uniform int iter;
void main() {
vec2 z, c;
c.x = 1.3333 * (gl_TexCoord[0].x - 0.5) * scale - center.x;
c.y = (gl_TexCoord[0].y - 0.5) * scale - center.y;
int i;
z = c;
for(i=0; i<iter; i++) {
float x = (z.x * z.x - z.y * z.y) + c.x;
float y = (z.y * z.x + z.x * z.y) + c.y;
if((x * x + y * y) > 4.0) break;
z.x = x;
z.y = y;
}
gl_FragColor = texture1D(tex, (i == iter ? 0.0 : float(i)) / 100.0);
}
|
That's all! Four uniforms are passed from the OpenGL program, tex is the palette texture, center is the center of the screen in the complex plane, scale is a factor which is used to calculate the extends of the window in the complex plane, and iter is the number of maximum iterations to perform. Note that gl_FragCoord could be used instead of the texture coordinates of the quad, but this way the quad can be situated and oriented arbitrarily in 3D space and the effect will still work as expected.
The Julia Fractal
The Julia set, is very similar to the mandelbrot set, in fact there is a direct connection between them. For every point in the complex plane, a corresponding julia set can be generated; the julia set is connected for points belonging to the mandelbrot set, and disconnected otherwise.
The algorithm is again very simple, using a complex number c as a "seed", we determine which of the complex numbers in the plane escape to infinity after a sufficient number of iterations, of the same recursive formula as the mandelbrot set: .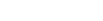
The Julia Shader
| Julia GLSL Fragment Shader |
|---|
uniform sampler1D tex;
uniform vec2 c;
uniform int iter;
void main() {
vec2 z;
z.x = 3.0 * (gl_TexCoord[0].x - 0.5);
z.y = 2.0 * (gl_TexCoord[0].y - 0.5);
int i;
for(i=0; i<iter; i++) {
float x = (z.x * z.x - z.y * z.y) + c.x;
float y = (z.y * z.x + z.x * z.y) + c.y;
if((x * x + y * y) > 4.0) break;
z.x = x;
z.y = y;
}
gl_FragColor = texture1D(tex, (i == iter ? 0.0 : float(i)) / 100.0);
}
|
Again, the shader is pretty simple, we have the texture with th palette, tex, the seed, c, and the number of iterations, iter, passed by the OpenGL program as uniforms. z starts from the current complex number (position of the pixel in the plane), and we follow its orbit until it grows beyond 2, and thus is guaranteed to go to infinity, or we run out of iterations. Then we proceed to color it as usual, by using the number of iterations as an index in the palette texture.
Example Programs
Download example: sdr_fract.tar.gz (4.7k)
These are the two programs, implementing a mandelbrot zoomer, and a julia explorer, in the GPU, as described by this article. A UNIX makefile that builds both of them is provided in the tarball, but the programs should be able to compile and run on any OS, the only dependency being glut. Also, you will probably going to need a ps3.0 graphics card like the Geforce 6x00 or the Radeon Xx00.
Consider the code as public domain, use it as you see fit.
