Longest Common Subsequence (LCS)

Longest Common Subsequence (LCS). The following are some instances.

a)  X: xzyzzyx   Y: zxyyzxz

b)  X:MAEEEVAKLEKHLMLLRQEYVKLQKKLAETEKRCALLAAQANKESSSESFISRLLAIVAD              

Y:MAEEEVAKLEKHLMLLRQEYVKLQKKLAETEKRCTLLAAQANKENSNESFISRLLAIVAG

 

思路：

子序列是一个字符串S去掉零个或者多个字符后所剩下的字符串就叫做子序列。

最长公共子序列的意思就是寻找两个给定字符串的的子序列，该子序列在两个字符串中以相同的次序出现，但是不一定是连续的。

应用动态规划方法:

• 1.刻画最长公共子序列的特征
• 2.一个递归解
• 3.计算LCS的长度
• 4.构造LCS

 

步骤1:特征分析

设X=“x0，x1，…，xm”，Y=“y0，y1，…，yn”，且Z=“z0，z1，…，zk”为它们的最长公共子序列。不难证明有以下性质：

       如果xm=yn，则zk=xm=yn，且“z0，z1，…，z(k-1)”是“x0，x1，…，x(m-1)”和“y0，y1，…，y(n-1)”的一个最长公共子序列；

       如果xm!=yn，则若zk!=xm，蕴涵“z0，z1，…，zk”是“x0，x1，…，x(m-1)”和“y0，y1，…，yn”的一个最长公共子序列；

　　 如果xm!=yn，则若zk!=yn，蕴涵“z0，z1，…，zk”是“x0，x1，…，xm”和“y0，y1，…，y(n-1)”的一个最长公共子序列。

步骤2:递归公式

与矩阵链乘法相似，设计LCS问题的递归算法首先要建立最优解的递归式。我们用c[i,j]表示Xi和Yi的LCS长度。如果i=0或j=0，即一个序列长度为0，那么LCS的长度为0。根据LCS问题的最优子结构性质，可得如下公式：

 

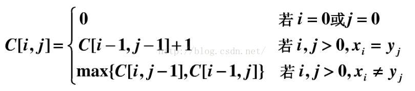
步骤3:计算LCS的长度

动态规划法自底向上计算LCS的长度

步骤4:构造LCS

public class Q2_LC_Subsequence {
    public static String X1="xzyzzyx";
    public static String Y1="zxyyzxz";
    public static String X2="MAEEEVAKLEKHLMLLRQEYVKLQKKLAETEKRCALLAAQANKESSSESFISRLLAIVAD";
    public static String Y2="MAEEEVAKLEKHLMLLRQEYVKLQKKLAETEKRCTLLAAQANKENSNESFISRLLAIVAG";
    public static void LCS_length(String X,String Y)
    {
        int m = X.length();
        int n = Y.length();
        char[] Xc = X.toCharArray();
        char[] Yc = Y.toCharArray();
        int[][] c = new int[m+1][n+1];
        int[][] b = new int[m+1][n+1];
        int i,j;

        for(i=0;i<=m;i++)
        {
            for(j=0;j<=n;j++)
            {
                if (i==0||j==0){
                c[i][j] = 0;
                b[i][j] = 0;
                }else if(Xc[i-1]==Yc[j-1])
                {
                    c[i][j] = c[i-1][j-1] + 1;
                    b[i][j] = 1;
                }else if(c[i-1][j]>=c[i][j-1])
                {
                    c[i][j] = c[i-1][j];
                    b[i][j] = 2;
                }else
                {
                    c[i][j] = c[i][j-1];
                    b[i][j] = 3;
                }
            }
        }
/*
        for(i=0;i<=m;i++)
        {
            for(j=0;j<=n;j++)
            {
                System.out.print(c[i][j]);
                System.out.print(' ');
            }
            System.out.println();
        }
        */
/*
        for(i=0;i<=m;i++)
        {
            for(j=0;j<=n;j++)
            {
                System.out.print(b[i][j]);
                System.out.print(' ');
            }
            System.out.println();
        }
        */
        Print_LCS(b,X,X.length(),Y.length());
    }

    public static void Print_LCS(int[][] b, String X, int i, int j){
        char[] Xc = X.toCharArray();
        if(i == 0 || j == 0)
        return ;
        if(b[i][j] == 1)
        {
            Print_LCS(b,X,i-1,j-1);
            System.out.print(Xc[i-1]);
            //System.out.print(' ');
        }else if(b[i][j] == 2)
        {
            Print_LCS(b,X,i-1,j);
        }else
        {
            Print_LCS(b,X,i,j-1);
        }
    }

    public static void main(String[] args)
    {
        LCS_length(X1,Y1);
        System.out.println();
        LCS_length(X2,Y2);
    }
}