经典排序算法 -----冒泡排序,插入排序,快速排序,归并排序,堆排序
排序算法


#include <iostream> #include <algorithm> using namespace std; void bubblesort(int a[],int len ) { for(int i = 0; i<len;++i) for(int j = i+1; j<len;++j) if(a[i]>a[j]) swap(a[i],a[j]); } int main() { int a[]={2,8,3,5,4,6,7,1,0}; int len = sizeof(a)/sizeof(int); bubblesort(a, len); for(int i =0; i<len;i++) cout<<a[i]<<" "; cout<<endl; }


#include <iostream> using namespace std; void InsertSort( int a[], int length) { for(int i =1; i<length;i++) { int temp = a[i];// copy it first int j = i-1; for(;j>=0 && temp<a[j];j--) // unsorted region;(0~(i-1) is sorted) a[j+1] = a[j]; // move back elements to empty a right position a[j+1] = temp; // place it to the right position } } int main() { int a[] = {3,4,7,8,9,0,2,1,10,5,6}; int length = sizeof(a)/sizeof(int); InsertSort(a,length); for(int i =0; i<length;i++) cout<<a[i]<<" "; cout<<endl; return 0; }
它采用了一种分治的策略,通常称其为分治法(Divide-and-ConquerMethod)。
该方法的基本思想是:
1.先从数列中取出一个数作为基准数。
2.分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
3.再对左右区间重复第二步,直到各区间只有一个数。
虽然快速排序称为分治法,但分治法这三个字显然无法很好的概括快速排序的全部步骤。因此我的对快速排序作了进一步的说明:挖坑填数+分治法:
先来看实例吧,定义下面再给出(最好能用自己的话来总结定义,这样对实现代码会有帮助)。
以一个数组作为示例,取区间第一个数为基准数
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
72 |
6 |
57 |
88 |
60 |
42 |
83 |
73 |
48 |
85 |
初始时,i = 0; j = 9; X = a[i] = 72
由于已经将a[0]中的数保存到X中,可以理解成在数组a[0]上挖了个坑,可以将其它数据填充到这来。
从j开始向前找一个比X小或等于X的数。当j=8,符合条件,将a[8]挖出再填到上一个坑a[0]中。a[0]=a[8]; i++; 这样一个坑a[0]就被搞定了,但又形成了一个新坑a[8],这怎么办了?简单,再找数字来填a[8]这个坑。这次从i开始向后找一个大于X的数,当i=3,符合条件,将a[3]挖出再填到上一个坑中a[8]=a[3];
数组变为:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
48 |
6 |
57 |
88 |
60 |
42 |
83 |
73 |
88 |
85 |
i = 3; j = 7; X=72
再重复上面的步骤,先从后向前找,再从前向后找。
从j开始向前找,当j=5,符合条件,将a[5]挖出填到上一个坑中,a[3] = a[5];
从i开始向后找,当i=5时,由于i==j退出。
此时,i = j = 5,而a[5]刚好又是上次挖的坑,因此将X填入a[5]。
数组变为:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
48 |
6 |
57 |
42 |
60 |
72 |
83 |
73 |
88 |
85 |
对挖坑填数进行总结
1.i =L; j = R; 将基准数挖出形成第一个坑a[i]。
2.j--由后向前找比它小的数,找到后挖出此数填前一个坑a[i]中。
3.i++由前向后找比它大的数,找到后也挖出此数填到前一个坑a[j]中。
using namespace std;
#include <iostream> using namespace std; void quicksort(int a[], int left, int right){ int first = left; int last = right; int key = a[left]; if(left>=right) return ; while(first<last){ while(first<last && a[last]>=key) last--; a[first] = a[last]; while(first<last && a[first]<key) first++; a[last]= a[first]; } a[first] = key; quicksort(a,left , first-1); quicksort(a,first+1,right); } int main() { int a[] = {8,2,6,1,4,3,5,7,0}; int len = sizeof(a)/sizeof(int); quicksort(a,0,len-1); for(int i =0; i<len;++i) cout<<a[i]<<" " ; cout<<endl; return 0; }
快速排序的效果图

void mergeTwo(int a[],int m, int b[],int n,int c[]){ int i ,j,k; i =j =k=0; while(i<m&&j<n) { if(a[i]<b[j]) c[k++] = a[i++]; else c[k++] =b[j++]; } while(i<m) c[k++]=a[i++]; while(j<n) c[k++]=b[j++]; }
(1)基本排序:归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
(2)实例:
#include <iostream> using namespace std; void mergearray(int a[], int first, int mid, int last, int temp[]) { int i = first, j = mid + 1; int m = mid, n = last; int k = 0; while (i <= m && j <= n) { if (a[i] <= a[j]) temp[k++] = a[i++]; else temp[k++] = a[j++]; } while (i <= m) temp[k++] = a[i++]; while (j <= n) temp[k++] = a[j++]; for (i = 0; i < k; i++) a[first + i] = temp[i]; } void mergesort(int a[], int first, int last, int temp[]) { if (first < last) { int mid = (first + last) / 2; mergesort(a, first, mid, temp); //左边有序 mergesort(a, mid + 1, last, temp); //右边有序 mergearray(a, first, mid, last, temp); //再将二个有序数列合并 } } int main() { int a[] = {0,2,1,6,3,7,4,5,8}; int len = sizeof(a)/sizeof(int); int * tmp = new int[len]; if(tmp==NULL) return 1; mergesort(a,0,len-1,tmp); for(int i =0;i<len;++i) cout<<a[i]<<" "; cout<<endl; delete[] tmp; return 0; }
归并排序效果图

二叉堆的定义
二叉堆是完全二叉树或者是近似完全二叉树。
二叉堆满足二个特性:
1.父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
2.每个结点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)。
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆:

由于其它几种堆(二项式堆,斐波纳契堆等)用的较少,一般将二叉堆就简称为堆。
堆的存储

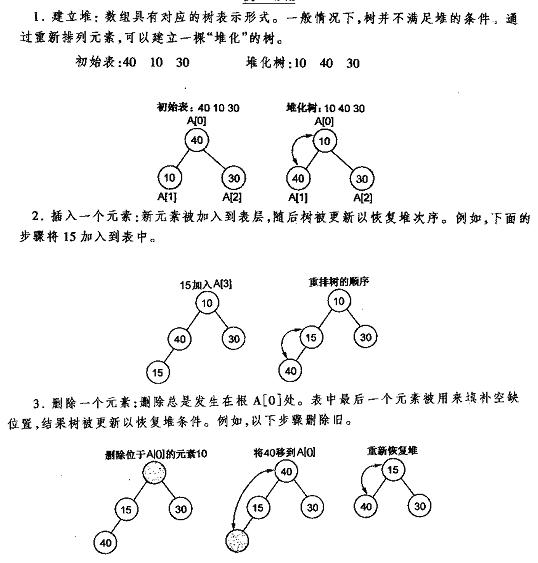
void MinHeapFixup(int a[], int i) { for(int j = (i-1)/2 ; (j>=0&& i!=0)&&(a[i]<a[j]); i= j,j=(j-1)/2) swap(a[i],a[j]); } // 在最小堆中加入新的数据num void MinHeapAddNumber(int a[],int n , int num) { a[n] = num; MinHeapFixup(a,n); }
堆的删除
// 从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2 void MinHeapFixdown(int a[], int i, int n) { int j, temp; temp = a[i]; j = 2 * i + 1; while (j < n) { if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的 j++; if (a[j] >= temp) break; a[i] = a[j]; //把较小的子结点往上移动,替换它的父结点 i = j; j = 2 * i + 1; } a[i] = temp; } //在最小堆中删除数 void MinHeapDeleteNumber(int a[], int n) { Swap(a[0], a[n - 1]); MinHeapFixdown(a, 0, n - 1); }
堆化数组
有了堆的插入和删除后,再考虑下如何对一个数据进行堆化操作。要一个一个的从数组中取出数据来建立堆吧,不用!先看一个数组,如下图:
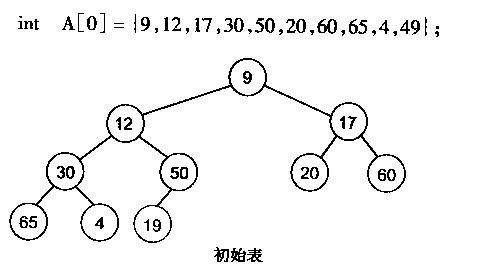
很明显,对叶子结点来说,可以认为它已经是一个合法的堆了即20,60, 65, 4, 49都分别是一个合法的堆。只要从A[4]=50开始向下调整就可以了。
然后再取A[3]=30,A[2] = 17,A[1] = 12,A[0] = 9分别作一次向下调整操作就可以了。下图展示了这些步骤:
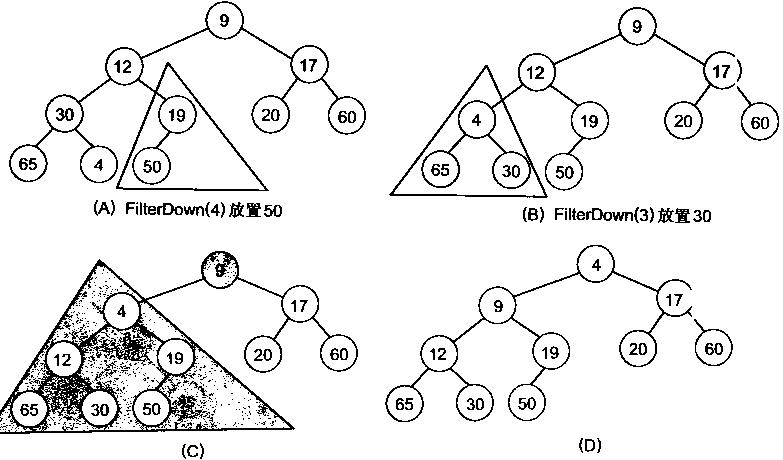
//建立最小堆 void MakeMinHeap(int a[], int n) { for (int i = n / 2 - 1; i >= 0; i--) MinHeapFixdown(a, i, n); }
堆排序
首先可以看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。这样堆中第0个数据又是堆中最小的数据,重复上述步骤直至堆中只有一个数据时就直接取出这个数据。
由于堆也是用数组模拟的,故堆化数组后,第一次将A[0]与A[n - 1]交换,再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换,再对A[0…n - 3]重新恢复堆,重复这样的操作直到A[0]与A[1]交换。
由于每次都是将最小的数据并入到后面的有序区间,故操作完成后整个数组就有序了。有点类似于直接选择排序。
void MinheapsortTodescendarray(int a[], int n) { for (int i = n - 1; i >= 1; i--) { Swap(a[i], a[0]); MinHeapFixdown(a, 0, i); } }
#include <iostream> #include <algorithm> using namespace std; void MinHeapFixup(int a[], int i) { for(int j = (i-1)/2 ; (j>=0&& i!=0)&&(a[i]<a[j]); i= j,j=(j-1)/2) swap(a[i],a[j]); } void MinHeapAddNumber(int a[],int n , int num) { a[n] = num; MinHeapFixup(a,n); } void MinHeapFixdown(int a[], int i ,int n){ int j,temp; j = 2*i+1; temp = a[i]; while(j<n) { if(j+1<n && a[j+1]<a[j]) ++j; // find the min of the left and right child if(a[j]>=temp) break; a[i] = a[j]; i = j; j = 2*j+1; } a[i] = temp; } void MinHeapDeleteNumber(int a[], int n) { swap(a[0],a[n]); MinHeapFixdown(a,0,n-1); } void MakeMinHeap(int a[],int n) { for(int i = n/2-1;i>=0;i--) MinHeapFixdown(a,i,n); } void MinHeapSort(int a[],int n) { for(int i = n-1;i>=1;i--) { swap(a[i],a[0]); MinHeapFixdown(a,0,i); } } int main() { int a[] ={0,3,5,6,4,7,8,2,1}; int len = sizeof(a)/sizeof(int); MakeMinHeap(a,len); MinHeapSort(a,len); for(int i = 0; i<len;i++) cout<<a[i]<<" "; cout<<endl; return 0; }
由于每次重新恢复堆的时间复杂度为O(logN),共N - 1次重新恢复堆操作,再加上前面建立堆时N / 2次向下调整,每次调整时间复杂度也为O(logN)。二次操作时间相加还是O(N * logN)。故堆排序的时间复杂度为O(N * logN)





 浙公网安备 33010602011771号
浙公网安备 33010602011771号