C. Even Picture

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <set>
#include <queue>
#include <map>
#include <sstream>
#include <cstdio>
#include <cstring>
#include <numeric>
#include <cmath>
#include <iomanip>
#include <deque>
#include <bitset>
//#include <unordered_set>
//#include <unordered_map>
#define ll              long long
#define pii             pair<int, int>
#define rep(i,a,b)      for(int  i=a;i<=b;i++)
#define dec(i,a,b)      for(int  i=a;i>=b;i--)
#define forn(i, n)      for(int i = 0; i < int(n); i++)
using namespace std;
int dir[4][2] = { { 1,0 },{ 0,1 } ,{ 0,-1 },{ -1,0 } };
const long long INF = 0x7f7f7f7f7f7f7f7f;
const int inf = 0x3f3f3f3f;
const double pi = 3.14159265358979323846;
const double eps = 1e-6;
const int mod = 1e9 + 7;
const int N = 3e3 + 5;
//if(x<0 || x>=r || y<0 || y>=c)

inline ll read()
{
    ll x = 0; bool f = true; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = false; c = getchar(); }
    while (c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
    return f ? x : -x;
}
ll gcd(ll m, ll n)
{
    return n == 0 ? m : gcd(n, m % n);
}
ll lcm(ll m, ll n)
{
    return m * n / gcd(m, n);
}
bool prime(int x) {
    if (x < 2) return false;
    for (int i = 2; i * i <= x; ++i) {
        if (x % i == 0) return false;
    }
    return true;
}
ll qpow(ll m, ll k, ll mod)
{
    ll res = 1, t = m;
    while (k)
    {
        if (k & 1)
            res = res * t % mod;
        t = t * t % mod;
        k >>= 1;
    }
    return res;
}
bool check(string s,string s1)
{
    int cnt = 0;
    forn(i, s.size())
    {
        if (s[i] != s1[i])
            cnt++;
    }
    if (cnt > 1)
        return false;
    return true;
}
int main()
{
    ll n,cnt=0;
    cin >> n;
    cout << 3 * n + 4 << endl;
    cout << "0 0\n" << "1 0" << endl;
    rep(i, 1, n)
    {
        cout << cnt << " " << i << endl;
        cout << cnt + 1 << " " << i << endl;
        cout << cnt + 2 << " " << i << endl;
        cnt++;
    }
    cout << cnt << " " << n + 1 << endl;
    cout << cnt + 1 << " " << n + 1 << endl;
    return 0;
}

 

------------恢复内容开始------------

Leo Jr. draws pictures in his notebook with checkered sheets (that is, each sheet has a regular square grid printed on it). We can assume that the sheets are infinitely large in any direction.

To draw a picture, Leo Jr. colors some of the cells on a sheet gray. He considers the resulting picture beautiful if the following conditions are satisfied:

• The picture is connected, that is, it is possible to get from any gray cell to any other by following a chain of gray cells, with each pair of adjacent cells in the path being neighbours (that is, sharing a side).
• Each gray cell has an even number of gray neighbours.
• There are exactly nn gray cells with all gray neighbours. The number of other gray cells can be arbitrary (but reasonable, so that they can all be listed).

Leo Jr. is now struggling to draw a beautiful picture with a particular choice of nn. Help him, and provide any example of a beautiful picture.

To output cell coordinates in your answer, assume that the sheet is provided with a Cartesian coordinate system such that one of the cells is chosen to be the origin (0,0)(0,0), axes 0x0x and 0y0y are orthogonal and parallel to grid lines, and a unit step along any axis in any direction takes you to a neighbouring cell.

Input

The only line contains a single integer nn (1≤n≤5001≤n≤500) — the number of gray cells with all gray neighbours in a beautiful picture.

Output

In the first line, print a single integer kk — the number of gray cells in your picture. For technical reasons, kk should not exceed 5⋅1055⋅105.

Each of the following kk lines should contain two integers — coordinates of a gray cell in your picture. All listed cells should be distinct, and the picture should satisdfy all the properties listed above. All coordinates should not exceed 109109 by absolute value.

One can show that there exists an answer satisfying all requirements with a small enough kk.

Example

input

Copy

4

output

Copy

12
1 0
2 0
0 1
1 1
2 1
3 1
0 2
1 2
2 2
3 2
1 3
2 3

Note

The answer for the sample is pictured below:

The sample picture was a red herring, it's hard to generalize to work for arbitrary nn. After drawing for a while you may come up with something like this:

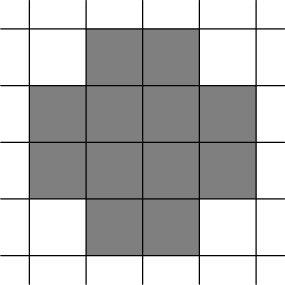
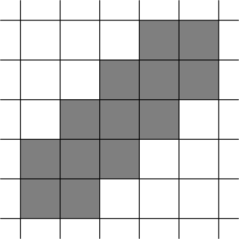
or like this:

------------恢复内容结束------------