B. Filling the Grid

Suppose there is a h×wh×w grid consisting of empty or full cells. Let's make some definitions:

• riri is the number of consecutive full cells connected to the left side in the ii-th row (1≤i≤h1≤i≤h). In particular, ri=0ri=0 if the leftmost cell of the ii-th row is empty.
• cjcj is the number of consecutive full cells connected to the top end in the jj-th column (1≤j≤w1≤j≤w). In particular, cj=0cj=0 if the topmost cell of the jj-th column is empty.

In other words, the ii-th row starts exactly with riri full cells. Similarly, the jj-th column starts exactly with cjcj full cells.

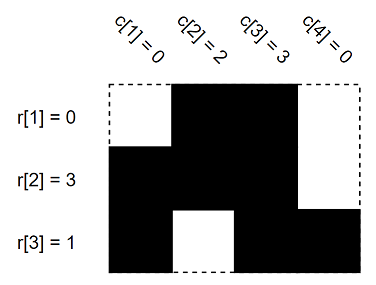These are the rr and cc values of some 3×43×4 grid. Black cells are full and white cells are empty.

You have values of rr and cc. Initially, all cells are empty. Find the number of ways to fill grid cells to satisfy values of rr and cc. Since the answer can be very large, find the answer modulo 1000000007(109+7)1000000007(109+7). In other words, find the remainder after division of the answer by 1000000007(109+7)1000000007(109+7).

Input

The first line contains two integers hh and ww (1≤h,w≤1031≤h,w≤103) — the height and width of the grid.

The second line contains hh integers r1,r2,…,rhr1,r2,…,rh (0≤ri≤w0≤ri≤w) — the values of rr.

The third line contains ww integers c1,c2,…,cwc1,c2,…,cw (0≤cj≤h0≤cj≤h) — the values of cc.

Output

Print the answer modulo 1000000007(109+7)1000000007(109+7).

Examples

input

Copy

3 4
0 3 1
0 2 3 0

output

Copy

2

input

Copy

1 1
0
1

output

Copy

0

input

Copy

19 16
16 16 16 16 15 15 0 5 0 4 9 9 1 4 4 0 8 16 12
6 12 19 15 8 6 19 19 14 6 9 16 10 11 15 4

output

Copy

797922655

Note

In the first example, this is the other possible case.

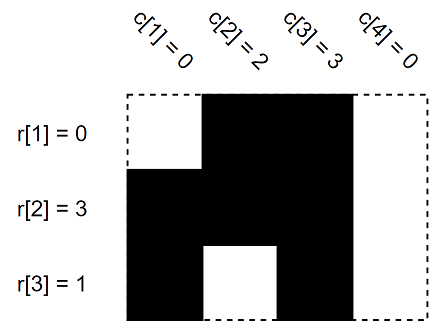
In the second example, it's impossible to make a grid to satisfy such rr, cc values.

In the third example, make sure to print answer modulo (109+7)(109+7).

 

 

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <set>
#include <queue>
#include <map>
#include <sstream>
#include <cstdio>
#include <cstring>
#include <numeric>
#include <cmath>
#include <iomanip>
#include <deque>
#include <bitset>
#include <unordered_set>
#include <unordered_map>
#define ll              long long
#define PII             pair<int, int>
#define rep(i,a,b)      for(int  i=a;i<=b;i++)
#define dec(i,a,b)      for(int  i=a;i>=b;i--)
using namespace std;
int dir[4][2] = { { 0,1 } ,{ 0,-1 },{ 1,0 },{ -1,0 } };
const long long INF = 0x7f7f7f7f7f7f7f7f;
const int inf = 0x3f3f3f3f;
const double pi = 3.14159265358979323846;
const double eps = 1e-6;
const int mod =1e9+7;
const int N = 100005;
//if(x<0 || x>=r || y<0 || y>=c)

inline ll read()
{
    ll x = 0; bool f = true; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = false; c = getchar(); }
    while (c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
    return f ? x : -x;
}
ll gcd(ll m, ll n)
{
    return n == 0 ? m : gcd(n, m % n);
}
ll lcm(ll m, ll n)
{
    return m * n / gcd(m, n);
}
ll qpow(ll m, ll k, ll mod)
{
    ll res = 1, t = m;
    while (k)
    {
        if (k & 1)
            res = res * t % mod;
        t = t * t % mod;
        k >>= 1;
    }
    return res;
}       

int main()
{
    ll h, w;
    cin >> h >> w;
    vector<int> a(h), b(w);
    for (auto& x : a)
        cin >> x;
    for (auto& x : b)
        cin >> x;
    ll cnt = 0;
    for (int i = 0; i < h; i++)
    {
        for (int j = 0; j < w; j++)
        {
            if ((j < a[i] && i == b[j]) || (j == a[i] && i < b[j]))
            {
                cout << 0 << endl;
                return 0;
            }
            if (j - a[i] > 0 && i - b[j] > 0)
                cnt++;
        }
    }
    ll res = qpow(2, cnt, mod);
    cout << res << endl;
    return 0;
}