Pipes

You are given a system of pipes. It consists of two rows, each row consists of nn pipes. The top left pipe has the coordinates (1,1)(1,1) and the bottom right — (2,n)(2,n).

There are six types of pipes: two types of straight pipes and four types of curved pipes. Here are the examples of all six types:

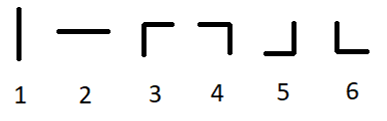Types of pipes

You can turn each of the given pipes 9090 degrees clockwise or counterclockwise arbitrary (possibly, zero) number of times (so the types 11 and 22 can become each other and types 3,4,5,63,4,5,6 can become each other).

You want to turn some pipes in a way that the water flow can start at (1,0)(1,0) (to the left of the top left pipe), move to the pipe at (1,1)(1,1), flow somehow by connected pipes to the pipe at (2,n)(2,n) and flow right to (2,n+1)(2,n+1).

Pipes are connected if they are adjacent in the system and their ends are connected. Here are examples of connected pipes:

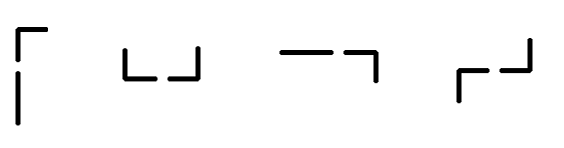Examples of connected pipes

Let's describe the problem using some example:

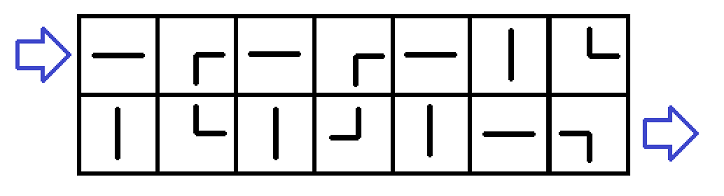The first example input

And its solution is below:

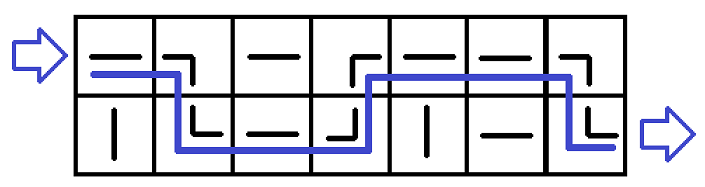The first example answer

As you can see, the water flow is the poorly drawn blue line. To obtain the answer, we need to turn the pipe at (1,2)(1,2) 9090 degrees clockwise, the pipe at (2,3)(2,3) 9090 degrees, the pipe at (1,6)(1,6) 9090 degrees, the pipe at (1,7)(1,7) 180180 degrees and the pipe at (2,7)(2,7) 180180 degrees. Then the flow of water can reach (2,n+1)(2,n+1) from (1,0)(1,0).

You have to answer qq independent queries.

Input

The first line of the input contains one integer qq (1≤q≤1041≤q≤104) — the number of queries. Then qq queries follow.

Each query consists of exactly three lines. The first line of the query contains one integer nn (1≤n≤2⋅1051≤n≤2⋅105) — the number of pipes in each row. The next two lines contain a description of the first and the second rows correspondingly. Each row description consists of nn digits from 11 to 66 without any whitespaces between them, each digit corresponds to the type of pipe in the corresponding cell. See the problem statement to understand which digits correspond to which types of pipes.

It is guaranteed that the sum of nn over all queries does not exceed 2⋅1052⋅105.

Output

For the ii-th query print the answer for it — "YES" (without quotes) if it is possible to turn some pipes in a way that the water flow can reach (2,n+1)(2,n+1) from (1,0)(1,0), and "NO" otherwise.

Example

input

Copy

6
7
2323216
1615124
1
3
4
2
13
24
2
12
34
3
536
345
2
46
54

output

Copy

YES
YES
YES
NO
YES
NO

Note

The first query from the example is described in the problem statement.

 

 简单模拟

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <set>
#include <queue>
#include <map>
#include <sstream>
#include <cstdio>
#include <cstring>
#include <numeric>
#include <cmath>
#include <unordered_set>
#include <unordered_map>
//#include <xfunctional>
#define ll long long
#define mod 1000000007
using namespace std;
int dir[4][2] = { {0,1},{0,-1},{-1,0},{1,0} };
const long long INF = 0x7f7f7f7f7f7f7f7f;
const int inf = 0x3f3f3f3f;

int main()
{
    int q;
    cin >> q;
    while (q--)
    {
        int n;
        cin >> n;
        string a, b;
        cin >> a >> b;
        int level = 1,flag=0;
        for (int i = 0; i < a.size(); i++)
        {
            if (a[i] >= '3' && level==1)
            {
                if (b[i] >= '3')
                    level--;
                else
                {
                    flag = 1;
                    break;
                }
                continue;
            }
            if (b[i] >= '3' && level == 0)
            {
                if (a[i] >= '3')
                    level++;
                else
                {
                    flag = 1;
                    break;
                }
            }
        }
        if (flag || level!=0)
            cout << "NO" << endl;
        else
            cout << "YES" << endl;
    }
    return 0;
}