JOI 2021 Final 做题记录

T1 「JOI 2021 Final」有趣的家庭菜园 4

显然我们先求\(A\)数组的差分

那么显然最后就是要让一段前缀的差分\(>0\)，剩下的\(<0\)

不难发现一个操作是让至多一个差分\(+1\)，至多一个差分\(-1\)

于是枚举波峰算两侧所需次数的\(max\)即可

code

T2 「JOI 2021 Final」雪球

显然每个雪球的覆盖雪的范围是一段包含自己但不会超过他上一个/下一个点的区间

直接记录前缀最大/小值就能二分出区间的左右端点了

显然可以\(O(nlogn)\)但是懒人就是要\(O(nlog^2n)\)

code

T3 「JOI 2021 Final」集体照

注意到关键的条件就是所有人的身高构成排列

于是最后的状态里

必然存在\(T\)个区间\([l_1,r_1],[l_2,r_2]....[l_T,r_T]\)

满足\(l_i=r_{i-1}+1\)

且\([l_i,r_i]\)里填的数恰好是\(r_i\)到\(l_i\)依次递减

考虑一种最终的状态\(b[1..n]\)的贡献

假设原来的\(i\)在\(p_i\)位置

那么次数就是\(\sum_{i=1}^{n} \sum_{j=i+1}^{n} (p_{b[i]}>p_{b[j]})\)

于是设\(f[i]\)表示以\(i\)为某个区间结尾的最小代价

转移就枚举最后一个区间的长度，用树状数组转移即可

code

T4「JOI 2021 Final」机器人

不难发现如果我们想要通过一条边只有两种选择

\(1\)、把他的颜色换成一种新的颜色

\(2\)、把所有和他颜色相同的换成一种新的颜色

于是建边为两者的最小值dijkstra即可

发现有一种特殊情况

就是我们连续走过两条边，在上面分别用\(1\)和\(2\)操作，如果两次操作的边颜色相同，不难发现这样算会多算一次第一条边的贡献

于是我们对于每条边拆出一个点，\((u,v,c,p)\)就拆出\((v,c)\)这个点

抄张图

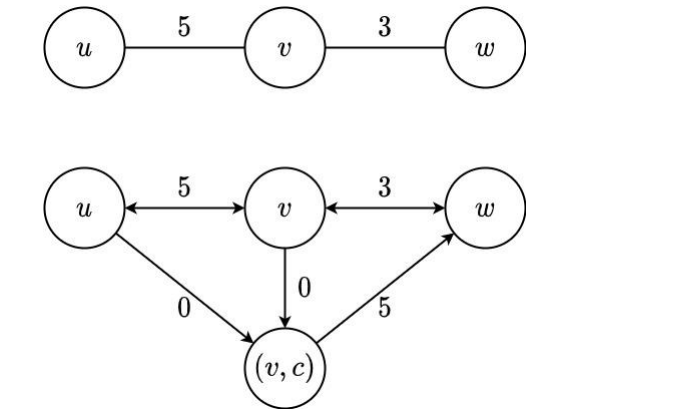
设\((u,0)\)为原图中的\(u\)这个点

把\((u,0)->(v,c)\)连费用为\(0\)的边

\((v,c)\)向所有\(v\)能通过颜色\(c\)到的点连上那条边只有\(2\)操作的权值

不难发现\((u,0)->(v,0)->(w,0)\)先\(1\)再\(2\)且颜色相同就变成了

\((u,0)->(v,c)->(w,0)\)

答案就算对了，并且不会增加新的转移方式

code

T5「JOI 2021 Final」地牢 3

不难想到一个贪心策略

我们考虑当前位置的\(i\)下一个比我这里加能量便宜的位置\(j\)

如果\(i\)到\(j\)的距离是\(d\)，那么把能量加到\(min(u,d)\)显然最优

于是我们就得到一个\(O(nq)\)的优秀做法

考虑优化它

先考虑\(sub3\)的情况，所有的\(T\)都是\(n+1\)

我们考虑离线按左端点\(S\)从大到小离线处理

我们维护一棵线段树下标\(i\)就表示最大容量是\(i\)时的答案

我们考虑左端点左移了\(1\)个单位的改变

维护一个从左到右递减的单调栈

当我们弹出栈顶时我们发现，如果我们的\(U\)大于栈顶到当前的左端点的距离\(L\)的话

我们显然在当前位置会多加一些能量（原来加能量一定会加满到刚好到在那个位置）来替换更劣的价格

于是我们会给\(U\)以后的减去一个折线，来扣掉那部分的贡献

具体而言设当前左端点到栈顶的下一个位置的距离是\(L1\)

那么对于一个大于\(U\)的位置\(x\)，他会减去\((min(x, L1) - L) \times\)栈顶加能量的代价

那么最后我们肯定是要把当前买能量的贡献加上

具体而言设当前位置到栈顶的距离是\(L\)

那么任意一个位置\(x\)，他会加上\(min(x,L) \times\)当前加能量的代价

为了卡常更好写，我们显然可以用两个树状数组代替线段树

接下来考虑\(sub4\)

对于区间\(S\)到\(T-1\)，我们找到距离\(T\)小于等于\(U\)的位置里，代价最小的点\(mid\)

我们发现不管是从\(S\)到\(T\)还是\(S\)到\(n+1\)，我们都一定会在\(mid\)这里加油

简单推导不难发现\(ans(S,T)=ans(S,n+1)-ans(mid,n+1)+(mid到T的距离 \times mid这里加油的代价)\)

于是就转化成了\(sub3\)的问题

code