带花树算法学习笔记

带花树算法大概就是解决一般图的最大匹配

回顾匈牙利算法解决二分图匹配

我们每次增广左侧的a，其实是找到与它有边相连的右侧的一个点b

看b是否在匹配中，如果不在那么增广成功

如果在那么就增广b的匹配点c看是否成功

但我们发现这是因为我们把点集分成两个内部无交的点集才可以这么做

但是对于一般图是不满足这一性质的

这会导致增广时原有的两半边点集可能出现内部匹配

我们需要对匈牙利算法进行改造

看论文得知

其实问题就是出在一般图会有奇环上

我们发现二分图是没有奇环的所以可以直接搞

偷了张图

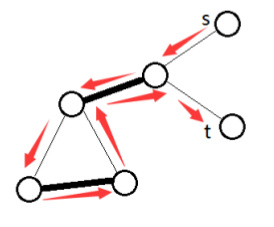
这样匈牙利就会挂掉

于是我们考虑单独搞基奇环

考虑一个长度为(2k+1)的奇环我们可以任意调整匹配

使得出现k对匹配和一个孤立点向外连边，而这个孤立点是可以随意选取的

于是我们可以考虑把奇环缩成一个点是等价的

使用并查集实现

事实上实现我讲不清楚就贴个链接溜了

yyb的博客

我的板子

例题

[WC2016]挑战NPC

把每个篮子拆成三个点，每个球向可以放入的篮子的拆出来的每个点连边

篮子拆出来的点两两连边

做一般图匹配

这样我们发现

一个篮子拆出来点贡献的总匹配数-点匹配的球个数就是我们要求的答案

于是上带花树板子就ok了

code

2020牛客暑期多校训练营第一场 1 or 2

题目

考虑把一个度数为x的点拆成x个点

那么图中的一条边就相当于两端的点可以一遍选一个匹配

两个点拆出的点两两连边即可

但是两个点度数都是2会出问题

可能出现两组匹配这种不合法的情况

于是我们考虑对连接两个度数为2的边新拆出e,e'两个点

那么设两端点为x,y

则连接以下边即可

(x,e),(x'e)

(y,e'),(y',e')

(e,e')

那么问题转化为判断图中是否存在完美匹配

跑带花树板子即可

code