ATCoder 做题记录
AGC 备忘录
Notes
- Beginner:过于简单因此没进备忘录的题
- Easy:能在几分钟内秒掉或者一眼看出了做法的题
- Medium:自己想出了正解或大部分思路的题,或一些正解不难但很有迷惑性的题。
- Hard:自己只想到了个大方向或者束手无策的题
- Insane:完全想不到,几乎理解不能的题
- 加号:该难度中相对难的题。
- 减号:该难度中相对简单的题。
- 前一个难度的加号约等于后面一个难度的减号,用于区分个人差。
AGC001
D (Easy)
一段长度为 \(i\) 的回文事实上就是限制了 \((1,i),(2,i-1),(3,i-2)\) 这样的字符必须相同。
注意到一段长度为 \(L\) 的区间会给这个序列加 \(\lfloor\frac{L}{2}\rfloor\) 个限制,而我们至少需要 \(n-1\) 个限制,所以显然 \(n\) 是奇数就一次都不能浪费,也就是 \(a,b\) 都只能有一个长度为奇数的段了。
然后如果 \(n\) 是偶数我们就可以浪费一次,所以可以分为 \(a\) 有 \(0\) 或 \(2\) 个长度为奇数的。
一个非常强的构造策略是我先输出一个 \(1\),然后全部复读,不难发现这样对于偶数就是合法的,但是错了一位,把错的那位放到开头末尾和奇数的段即可。
E (Easy+)
组合意义。
从 \((-x,-y)\) 走到 \((z,w)\) 的合法路径数就是 \(\binom{x+y+z+w}{x+z}\)。
因此我们直接把走到起点的路径数设为 \(1\) 然后递推一遍,在所有终点处统计贡献。
这样求出的是 \(\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}f(i,j)\),不要忘记稍微处理一下。
F (Hard)
考虑排列中值为 \(i\) 的位置为 \(a_i\)。
那么我们能交换 \(a_i\) 和 \(a_{i+1}\) 当且仅当 \(|a_i-a_{i+1}|\geq k\)。
于是我们发现,如果 \(|a_i-a_j|<k\),无论怎么样它们都不能被交换,也就是说它们的关系已经被固定。
大胆猜测固定所有 \(|a_i-a_j|<k\) 的对同样是构造排列的充分条件,同样可以证明。
因此我们转化回去,就变成了给一个序列,差 \(<k\) 的下标的相对关系已经固定,求可能的最小排列。
这个东西就可以建 DAG 了(然后这里粉兔说明了一些题解的问题)。
于是一个点的入度就是 \(a_{i-k}\sim a_{i+k}\) 里面比它大的数的数量,直接暴力上数据结构即可。
AGC002
D (Easy)
整体二分基础练习题。
E (Medium)
考虑把博弈的网格画出来,然后找到一个厉害的结论:一个点和它左下的胜负态相同。
然后直接搞一下就做完了。
F (Hard)
\(f_{i,j}\) 为放 \(i\) 个白球后放完 \(j\) 种其它颜色球的方案数。
然后每次可以在最前面放一个白球或者在后面的位置随便放 \((k-1)\) 个同一种颜色的新球。
注意 \(i\geq j\)。
AGC003
D (Medium)
非正解。
首先有个 \(O(nv^\frac{1}{3}+n\frac{\sqrt v}{\log v})\) 的做法,过不去。
然后换成 \(O(nv^\frac{1}{3}+nv^\frac{1}{4})\),就过去了。
你不想写 pollard-rho,于是你发现两个数都大于 \(\sqrt v\) 的匹配其实巨少,直接跑到 \(5\) 秒把剩下的都当没匹配直接加进答案里就过了。
E (Medium)
首先离线一下操作,显然如果两个操作有 \(a_i\geq a_{i+1}\) 那 \(a_i\) 就没用了,于是我们可以把 \(a_i\) 转成递增的。
设 \(f(n)\) 为前 \(n\) 个元素的贡献,显然我们可以找到 \(<n\) 且最大的 \(a_i\),记这个东西的值为 \(x\),就可以将 \(f(n)\) 拆成若干个 \(f(x)\) 和一个 \(f(n\text{ mod }x)\) 了。
时间复杂度 \(O(n\log n)\),因为 \(\text{mod}\) 函数每次至少减半。
F (Hard)
因为题目是一个递归的形式,我们尝试现在 \(2\) 层递归中找规律。
我们发现在两个复制的交界处一定是上下交界或者左右交界。
于是考虑交界能否有交:显然在原图上有交的话,在每一层都会有交,反之亦然。
那么枚举一些情况:
- 上下左右都没有交,显然每次连通块都一分为黑格数量个,答案为 \(cnt^{k-1}\),其中 \(cnt\) 为黑格数量。
- 上下左右都有交,显然每次递归完后都仍然联通,答案为 \(1\)。
- 只有上下有交或只有左右有交,下面描述如何处理。
首先如果只有上下有交我们直接旋转 \(90\) 度,这样就只有左右有交了。
然后我们发现,在 \(2\) 层递归的图中,只要原图里有两个相邻的黑格,答案就会减 \(1\),初始答案为 \(cnt^2\)。
类似地,我们只需要求出在 \(k\) 层递归图中有多少相邻的黑格就可以算了。
这是一个简单的问题,直接矩阵快速幂就做完了。
AGC004
D (Easy)
注意到 \(1\) 必须是自环。
然后 \(1\) 肯定在基环树上。
于是把 \(1\) 拆掉之后就是一棵树了,随便做。
E (Hard)
首先让所有机器人移动的细节非常多,我们考虑只让出口移动。
假设出口的移动范围为一个矩形 \(\{i,j,k,l\}\)。
这样的话出口对应的矩形和原矩形就会有一个交,这个交外面的格子要么已经被收集了要么一定白给了,所以这个东西可以作为一个 dp 状态。
我们设 \(f_{i,j,k,l}\) 为这个移动范围下已经被收集或白给的格子中,最多被收集的数量,每次转移即可。
F (Hard)
考虑树的情况。
如果我们把奇数层的节点染黑,一次移动就等价于把两个不同色相邻节点翻转,也就是移动一步黑色节点。
于是问题变成了奇数层有一些节点,每次可以移动一个,问多少次才能使所有白色节点变黑。
考虑每条边的贡献即可。
然后套一个环直接考虑断环为链。
如果是偶环我们依旧枚举某条边贡献,可以发现是一个经典模型。
最后说一下卡了我很久的奇环:这条边的操作一定让黑点 \(+2\) 或者 \(-2\),显然黑白点相等后就不会再操作,所以直接加权值即可。
AGC005
D (Hard-)
考虑钦定 \(i\) 个点不合法,但是仍然满足是一个排列的方案数。
我们发现给同行同列不合法的点连边之后一定是若干条链,求链上独立集。
于是就非常好做了。
E (Hard)
记先手在 A 树上走,后手在 B 树上走。
首先发现一个结论:如果存在两个 A 树上相邻的点在 B 树上的距离 \(\geq 3\),并且先手能走到那个节点,那么答案就是 \(-1\)。
假设不存在上面那类边,也就是说 A 树的边在 B 树上的边的长度 \(\leq 2\),这样我们发现是必然走不出这个子树的,直接 dfs 所有能走到的点,对答案取最大值即可。
F (Medium+)
考虑计算每个点算的次数,其实就是 \(\binom{n}{k}-\sum\limits_{i\in e_x}\binom{sz_i}{k}\)。
于是我们只需要对 \(k=1,2,\cdots,n\) 求出 \(\sum\limits_{i=1}^nc_i\binom{i}{k}\) 即可,显然 \(c_i\) 直接一遍 dfs 就可以求了。
于是推推式子:
就做完了。
AGC006
C (Easy)
不难发现只需要维护坐标期望即可,真实坐标没啥用。
然后坐标期望是非常好算的,我们可以获得一个 \(O(nm)\) 做法。
然后发现 \(n\) 次操作后相当于期望值乘上了一个排列。
于是直接倍增即可,时间复杂度 \(O(n\log m)\)。
D (Medium)
首先二分。
二分完之后,我们发现如果有两个相邻数都是 \(1\) 或 \(0\) 的,它们一定能一起上升到上一行。
于是求出包含中间的一段最小稳定段分类讨论即可。
E (Medium)
首先可以把每一列抽象成它最后的位置和它当前的正反。
一次操作可以看成交换 \(a_x\) 和 \(a_{x+2}\),并将 \(a_x,a_{x+1},a_{x+2}\) 都反过来。
于是我们求出奇偶数位置的逆序对数和初始状态中被反过来的对数。
确认奇偶性即可。
F (Medium+)
这个题看起来巨大像图论题,我们考虑转化成图论,也就是对于任意黑格 \((x,y)\),从 \(x\) 向 \(y\) 连有向边。
如果 \((x,y)\) 变黑了,那么一定存在 \((y,a),(a,x)\) 使得它们都是黑的,于是我们可以把一条正向边转化成两条反向边,又可以把一条反向边转化成两条正向边。
这样可以怎么建模呢?我们考虑把正向边看作 \(+1\),反向边看作 \(-1\),这样模 \(3\) 意义下就对了。
现在我们把边拆成 \(+1\) 和 \(-1\) 的两条,要求任意两个点是否可以走 \(sum\) 模 \(3\) 等于 \(1\) 的边到达。
注意如果边都是一个集合连另一个集合是不可能生成新的边的,要判掉。
AGC007
C (Hard-)
你需要观察到一点:在推掉其中一个球之后,剩下球和盒子的距离的期望仍然是等差数列!
于是就做完了。
这也太神仙了吧?
D (Easy+)
最后方案一定是割成若干段,每次先走到一段的最右边,再走回最左边,再走到最右边。
然后直接优化一下决策点记录一下历史状态就好了。
注意一些很小的细节。
E (Medium+)
首先我们发现是求一个 dfs 序。
如果确定好 dfs 序之后怎么做呢?
我们可以用一个 dp 统计答案:\(f_i=\max(f_l,f_r,g_{l,1}+g_{r,0}),g_i=(g_{l,0}+w_l,g_{r,1}+w_r)\)。
时间复杂度非常劣,但是我们发现这个东西完全可以二分。
二分之后我们相当于维护了一个合法的集合,去掉被二维偏序的点之后还剩一些较小值递增较大值递减的状态。
这个时候我们发现,合并的时候就可以直接启发式了!我们对于 size 较小的去搞一下,然后证明一下总状态数并不会太多就行。
F (Hard-)
考虑答案一定是选一些字符,这些字符不断向右延伸,出现冲突就新开一列。
我们可以发现它们尽量向右挤是最优的。
于是直接把匹配的位置算出来求每一列会有几次冲突即可。
AGC008
D (Easy)
按照 \((a_i,i)\) 排序,然后每次将最前面有空的数用来垫着。
全部弄完之后再对于剩下的元素做一遍,每次也将最前面有空的数拿来垫着。
最后检查一遍是否合法即可。
E (Medium+)
首先我们把 \(i\to a_i\) 表示成 \(i\) 向 \(a_i\) 连边,形成内向基环森林。
于是构造的排列就必须保证 \(i\) 到 \(a_i\) 的距离 \(\leq 2\) 了。
稍微手玩一下可以得到结论:
-
一个不是自环的连通块一定最后还在一个环中。
-
一棵内向基环树可以分两种情况:只有环,和有环上的点。
-
两个长度相等的环可以结合在一起。
-
一个长度为奇数的环可以自己反一下。
-
一棵内向基环树如果不是一个环,不能和其它树合并。
于是问题变成了两个子问题:
- \(n\) 个点,两个点可以套在一起,有 \(k\) 种方法。
- \(n\) 条线段,每条线段可以选择覆盖 \([i,r]\) 或者 \([(i+1)\%n,(r+1)\%n]\),问方法数。
好像都很水,于是就做完了。
F (Hard)
首先我们知道答案肯定不是每个点最大扩展次数的和,因为会算重。
我们考虑所有算重的方案,显然会存在一个 \(d\) 最小的(也就是说 \(d\) 相同,\(x\) 不同所构成的点集也一定不同),我们就考虑只对于这样的 \((x,d)\) 计数。
然后我们考虑判定一组 \((x,d)\) 是否合法:对于所有和 \(x\) 相邻的节点 \(y\),如果 \((x,d)\) 和 \((y,d-1)\) 相等,那么 \((x,d)\) 不合法,反之合法。
也就是说,合法当且仅当去掉任意一棵子树后,都存在一棵子树的深度 \(\geq d\),即第二深的子树深度 \(\geq d\)。
特别地,覆盖整棵树可能不满足上面的规律,所以我们不统计整棵树对应的点集,在最后 \(+1\) 即可。
于是你把其中的一个 subtask 做完了,接下来考虑只能选其中部分点的情况。
那么其实也就是每个点多了一个下界,重点在于怎么计算这个下界。考虑用别的点替代一定是在某一棵子树里选一个点,然后把这个子树全选完,因此考虑所有有可以选的点的子树,取最小的深度即可得到下界。
AGC009
C (Easy)
考虑平方 dp:\(a_{i}\) 属于集合 \(A/B\),上一个属于另一个集合的是 \(a_j\)。
于是 \(f_{i+1,i,A}\) 等于一段区间的 \(f_{i,j,B}\) 的和,暴力计算这段区间即可。
注意有些时候因为 \(a_{i+1}-a_i<A\) 一个前缀都会变成 \(0\),需要处理一下。
D (Hard)
就是点分治,问分治最少层数。
我们发现答案显然 \(\leq \log n\),考虑 \(O(n\log n)\) 的 dp。
考虑点分树的一个描述:点分树上深度相同的点的路径肯定经过一个深度更小的点。
这个描述非常友好:我们发现如果我们将一些点的深度 \(+1\),这一点仍然满足。
于是我们依次枚举并判断即可。
E (Medium)
首先我们考虑每个数对答案的贡献,就是 \(a_i\times\frac{1}{k}^{t_i}\),其中 \(t_i\) 是这个数被操作的次数。
我们发现一个事实:我们可以构造出任意一组 \(\sum \frac{1}{k}^{t_i}=1\) 对应的操作序列!
于是问题变为了找若干个符合要求的小数,直接 dp 即可。
感觉这题反而没有 D 难,为啥洛谷上是黑的啊。
AGC010
D (Easy)
对于 \(n\leq 2\) 特判。
然后你发现如果在不能改变数的奇偶性的情况下答案和所有数减 \(1\) 的和的奇偶性有关。
也就是说一个人如果发现他要输了,必须想个办法使得 \(\gcd\) 是偶数,即所有数都是偶数。
这显然等价于场上只剩下一个 \(>1\) 的奇数且没有 \(1\),此时他的操作也唯一,因此世界线收束。
迭代不会超过 \(\log n\) 轮,因此时间复杂度 \(O(n\log n\log a)\)。
E (Hard)
显然如果两个数不互质那么它们的相对位置就固定了。
首先我们考虑先手确定了这张图。
那么后手只要不断取出 \(deg=0\) 的点中编号最大的点即可。
于是先手反过来使得每个连通块这么做的字典序最小就是最优解。
时间复杂度 \(O(n^2\log a)\)。
F (Medium+)
现在假设先手从 \(1\) 挪到 \(x\)。如果后手在 \(x\) 这棵子树必败,那么它走回去之后先手可以再挪回来,因此后手必败。
唯一的问题是如果 \(a_1\leq a_x\),会出现 \(1\) 先变不合法的情况,此时不能走这个分支,而其它情况都是可以的。
于是我们成功地把判断一个点是否必败分解到它的子树是否必败,对于每个节点 dfs 计算一次即可。
时间复杂度 \(O(n^2)\)。
AGC011
D (Easy+)
手玩一下发现如果第一个墙激活了就会直接被弹回来,不然就可以走到第二个墙的右边,此时第二个墙又被激活,不断重复后就走到了另一侧。
然后对于走到另一侧的情况,对于每个墙,如果下一个墙一开始是激活的那么这个墙一定变成非激活,如果下一个墙一开始是非激活的那么这个墙一定被激活,而最后一个墙一定被激活。
也就是说我们要执行这样的操作:循环右移一位并取反所有数,将开头的 \(1\) 变成 \(0\)。
不难发现这个操作一定以 \(2n\) 为循环节,直接暴力 \(O(n)\) 做就行了。
注意 \(k<2n\) 的步不一定在循环里,需要暴力做。
E (Medium)
可以发现其实一个上升数就是九个形如 \(111\cdots1\) 的数的和。
然而 \(111\cdots 1\) 并没有什么优美的形式,我们考虑整体乘 \(9\)。
于是一个上升数就是九个形如 \(10^x-1\) 的数的和。
也就是说, 我们要求出 \(x\) 至少要表示成多少个形如 \(10^x-1\) 的数的和。
注意到这个答案一定不会很大(最多为 \(9\log x\))我们可以直接从小到大枚举并判断。
于是我们只要支持高精度位数和和加 \(1\) 即可,时间复杂度 \(O(n\log x)\)。
F (Hard+)
照抄 command_block 了,因为实在太过神仙。
显然因为 \(k\) 个时刻会发一辆新车,所以所有车通过轨道的时间都可以对 \(k\) 取模。
设 \(p_i\) 为向右的车在 \(i\) 停靠的时间,\(q_i\) 为向左的车在 \(i\) 停靠的时间。
我们可以列出从左向右的车通过第 \(x\) 个区间的时间为 \(\sum\limits_{i=1}^{x-1}a_i+\sum\limits_{i=0}^{x-1}p_i\sim\sum\limits_{i=1}^{x}a_i+\sum\limits_{i=0}^{x-1}p_i\),而从右向左的车通过第 \(x\) 个区间的时间为 \(-\sum\limits_{i=1}^{x}a_i-\sum\limits_{i=0}^{x-1}q_i\sim-\sum\limits_{i=1}^{x-1}a_i-\sum\limits_{i=0}^{x-1}q_i\)。
如果我们设计的方案合法的话,这个区间是不会有交集的,也就是说这两个集合的交集应该是空的。
稍微整理一下可以得到一个优美的式子:\(\sum\limits_{i=0}^{x-1}p_i+q_i\notin(-2\sum\limits_{i=1}^{x-1}a_i,-2\sum\limits_{i=1}^{x}a_i)\)
做到这个形式之后就非常简单了,每次把这段区间的数放到右边就可以了,可以直接线段树维护 dp。
感觉这题非常困难……准备给后面更困难的题开新等级了。
AGC012
C (Easy)
我们发现如果我们能钦定后一半,那么数量可以转化为前一半符合某种条件的子序列数。
注意到字符集很大,我们尝试构造一个排列。
我们先输出这个排列,再输出一个 \(1\sim n\) 的排列,那么答案就转化为了长度为 \(n\) 的上升子序列数量。
直接倍增构造答案即可。
D (Medium)
考虑这个交换和这个数在哪个位置根本没有关系。
于是如果 \(x,y\) 可以交换,\(y,z\) 可以交换,那么 \(x,y\) 也可以交换,因此我们就可以划分出若干个可以交换的集合,对于每个集合求阶乘即可。
对于每种颜色,同色交换事实上就等价于有一部分数能和 \(w\) 最小的数交换,异色交换就等价于其中一种颜色 \(w\) 最小的能和另一种颜色的一些球交换。
于是剩下的部分是非常平凡的,求出每种颜色内部的集合和颜色之间的连边即可。
E (Medium)
如果你做不出来,一个提示:\(V\) 的值域只有 \(2\times 10^5\)。
不难发现 \(\log V\) 次跳跃之后 \(V\) 一定变为 \(0\),每次跳跃之后能走的都是一个区间。
然后我们就把 \(\frac{1}{2}V,\frac{1}{4}V,\cdots,1\) 分给左边的前缀和右边的后缀,如果存在一种分法就是 possible。
显然我们可以算出使用集合 \(s\) 时最长能覆盖多长的前缀/后缀,唯一的问题是,如果我们对于每个点暴力 check,时间复杂度是 \(O(nV)\) 的。
事实上对于每个长度为 \(V\) 的极长区间的答案都是一样的,而如果极长区间的数量超过了集合中数的数量一定无解,因此时间复杂度降低到 \(O(V\log^2V)\),可以通过。
F (Hard+)
首先我们知道 \(a_i\leq b_i\leq a_{N-i}\)。
设 \(b_i=x\),然后我们知道每次如果我们加两个小于 \(x\) 的数 \(x\) 就会变成 \(x\) 的前驱,加两个大于 \(x\) 的数 \(x\) 就会变成 \(x\) 的后继。
注意到一个数和前后缀之间一定不会相隔其它的数,所以对于任意 \(i>j\),肯定不存在 \(b_i<b_j<b_{i+1}\)。
在这基础上,我们可以证明以上两个条件已经充分,从后往前构造序列即可。
于是在这个结论下,我们可以设计一个从后往前的 dp:\(f_{i,j,k}\) 代表要选 \(i\) 位,前面还有 \(j\) 个数可选,后面还有 \(k\) 个数可选的方案数。
转移是平凡的,时间复杂度 \(O(n^4)\)。
AGC013
D (Easy+)
我们可以把放进去一个红球,拿出来一个蓝球改成放进去一个指定球。
于是我们考虑转化成现在只有 \(n-1\) 个球,做 \(m\) 个放球,拿球的循环(如果先拿球可能存在一些特殊的 case),最后答案乘以 \(2\)。
这样就等价于你可以做 \(m\) 次 \(\pm1,0\) 的操作之后求极差 \(\leq k\) 的操作序列数量。
这个题就比较平凡,先枚举极小值,然后因为 \(n,m\leq 3000\) 的特性直接暴力 dp 转移即可。
E (Easy+)
首先这个 \(\prod a_i^2\) 看起来非常阴间,我们直接大力组合意义拆成在区间里选一个点打一种标记,再选一个点打另一种标记。然后这一切就都好起来了!
记 \(f_{i,0/1,0/1}\) 表示放完前 \(i\) 个,是否打第一种标记,是否打第二种标记,非常好写出转移。
然后如果某个位置被禁了,就代表不能在这个位置新开一段,因为只有 \(10^5\) 个位置,我们直接暴力转移。
时间复杂度 \(O(m\log n)\),常数应该比较大。
F (Hard+)
首先我们都知道对于两个已经确定的序列,只需要检验对于任意一个值 \(v\),\(a\) 序列中 \(\leq v\) 的数的数量都多于 \(b\) 序列中 \(\leq v\) 的数的数量。
于是我们直接转化,就变成了有一个序列和若干区间,每次给一个后缀临时 \(+1\),问至少要选择多少区间 \(+1\) 才能使得每个数 \(\geq 0\)。
我们考虑有没有不依赖于后缀的决策:显然对于一个 \(\leq -2\) 的 \(v\) ,它必须被覆盖到至少 \(-1\)。
然后最后相当于我们只需要覆盖一段前缀的 \(-1\),我们可以对于每个前缀分别求出答案。
特别注意的是,第一遍我们应该从后往前依次处理,不然如果 \(4\) 需要一个区间,我们选了 \([2,6]\),但是如果覆盖了 \(2\) 开始的后缀,最优的方案应该是选 \([1,5]\),这个贪心就错误了。
AGC014
D (Easy)
如果一个点有两个叶子显然木大。
如果一个点有一个叶子显然可以把这个点先选强迫后手选那个叶子,这样就可能产生更多叶子。
直接选择一个非叶子节点 dfs 模拟即可。
E (Easy)
注意最后一次连边,一定是直接一条蓝边换一条红边。
而这次连边之前,显然这条边一定要被保留,所以直接将这两个点合并即可。
代码有一些小细节。
F (Hard)
对于 \(i=1\),显然这个数不会影响别的数是不是前缀最大值。
于是其实我们先求出 \(i=2\sim n\) 的答案,然后再看看这么多次之后是否 \(1\) 也归位了。
显然在 \(i=2\sim n\) 的倒数第二步完成时,此时 \(2\sim n\) 的第一个数显然不是 \(2\)。
我们考虑将第一个数 \(x\) 和 \(1,2\) 的位置关系求出,然后证明一个非常厉害的事情:这三个数相对的循环顺序不会改变。
具体证明基于一个结论: \(x\) 当且仅当在第一个位置时是前缀最大值,其它情况都不是前缀最大值。
于是在最后一步完成时,如果我们在所有操作前的相对顺序是 \(1,2,f\),那么 \(1\) 就自动归位了。不然第一位上的数还是 \(2\),就需要再合并一次。
直接模拟这个过程扫一遍就行了。
AGC015
D (Easy)
考虑不断求包含最高位的数有多少能被表示。
假设现在同时存在有最高位的数和没最高位的数。
不含最高位的数能构造的数显然在 \([l, 2^x)\)。
包含最高位的数构造的数显然在 \([2^x,2^{x}\text{ or }(2^{x}+1)\text{ or }\cdots\text{ or }r)\)
将它们的并集加入答案,并将最高位的数都丢了,分解成子任务。
如果所有数的最高位相同,显然所有能构造的数都包含最高位,减去最高位后分解成子任务即可。
时间复杂度 \(\text{polylog}(r)\)。
E (Medium-)
注意所有点最后一定按照 \(v\) 排序。
对于第 \(i\) 个点,如果有第 \(j\) 个点最开始在 \(i\) 后面,最后在 \(i\) 前面,那么 \([i,j]\) 的所有点显然都在 \(i\) 被初始染色的时候染上色。
于是我们可以算出第 \(i\) 个点的染色区间 \([l,r]\),显然 \([l,r]\) 有单调性,随便 dp 一下就可以了。
F (Hard)
我们要构造答案越大越好,注意到如果 \(x<y\),\((x,y)\) 会变成 \((y\bmod x,x)\),我们直接反向构造,从 \((0,1)\) 开始反推。因为我们要让用的数尽可能小,我们显然会从 \((y,x)\) 推回 \((x+y,x)\)。
最后会发现其实最小的最深答案就形如 \((Fib_i,Fib_{i+1})\),因此答案也只有 \(\log n\) 级别。
考虑哪些数对可能可以这样反向构造回去。显然构造的方法就是不断推回 \((kx+y,x)\)。
不难发现 \(k\) 在除了最后一步的位置只能取 \(1\) 或 \(2\),不然可以证明如果这样存在解则存在一个答案更大的解。同样不难发现的是 \(2\) 只能选一次,证明的方法是类似的。
因此我们还证明了除去最后一层,反向构造在最后一步之前只能构造出层数个解。
于是我们直接对于所有解求出最后一步能得到几个合法对即可。
注意在只有一层的时候特判。
AGC016
D (Not solved)
我们记所有数的异或和为 \(S\),显然每次的操作就是交换 \(a_i\) 和 \(S\)。
我们考虑对于所有 \(a_i\neq b_i\) 的 \((a_i,b_i)\) 连边,对于每条边答案 \(+1\),每个连通块答案 \(+1\)。
最后注意如果存在 \(b_x=\bigoplus\limits_{i=1}^n a_i\),可以省去一次。
E (Medium-)
每只鸡的情况要么是一定死,要么是可能活下来。
如果一只鸡可能活下来,那么一定存在一个集合 \(S\),只有集合 \(S\) 中的鸡全在某次选择中被献祭才可能让最后的某只鸡活下来。
我们可以依次模拟所有操作,如果某次操作为两只都有可能存活的鸡 \((x,y)\),那么 \(y\) 的集合就要或上 \(x\) 的集合,并且 \(x\) 的集合也要并上 \(y\) 的集合。
特别地,如果两个集合交集为空,显然这两只鸡都必死,因为一只鸡没有办法献祭两次。
最后枚举集合判断交集是否为空即可,时间复杂度 \(O(n^3+nm)\)。
F (Medium)
不难扯到 SG 函数上做。
我们考虑直接钦定每个点的 SG 函数,然后要满足以下要求:
- \(sg_i=A\) 的点要对于每个 \(B<A\) 向至少一条 \(sg_j=B\) 的点连边。
- \(sg_i=A\) 的点之间不能连边。
那么我们考虑钦定一个点集是合法的,每次加一个新的点集,加入的点集的 SG 函数都是原点集的 SG 函数最大值 \(+1\)。
再看看要满足什么要求:这些点之间的边全部不取,对于每个集合外的点和新选的点之间的连边要至少选一条边。
可以做到 \(O(n3^n)\)。
AGC017
D (Easy)
经典 SG 函数练习题。
我们尝试表示一棵子树的 SG 函数。
不难发现,如果加入一棵子树,因为子树可以变成任意操作后状态或者直接消失,所以相当于 SG 函数异或上 \(f_y+1\)。
检查 \(f_1\) 是否为 \(0\) 即可。
E (Medium)
讲个笑话,我一直以为可以翻转。
记一个点某侧的权值,接地为 \(-a_i\) 或 \(b_i\),没接地为 \(c_i\) 或 \(-d_i\), 显然两个点能连当且仅当权值相等。
于是大力边转点,我们就要从一个正数点开始,走若干个有向边到负数点。
注意到可以不连成一段,所以可能会走多次。我们建一个超级起点和超级终点,检查是否在增加若干条这两个点之间的边后存在一条欧拉回路即可。
具体来说就是每个正数点出度都不比入度少,负数点同理,并且不能有一个连通块内部消化完了。
F (Medium+)
显然的思路:放完 \(x\) 根线,状态为 \(S\) 的方案数,时间复杂度高达 \(O(4^{n}\text{poly}(nm))\)。
问题在于我们一次枚举了过多的状态,我们尝试分解每层的状态。
考虑放完 \(x\) 根线,第 \(x+1\) 根线覆盖部分方案为 \(A\),未覆盖部分方案为 \(B\),两个状态之间距离为 \(d\)。
时间复杂度为 \(O(2^nn^2m)\),空间复杂度 \(O(2^nn)\),无法通过。
我们发现覆盖的特殊要求就是 \(A\) 的前缀 \(\text{popcount}\) 要大于等于 \(B\) 的前缀 \(\text{popcount}\)。
所以可以不记录到某一位的距离,记录第 \(i\) 条线走完前 \(j\) 步,已经覆盖的位为 \(A\),剩余要覆盖的位为 \(B\) 的方案数即可。
AGC018
D (Easy+)
首先对于哈密顿回路的问题是经典的,就是每条边的边权乘 \(\min(sz_x,sz_y)\)。
对于哈密顿路,显然我们只需要扣掉一条边。
我们考虑哈密顿回路的构造方式,核心就是要每次进入以重心为根的不同子树。
因此我们扣掉一个点只需要扣掉最后回重心的那个点即可,答案只需减去重心的出边中距离最短的那条。
特别注意的是如果有两个重心,那么只有它们之间的边是两个重心的公共出边,特判即可。
E (Not solved)
F (Not solved)
AGC019
D (Not solved)
E (Not solved)
F (Hard-)
显然如果还剩 Yes 多我们就猜 Yes,不然猜 No。
于是我们放到二维平面上,每个决策可以表示成一条边,数所有路径经过的决策边数量之和即可。
唯一的问题是决策边的数量并不好数,是这个形状的:
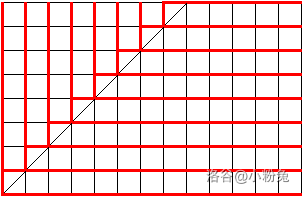
我们考虑把每条边超出斜线的部分强行折回去,然后加上 \(0.5\) 的贡献(因为一定会走一条超出斜线的竖边)。
计算斜线上的每个点被经过的路径条数即可。特别注意因为事实上我们没有折回去,所以计算的其实就是走到左下的路径数量乘以走到右上的路径数量。
AGC020
D (Not solved)
E (Not solved)
F (Not solved)
AGC025
D (Easy+)
对于所有距离为 \(D_1\) 的点连边,可以证明这是一张二分图。
取出点较多的一侧,对于所有距离为 \(D_2\) 的点连边,仍然可以证明这是一张二分图。
因此最终至少可以选出 \(\lceil\frac{\lceil\frac{4n^2}{2}\rceil}{2}\rceil\geq n\) 个点。
E (Hard)
抛出一个结论:所有被经过至少两次的边都能提供 \(2\) 的贡献。
考虑每次选一个叶子。
如果这个叶子没有连向父亲的路径,那么我们什么都不用考虑,直接删点即可。
如果只有一条连向父亲的路径,我们就之后再考虑,将这条路径的起点改为它的父亲。
如果有 \(\geq 2\) 条连向父亲的路径,我们选一条定一个方向,再选一条定反方向,剩下的随意。
设这两条路径的终点分别为 \(a,b\),它们从当前结点 \(x\) 分开的位置为 \(t\),显然 \(x\to t\) 的路径肯定被覆盖两次,而 \(t\to a\) 和 \(t\to b\) 因为方向相反可以变成 \(a\to b\) 的路径。显然因为这个节点是叶子,\(x\) 肯定不等于 \(t\),所以我们成功地将问题缩小到了相同条件的更小规模,反复操作即可。
由于数据范围很小某些地方可以复杂度换码量,然而细节还是很多。
F (Hard-)
每次操作可以看成是从高到低,对于每个都为 \(1\) 的位产生一次进位,并处理随之带来的进位。
我们发现一件神奇的事情:我们可以对于从高到低的位,直接产生至多 \(k\) 次进位,与上述操作等价。
证明可以使用归纳法,在我们增加一次的时候,如果某一位上都是 \(1\), 那么这一位进位之后位置上的数一定是 \(0\)。而即使它下面的所有位都全为 \(1\),这一位也无法继续进位。
此时我们得到了一个 \(O(nk)\) 的暴力,考虑继续优化。
我们发现只有在 \((01,01)\) 的情况下对低位进位不会减小 \(0\) 的个数,于是我们将连续的 \((0,0)\) 段压在一起存之后暴力模拟,时间复杂度即为 \(O(n)\)。
有趣的事实:zhoukangyang 没有使用这个性质也切掉了此题,大家可以膜拜他。
AGC055
A (Easy+)
我觉得比 B 难。
将字符串分成三段,每次枚举一个 ABC 的排列 \(s\),尝试在第 \(i\) 段中找出尽可能多的 \(s_i\),取最小之后将这些字符取出即可。
可以通过一些方式证明最后一定能取完。
B (Easy)
首先我们发现无论怎么操作每种字符的数量都是不变的。
注意到一个性质:如果有一个 ABC,它可以和任意一个字符交换。
于是我们直接对于 \(s,t\) 寻找 ABC 并移到最前面即可。
当没有东西可以移动时能否转换等价于剩下的两个串是否完全相同。
C (Medium-)
一个显然的性质:所有数的答案要么是 \(L-1\),要么是 \(L\),其中 \(L\) 为序列的 LIS 长度。
于是一个很自然的想法是枚举哪些位置是 \(L-1\)。
枚举完哪些位置是 \(L-1\) 之后,我们发现我们要求的就是 \(L\) 的最大值和最小值。
最小值是显然的,也就是 \(L-1\) 的位置数量,构造为剩下的数全选 \(+\infty\),注意要和 \(3\) 取 \(\max\)。
最大值应该是在每个空隙中尽可能塞若干对数。
例如,我们选择 \(\{1,3,6,8\}\),那么我们可以让 \(a_3<a_4=a_5<a_6\),那么这样 LIS 长度就增加了 \(1\),注意 \(0\) 和 \(n+1\) 都必须选上。
不难发现能塞的对数和选的数的数量只和长度为奇数的空隙有关,枚举选的数的数量和长度为奇数的空隙计算即可。
注意选所有数和不选数是两种情况。
D (Hard)
神仙结论题。
记 \(A_x\) 为序列所有前缀 \(A\) 比 \(B\) 多的数量的最大值,\(B_x\) 和 \(C_x\) 的定义类似。
抛出一个神仙结论:序列可以被分解当且仅当 \(A_x+B_x+C_x\leq n\) 且 \(A,B,C\) 各有 \(n\) 个。
必要性显然,充分性也可以通过一些技巧证明。
于是直接大力 dp 就可以了。

