cqyz oj | 扩展欧几里得算法 | Exgcd

Description

　　欧几里德算法又称辗转相除法，是指用于计算两个正整数a，b的最大公约数。应用领域有数学和计算机两个方面。计算公式。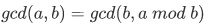

 

 　　扩展欧几里德算法是用来在已知a, b，求解一组 x,y 使得：ax + by = gcd(p,q) (解一定存在，根据数论中的相关定理)。

　　本题任务：给定任意整数a,b,c，求方程 ax + by = c 的整数解，输出其中x是最小的正整数的一组。

Input

　　若干行，每行一组数据：a,b,c。他们都是int范围内的整数。

Output

　　每组数据输出一行，若给定方程没有整数解，输出"No solution"，否则输出x是最小的正整数的一组。

Sample Input 1 

1 1 1
1 2 1000
12 20 7
27 -45 18
6 15 9

Sample Output 1

1 0
2 499
No solution
4 2
4 -1

Hint

a,b,c在int范围内，且都不为0。

---

 

1.理论部分

欧几里得算法求最大公因数：

int gcd(int a, int b) {
    if(b == 0) return a;
    else return gcd(b, a%b);
}

其中模运算可定义为：（以下除法都是指下取整除法）

a%b = a-a/b*b

 

扩展欧几里得算法：已知整数a、b，扩展欧几里得算法可以在求得a、b的最大公约数的同时，能找到整数x、y（其中一个很可能是负数），使它们满足贝祖等式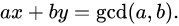

 

推导：由欧几里得算法：

ax + by = g //g=gcd(a,b)
==> bx' + (a%b)y' = g
==> bx' + (a-a/b*b)y' = g
==> bx' + ay' - a/b*by' = g
==> ay' + b(x'-a/b*y') = g
==> x=y',  y=x'-a/b*y'

这样可以迭代求解，通过调用gcd(b, a%b)得到的x'和y'算出当前的x和y

由上述推导可直接写出如下的扩展欧几里得算法：

int Exgcd(int a, int b, int &x, int &y) {
    if(b == 0) { x=1, y=0; return a; } // gcd=a => gcd*1+0*y=a => x=1, y任取 
    int xx, yy;
    int gcd = Exgcd(b, a%b, xx, yy);
    x = yy;
    y = xx - a / b * yy;
    return gcd;
}

可以不用xx和yy，代码稍加化简得到：

int Exgcd(int a, int b, int &x, int &y) {
    if(b == 0) { x=1; return a; }
    int gcd = Exgcd(b, a%b, y, x);
    y = y - a / b * x;
    return gcd;
}

 

通过调用gcd = Exgcd(a, b, x, y)，可得到一组满足ax+by=gcd的x和y的特解。

 

根据裴蜀定理，这样的x,y应该有无数对。

已知一对特解x0,y0，可由如下方式得到通解：

x = x0 + b / gcd * k

y = y0 - a / gcd * k（k属于整数）

证明：将x, y代入方程：

ax + by

= a(x0 + b / gcd * k) + b(y0 - a / gcd * k)

= a*x0 + b*y0 = gcd(a, b)

成立,证毕.

为了找到尽量多的通解，每次转移的步长应该尽量短，故式中a、b要/gcd

 

2.实践部分

利用扩展欧几里得算法实现本题：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;

LL Exgcd(LL a, LL b, LL &x, LL &y) {
    if(b == 0) { x=1, y=0; return a; } // gcd=a => gcd*1+0*y=a => x=1, y任取 
    LL gcd = Exgcd(b, a%b, y, x);
    y = y-a/b*x;
    return gcd;
}

int main() {
    LL a, b, c, x, y, gcd;
    while(scanf("%lld%lld%lld", &a, &b, &c) == 3) {
        gcd = Exgcd(a, b, x, y); // 得到满足ax+by=gcd(a, b)的一组x, y 
        if(c%gcd != 0) { puts("No solution"); continue; }
        a/=gcd, b/=gcd, c/=gcd; // 方程两边约分使得a, b互质gcd=1 
        if(b<0) a=-a, b=-b, c=-c, x=-x, y=-y; // 保证b为正，下面x0求出来才为正 
        // 方程改为(-a)x+(-b)y=(-c)
        // x,y符号不变，但为了使下一步算x0的x*c符号总体不变此处x,y符号改变 
        LL x0 = x*c; // x是ax+by=1的一个x, 所以x0=x*c是ax+by=c的一个x
        x0 = (x0 % b + b) % b; // ax+by=1 的通解: x=x0+k*b , y=y0-k*a， 代入方程展开即证 
        if(x0 == 0) x0 = b; // 保证为最小正整数 
        LL y0 = (c-a*x0)/b; // 确定了x0求y0 
        printf("%d %d\n", (int)x0, (int)y0);
    }
    return 0;
}

-