cqyz oj | 重建道路

Description

　　一场可怕的地震后，人们用N个牲口棚(1≤N≤150，编号1..N)重建了农夫John的牧场。由于人们没有时间建设多余的道路，所以现在从一个牲口棚到另一个牲口棚的道路是惟一的。因此，牧场运输系统可以被构建成一棵树。John想要知道另一次地震会造成多严重的破坏。有些道路一旦被毁坏，就会使一棵含有P(1≤P≤N)个牲口棚的子树和剩余的牲口棚分离，John想知道这些道路的最小数目。 

　　PS：最少需要去掉多少条边才能获得一棵含p个结点的子树。

Input

　　第1行：2个整数，N和P　　第2..N行：每行2个整数I和J，表示节点I是节点J的父节点。

Output

　　单独一行，包含一旦被破坏将分离出恰含P个节点的子树的道路的最小数目。

Sample Input 1 

11 6
1 2
1 3
1 4
1 5
2 6
2 7
2 8
4 9
4 10
4 11

Sample Output 1

2

Hint

1≤N≤150

---

题目给出了一棵有根树，须先要根据输入的信息确定根结点的编号 root。样例画出的树型图如下。

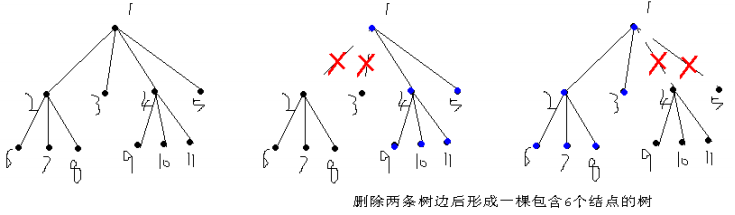
由上面可以看出，针对以 i 为根的树，根 i 有 2 种状态：

状态 0、i 不在要保留的子树中；

状态 1、i 在要保留的子树中；

 

 

所以，可以状态函数的定义如下：

状态函数定义：

𝑓(𝑖, 𝑥, 0)表示以 i 为根的树中，获得一棵 x 个结点的子树（不含 i），最少需要删除多少条边。

𝑓(𝑖, 𝑥, 1)表示以 i 为根的树中，获得一棵 x 个结点的子树（包含 i），最少需要删除多少条边。

 

状态转移方程：

𝑓(𝑖, 𝑥, 0) = min( 𝑓(𝑖, 𝑥, 0)， 𝑓(𝑗, 𝑥, 0)，𝑓(𝑗, 𝑥, 1) + 1 )

𝑓(𝑖, 𝑥, 1) = 𝑚𝑖 𝑛( 𝑚𝑖𝑛* 𝑓(𝑖, 𝑥 − 𝑦, 1) + 𝑓(𝑗, 𝑦, 1) | 1 ≤ 𝑦 ≤ 𝑚𝑖 𝑛(𝑥 − 1, 𝑠𝑧[𝑗])+ ，𝑓(𝑖, 𝑥, 1) + 1)

边界分析： 𝑓(𝑖, 0,0) = 𝑓(𝑖, 1,1) = 0

最后的答案： 𝐴𝑛𝑠 = 𝑚𝑖𝑛(𝑓(𝑟𝑜𝑜𝑡, 𝑃, 0), 𝑓(𝑟𝑜𝑜𝑡,𝑃, 1));

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = 155, inf = 0x3f3f3f3f;

int fir[maxn], ne[maxn*2], to[maxn*2], np;
void add(int x,int y){
    ne[++np] = fir[x];
    fir[x] = np;
    to[np] = y;
}

int n, m;
int fa[maxn];
void data_in(){
    scanf("%d%d", &n, &m);
    for(int i=1, x, y; i<n; i++){
        scanf("%d%d", &y, &x);
        add(fa[x] = y, x);
    }
}

int f[maxn][maxn][2], sz[maxn];
void dp(int u){
    sz[u] = 1;
    f[u][0][0] = f[u][1][1] = 0;
    for(int i=fir[u]; i; i=ne[i]){
        int v = to[i];
        dp(v);
        sz[u] += sz[v];
        for(int x = min(m, sz[u]); x; --x){
            f[u][x][0] = min(f[u][x][0], min(f[v][x][0], f[v][x][1]+1));
            int t = inf;
            for(int y = min(x-1, sz[v]); y; --y)
                t = min(t, f[u][x-y][1] + f[v][y][1]);
            f[u][x][1] = min(t, f[u][x][1]+1);
        }
    }
}

void solve(){
    memset(f, 0x3f, sizeof(f));
    int rt;
    for(int i=1;i<=n;i++)
        if(!fa[i]){
            rt = i;
            break;
        }
    dp(rt);
    printf("%d", min(f[rt][m][0], f[rt][m][1]));
}

int main(){
    data_in();
    solve();
    return 0;
}