猜猜看 (数论)
题面
记 s k = ∑ i = 1 k x i s_k=\sum_{i=1}^kx_i sk=∑i=1kxi
现在你需要求出 ∏ i = k n s i \prod_{i=k}^ns_i ∏i=knsi 展开再合并同类项后有多少项。
答案可能很大,请对 998244353 998244353 998244353 取模。
输入两个数 n , k n,k n,k , 1 ≤ k ≤ n ≤ 100000 1\leq k\leq n\leq100000 1≤k≤n≤100000 ,输出一个数表示答案。
校长 O n e I n D a r k \tt OneInDark OneInDark 说这是道板题,是什么板题呢?猜猜看。
输入:5 3
输出:28
解释:
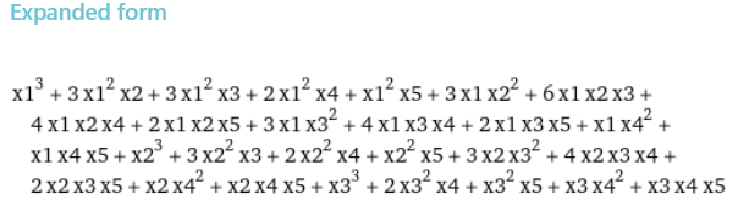
题解
先用一个艰难的转换。
最终的式子,是每个多项式中选一个数乘起来,所有选法相加,我们需要的是去重过后的个数。
我们留意到,有
k
k
k 个变量是所有多项式都可以选的,有
n
−
k
n-k
n−k 个变量分别只有倒数
n
−
k
n-k
n−k 、倒数
n
−
k
−
1
n-k-1
n−k−1、……、最后一个多项式可以选。那么,我们对于每一种选法,把选的变量从右往左叠放:
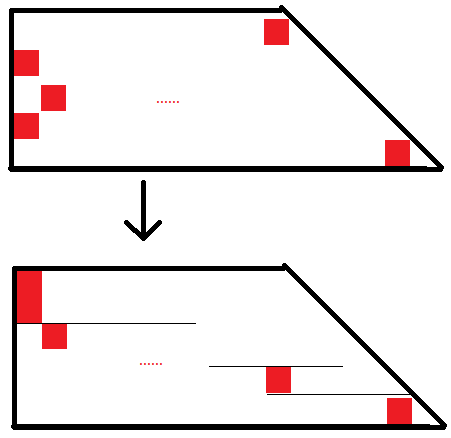
这样就体现出了它的后缀和增长线,我们会发现这个后缀和增长线媲美这样一条折线:
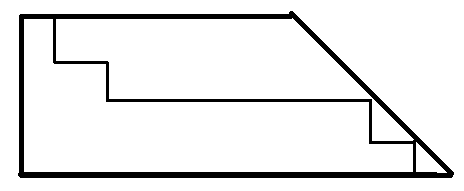
从左上到右下,不越过斜线,只能往右或往下走的方案数!
因此,可以说,这是道卡塔兰数的模板题,根据卡塔兰数的几何推导,答案就是 C ( 2 n − k + 1 , n ) − C ( 2 n − k + 1 , n − k ) C(2n-k+1,n)-C(2n-k+1,n-k) C(2n−k+1,n)−C(2n−k+1,n−k) 。
CODE
#include<set>
#include<map>
#include<stack>
#include<cmath>
#include<ctime>
#include<queue>
#include<vector>
#include<bitset>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 400005
#define LL long long
#define DB double
#define ENDL putchar('\n')
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
#define SI set<PO>::iterator
#define eps (1e-9)
#define SQ 447
LL read() {
LL f=1,x=0;char s = getchar();
while(s < '0' || s > '9') {if(s=='-')f = -f;s = getchar();}
while(s >= '0' && s <= '9') {x=x*10+(s-'0');s = getchar();}
return f*x;
}
void putpos(LL x) {
if(!x) return ;
putpos(x/10); putchar('0'+(x%10));
}
void putnum(LL x) {
if(!x) putchar('0');
else if(x < 0) putchar('-'),putpos(-x);
else putpos(x);
}
const int MOD = 998244353;
int n,m,s,o,k;
int fac[MAXN],inv[MAXN],invf[MAXN];
int C(int n,int m) {
if(m < 0 || m > n) return 0;
return fac[n] *1ll* invf[n-m] % MOD *1ll* invf[m] % MOD;
}
int main() {
// freopen("guess.in","r",stdin);
// freopen("guess.out","w",stdout);
n = read();k = read();
fac[0]=fac[1]=inv[0]=inv[1]=invf[0]=invf[1]=1;
for(int i = 2;i <= n*3;i ++) {
fac[i] = fac[i-1]*1ll*i % MOD;
inv[i] = (MOD-inv[MOD%i]) *1ll* (MOD/i) % MOD;
invf[i] = invf[i-1] *1ll* inv[i] % MOD;
}
int N = n,M = n-k+1;
int ans = (C(N+M,N) +MOD- C(N+M,M-1)) % MOD;
printf("%d\n",ans);
return 0;
}


